Содержание
- 2. Содержание: Цель и задачи Введение Понятие секущей плоскости и определение сечения многогранника Основные аксиомы и теоремы,
- 3. Сформировать умения у учащихся строить сечения тетраэдра и параллелепипеда заданной плоскостью. Дать определение секущей плоскости и
- 4. Вспомним сказку “Маленький принц”. Помните, какую картинку (первую в своей жизни) нарисовал в детстве Экзюпери? Посмотрите
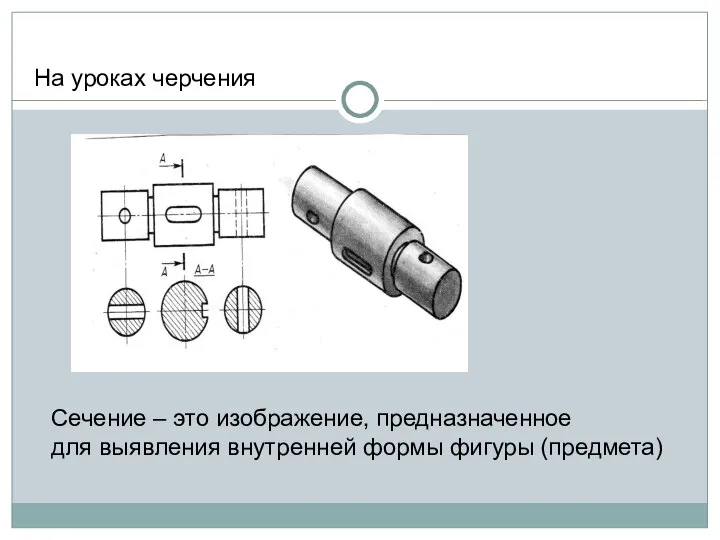
- 5. На уроках черчения Сечение – это изображение, предназначенное для выявления внутренней формы фигуры (предмета)
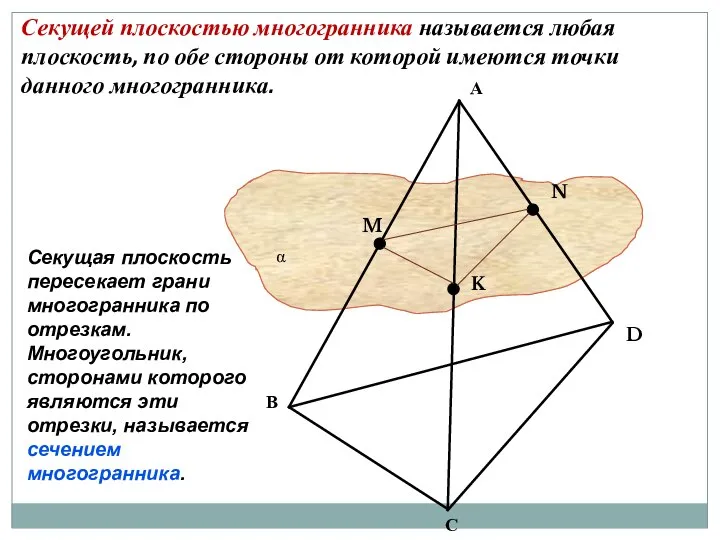
- 6. Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая
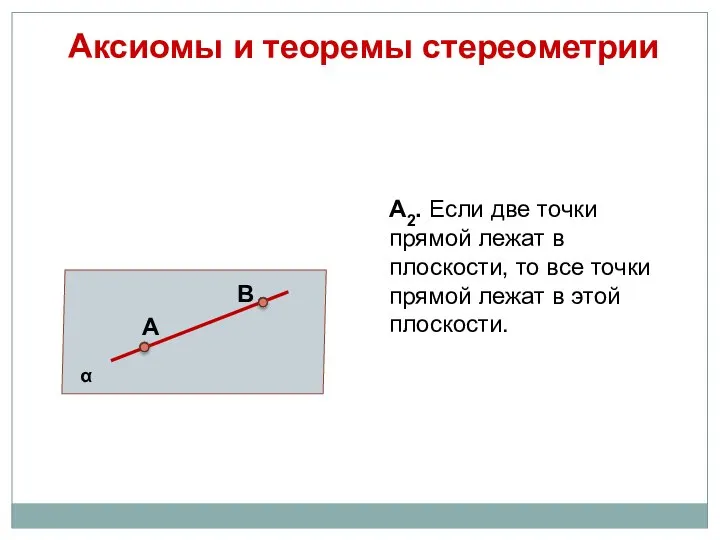
- 7. Аксиомы и теоремы стереометрии А2. Если две точки прямой лежат в плоскости, то все точки прямой
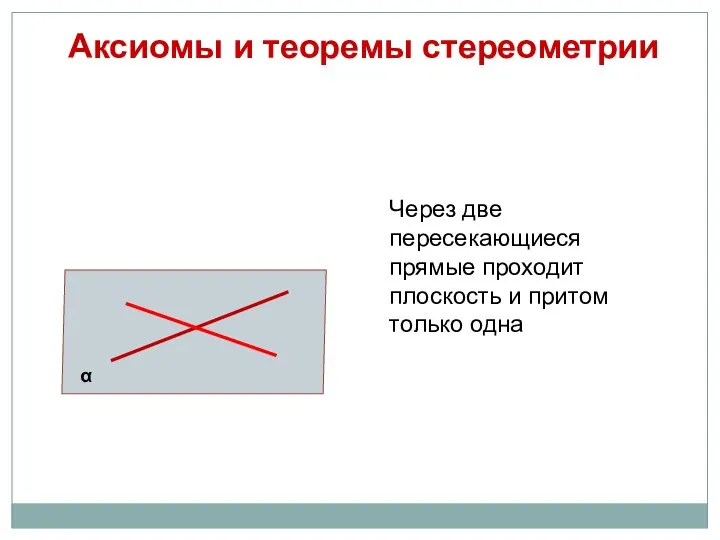
- 8. Аксиомы и теоремы стереометрии Через две пересекающиеся прямые проходит плоскость и притом только одна α
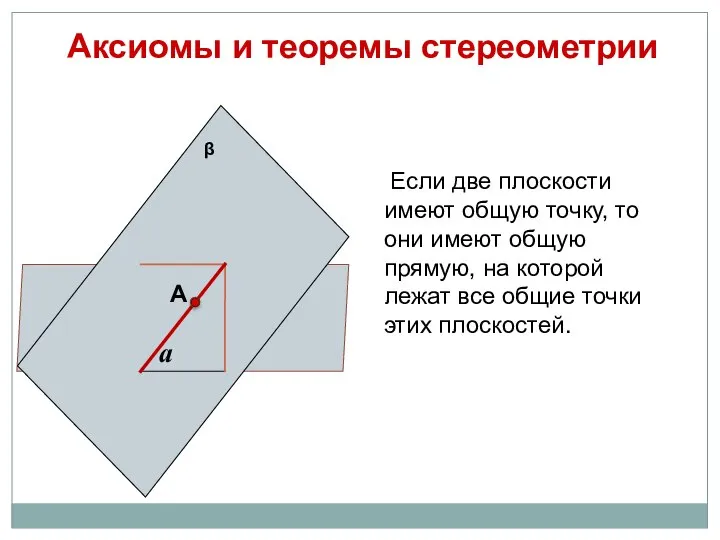
- 9. Аксиомы и теоремы стереометрии Если две плоскости имеют общую точку, то они имеют общую прямую, на
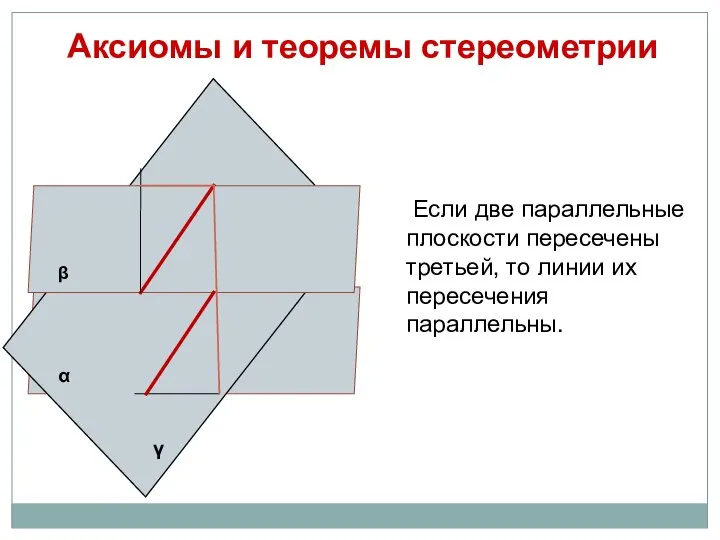
- 10. Аксиомы и теоремы стереометрии Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. α
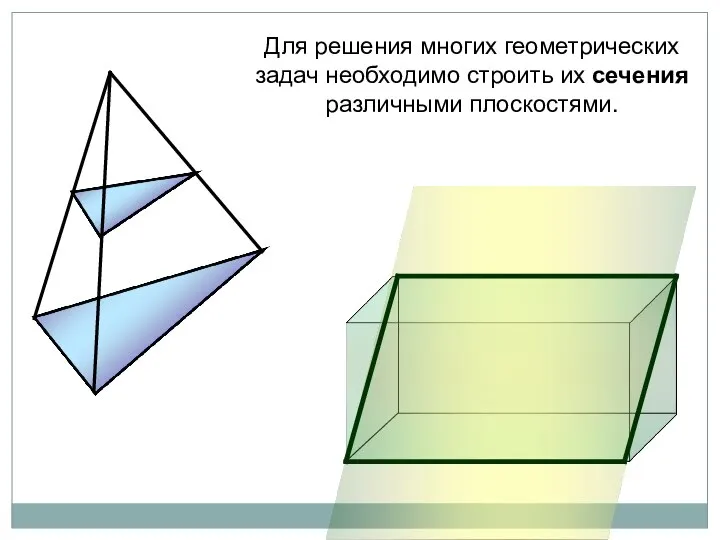
- 11. Для решения многих геометрических задач необходимо строить их сечения различными плоскостями.
- 12. 1. Соединять можно только две точки, лежащие в плоскости одной грани. Для построения сечения нужно построить
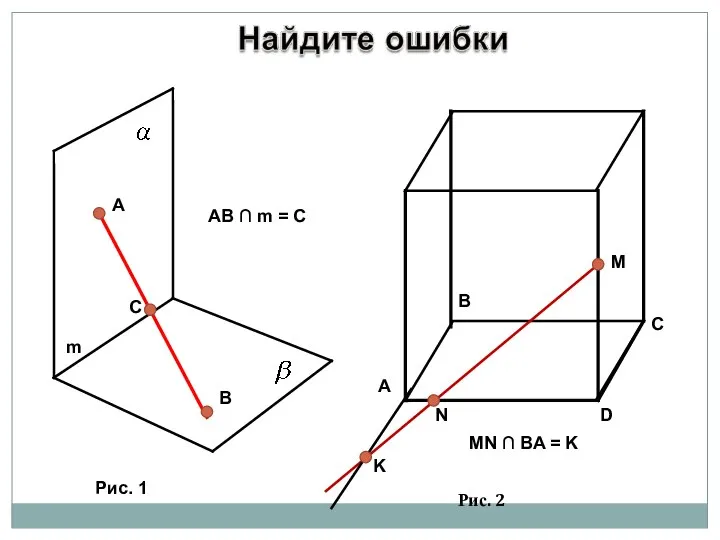
- 13. A B C m AB ∩ m = C Рис. 1 A B C D M
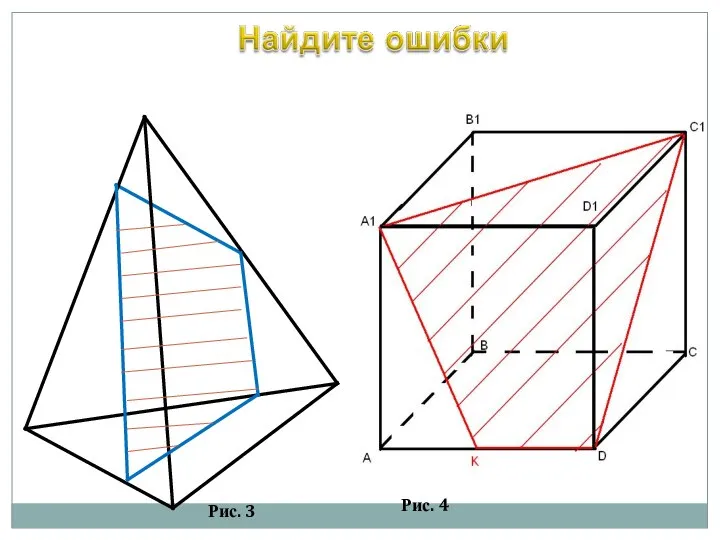
- 14. Рис. 3 Рис. 4
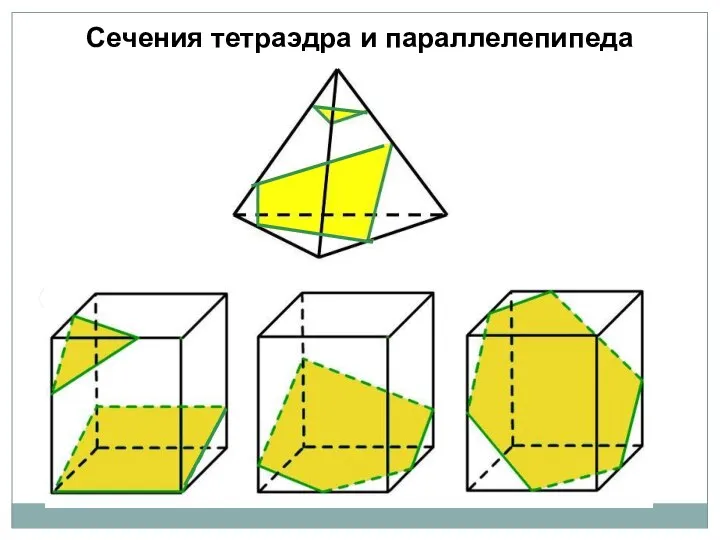
- 15. Сечения тетраэдра и параллелепипеда
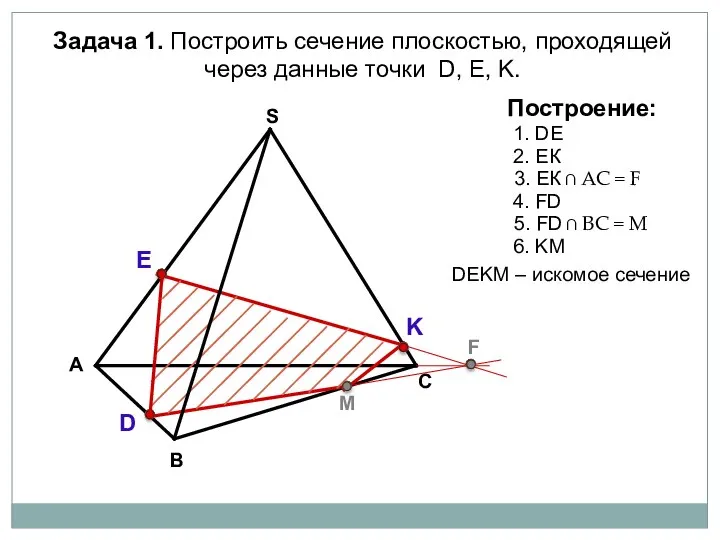
- 16. А В С S Задача 1. Построить сечение плоскостью, проходящей через данные точки D, Е, K.
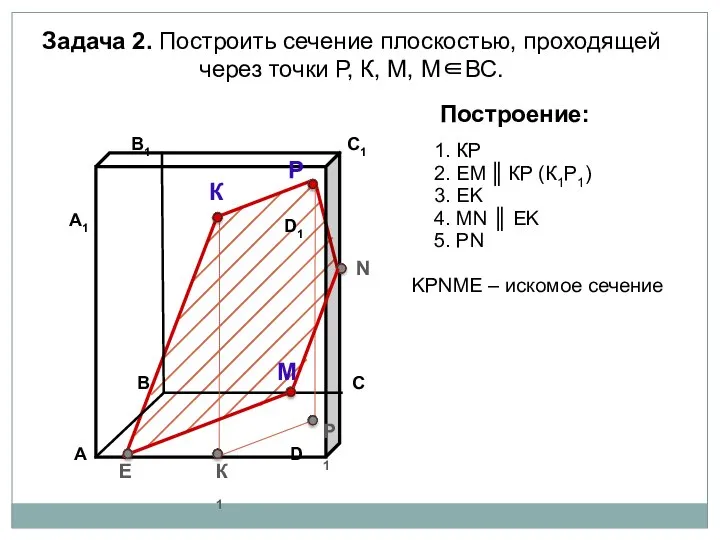
- 17. Задача 2. Построить сечение плоскостью, проходящей через точки Р, К, М, М∈ВС. К Р М Построение:
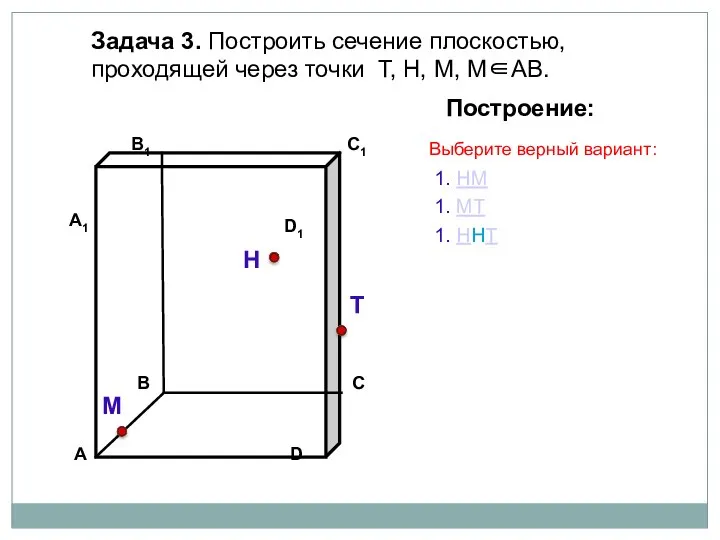
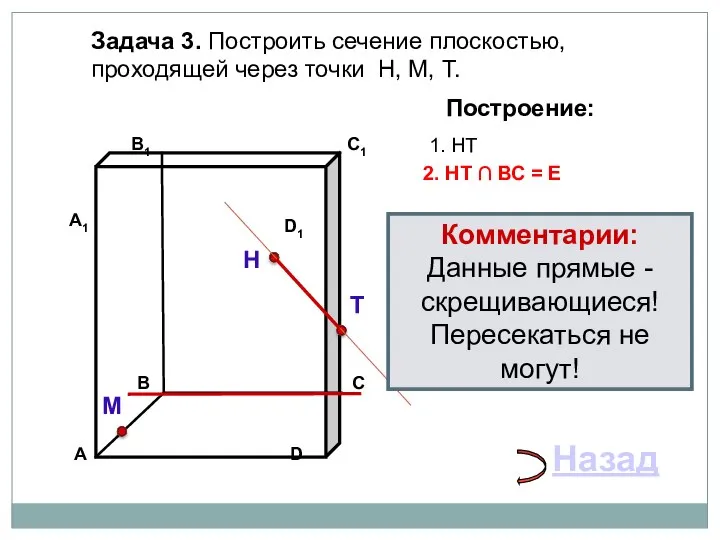
- 18. Задача 3. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М Построение:
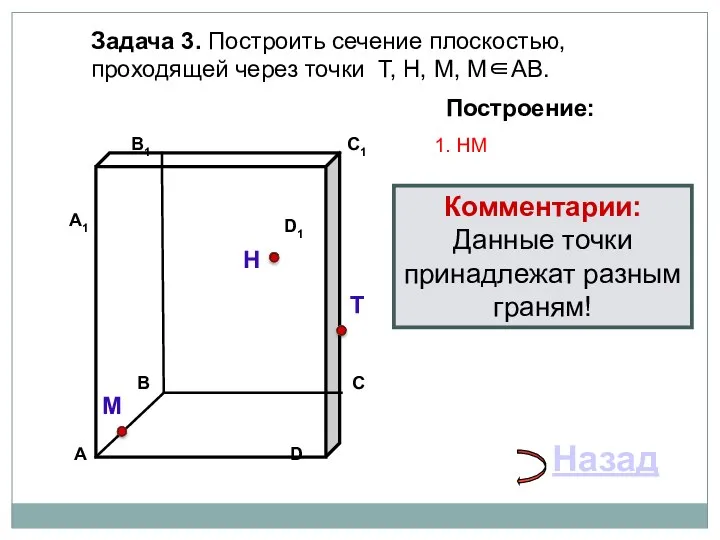
- 19. Задача 3. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М Построение:
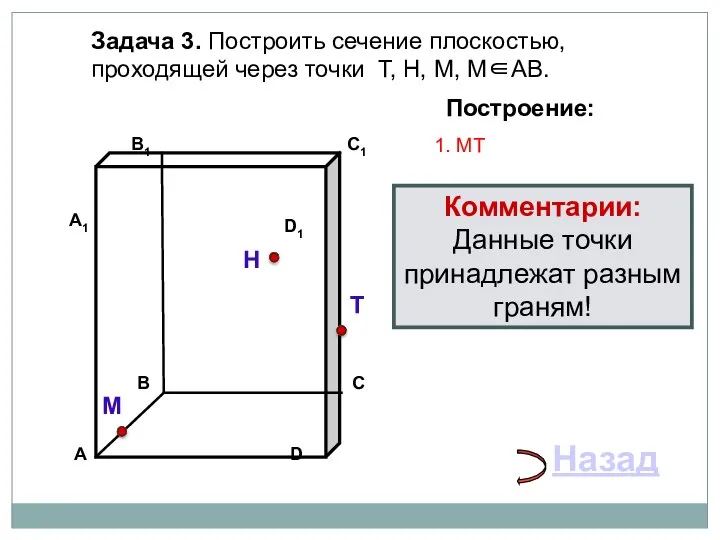
- 20. Задача 3. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М Построение:
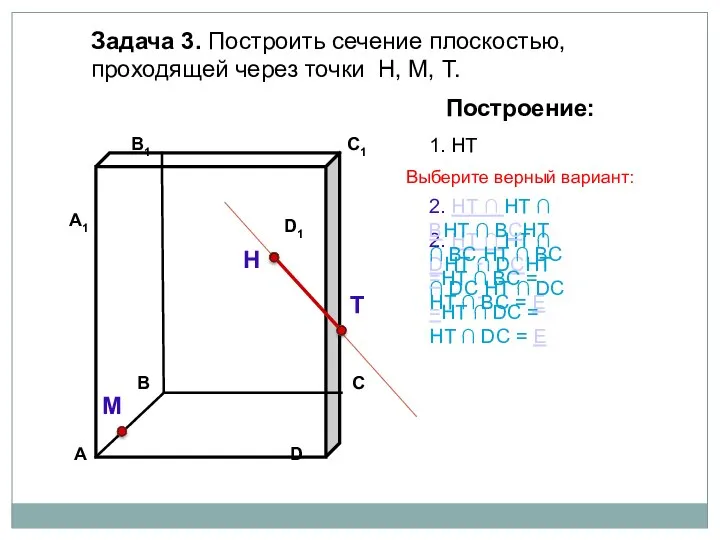
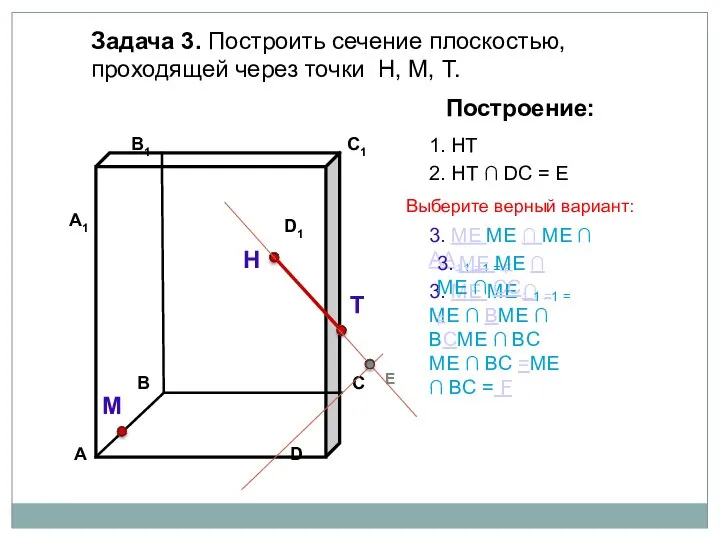
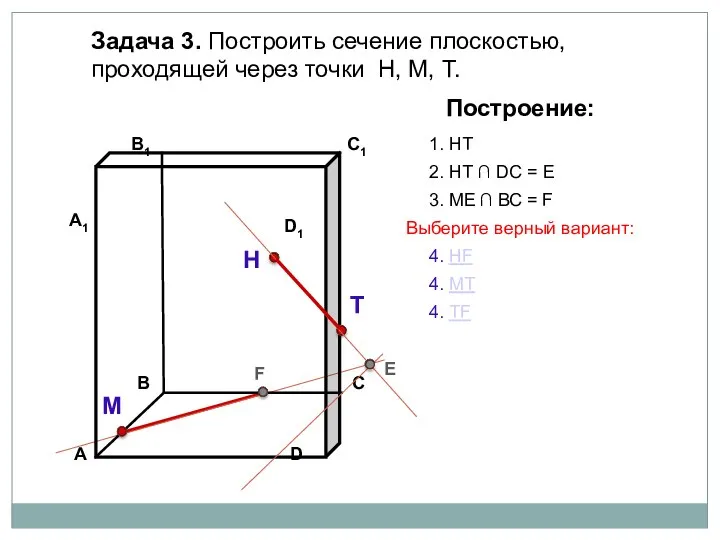
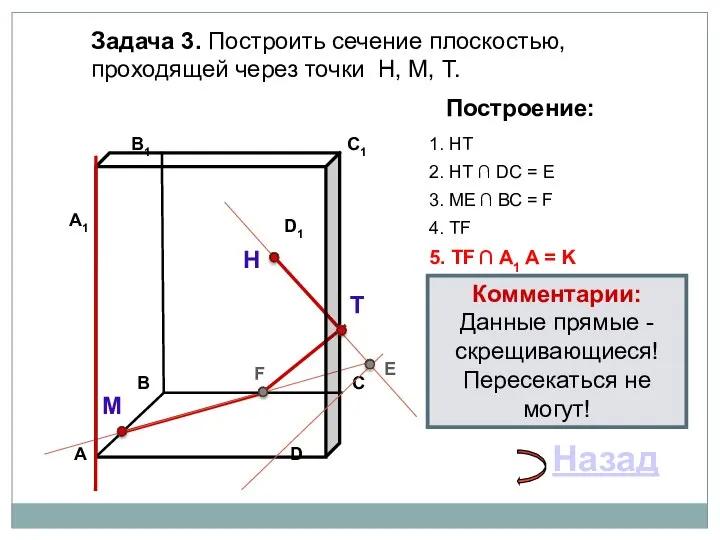
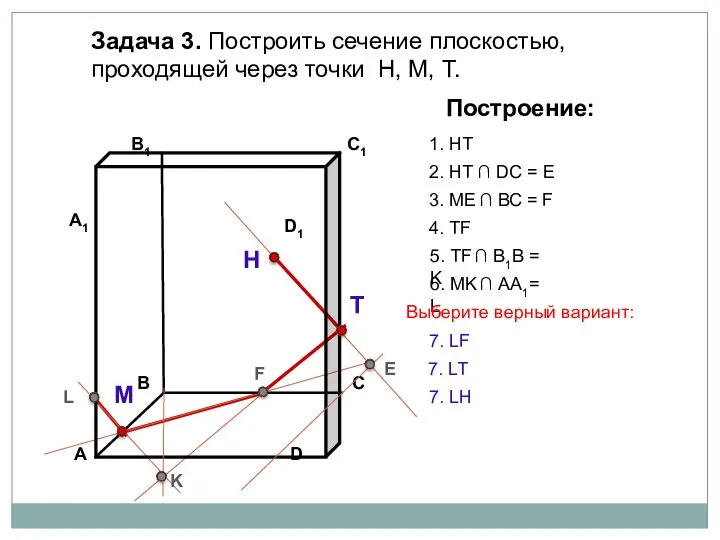
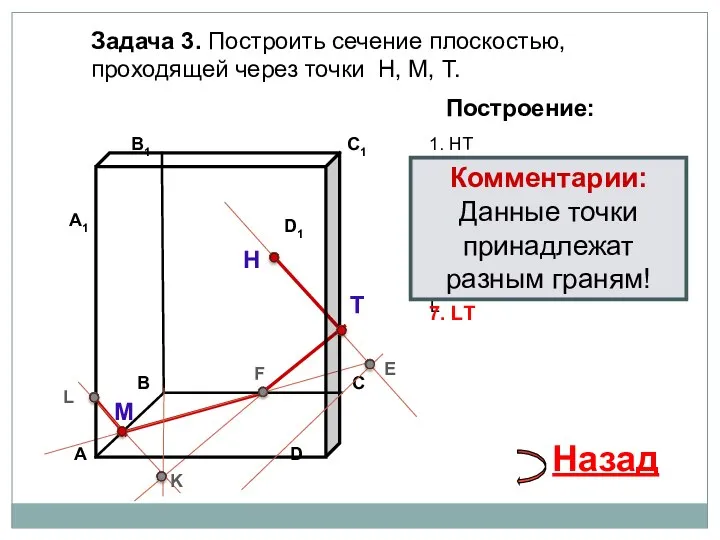
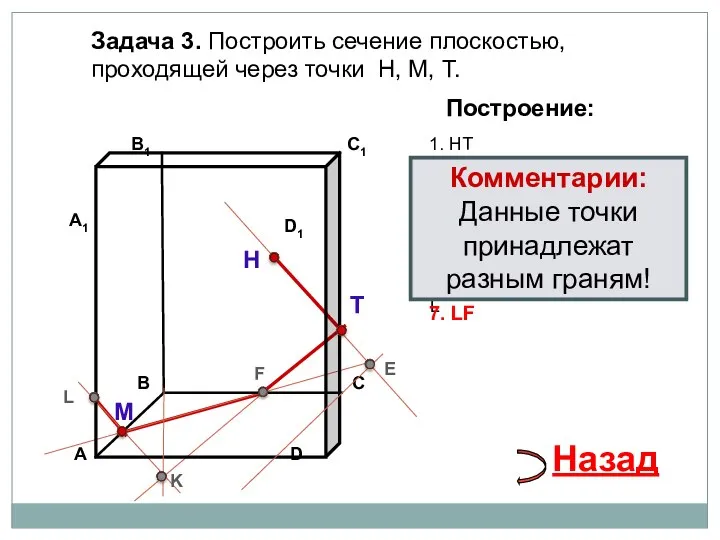
- 21. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 22. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
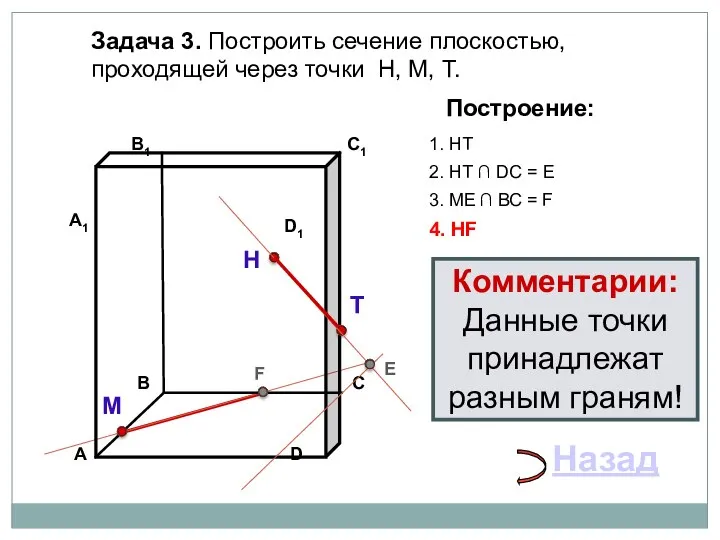
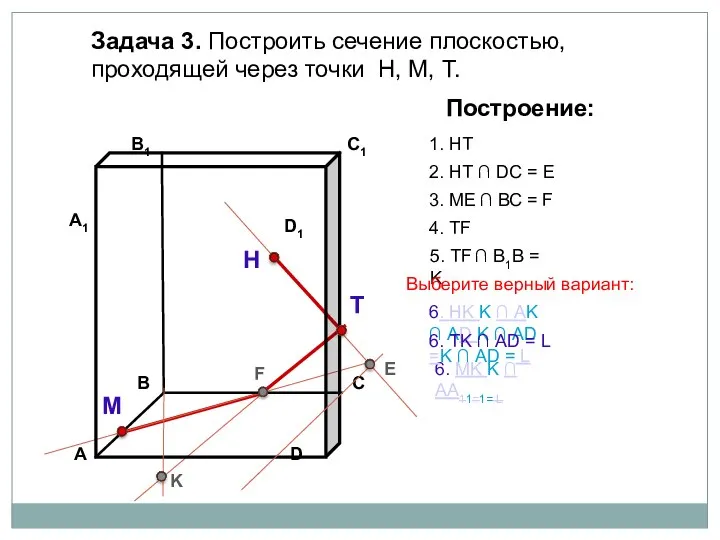
- 23. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
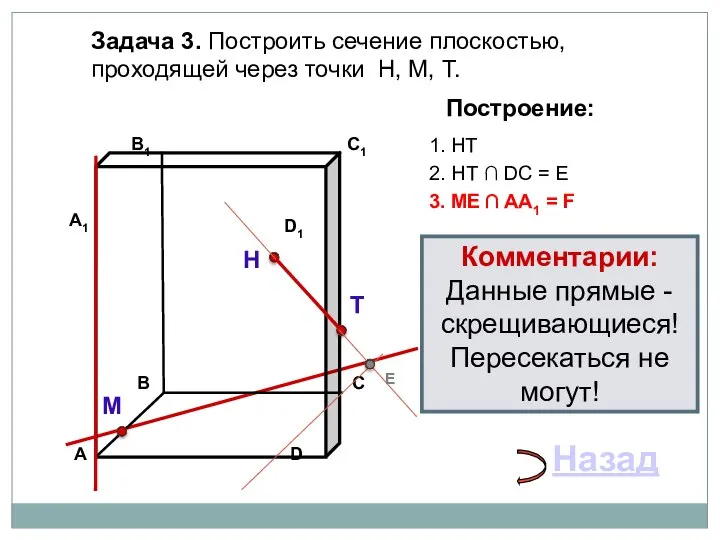
- 24. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
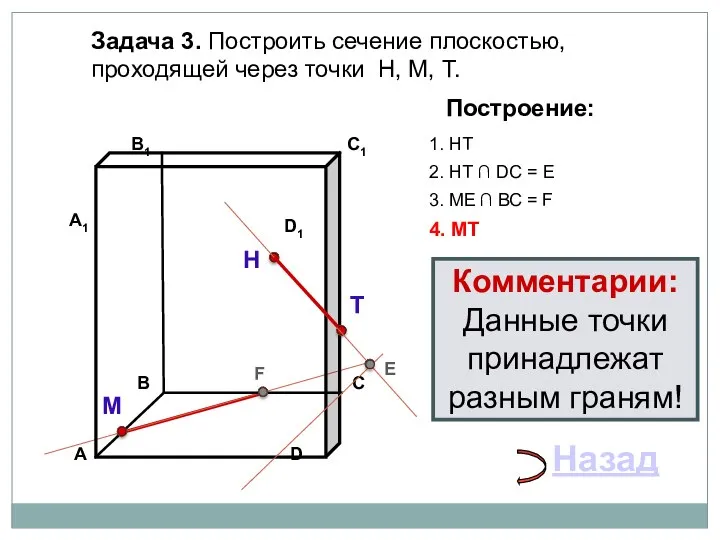
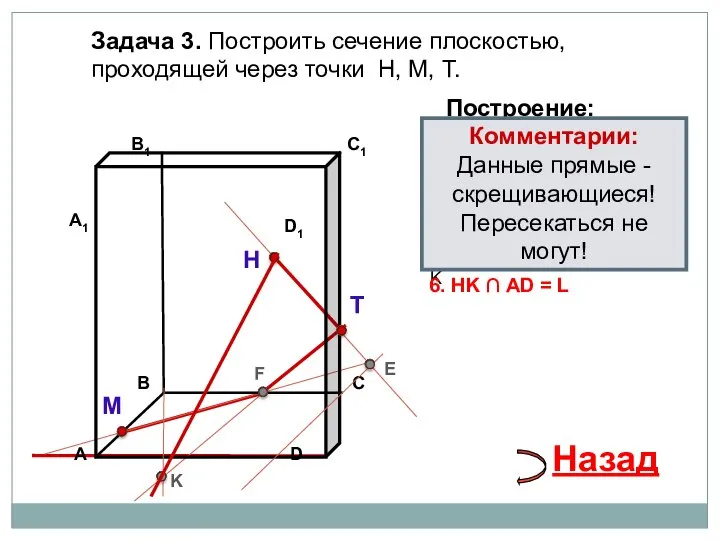
- 25. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 26. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
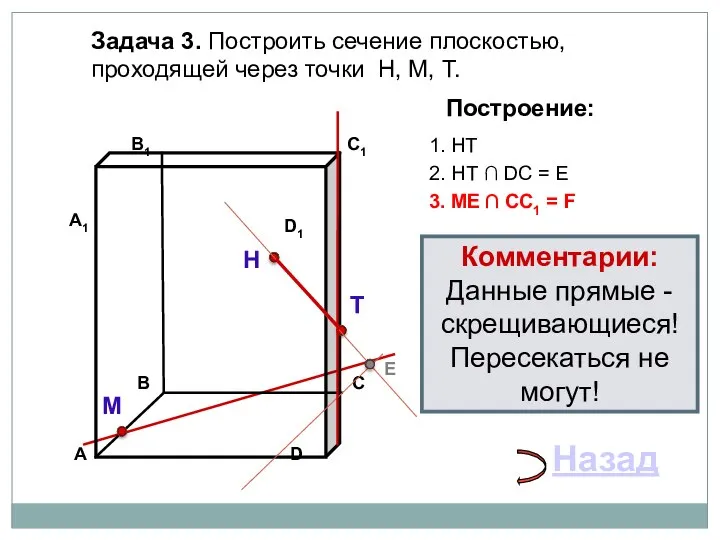
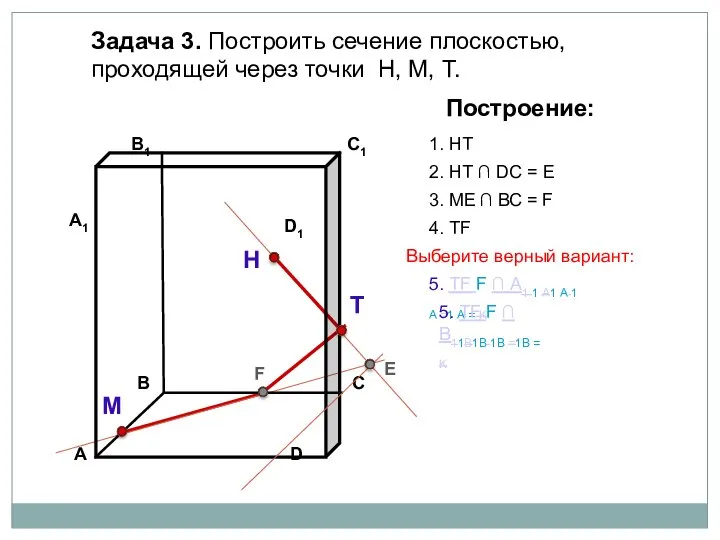
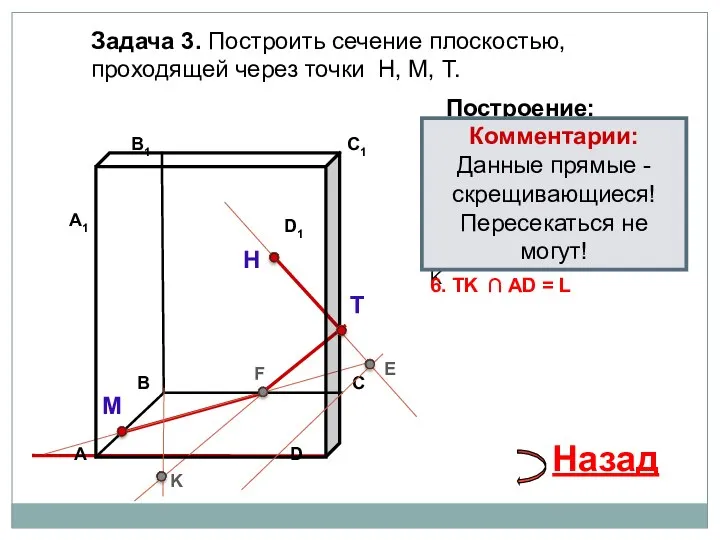
- 27. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 28. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 29. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 30. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 31. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 32. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 33. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 34. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 35. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
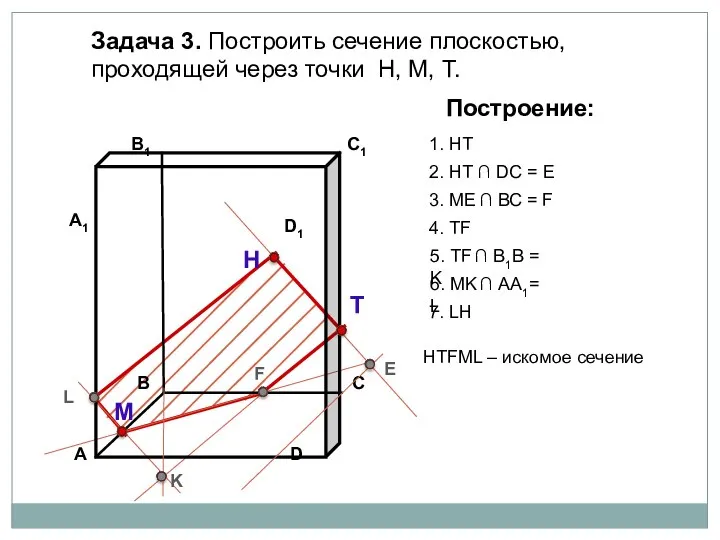
- 36. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 37. Задача 3. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
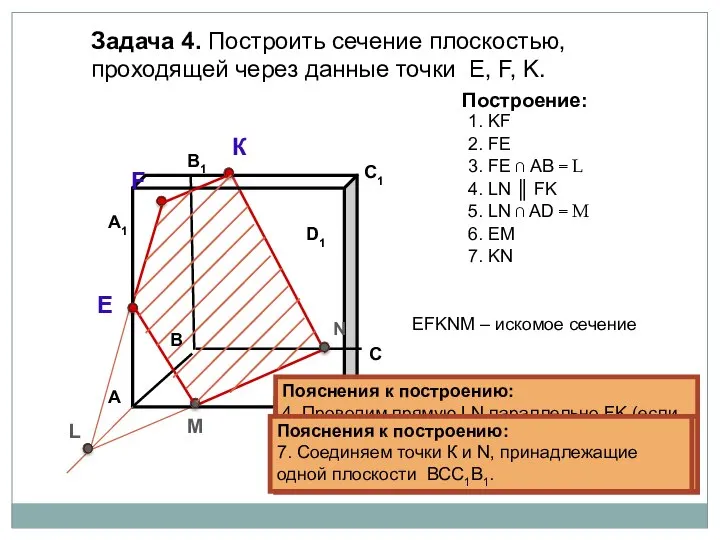
- 38. Пояснения к построению: 1. Соединяем точки K и F, принадлежащие одной плоскости А1В1С1D1. Задача 4. Построить
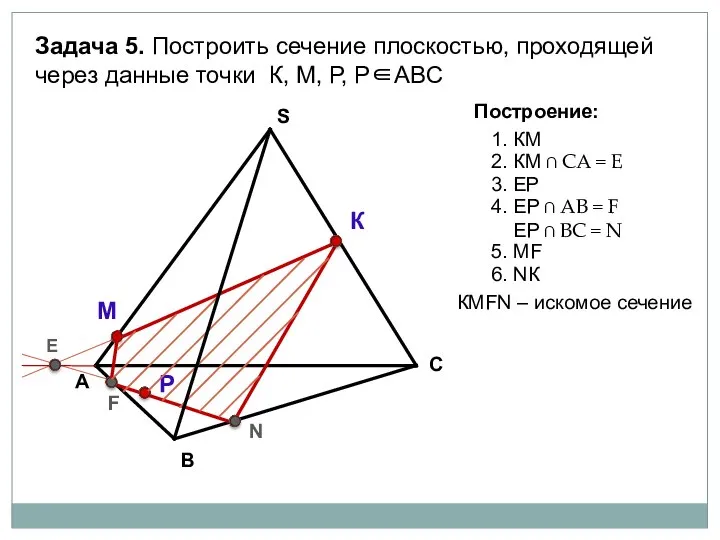
- 39. А В С S Задача 5. Построить сечение плоскостью, проходящей через данные точки К, М, Р,
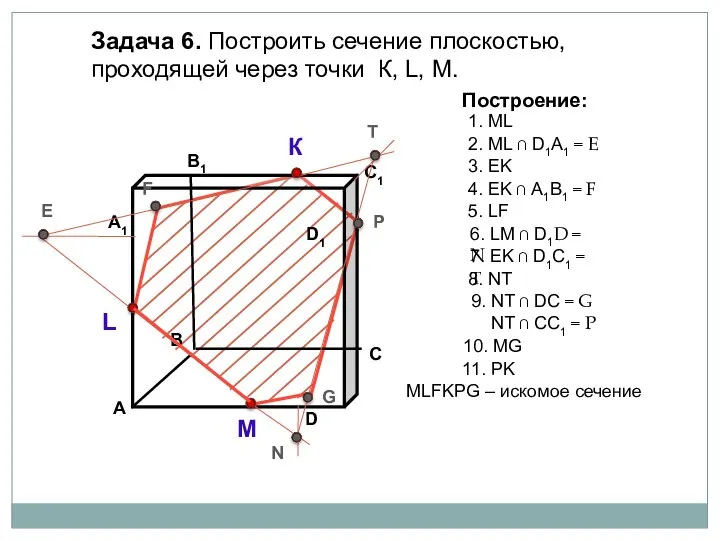
- 40. Задача 6. Построить сечение плоскостью, проходящей через точки К, L, М. К L М Построение: 1.
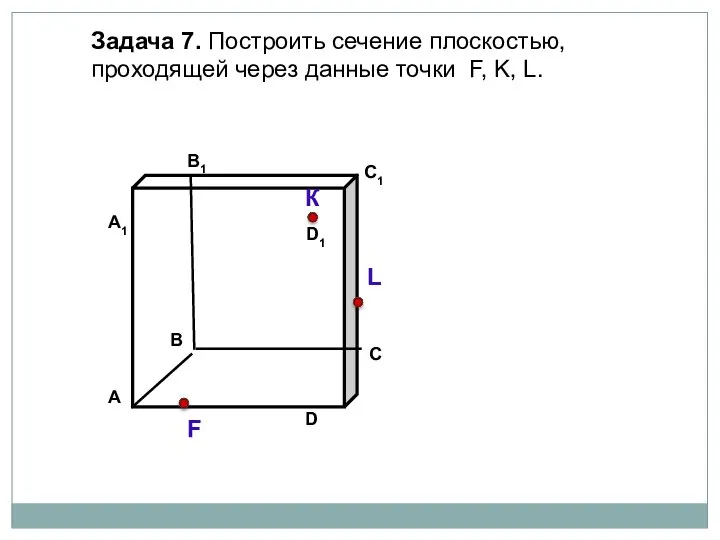
- 41. Задача 7. Построить сечение плоскостью, проходящей через данные точки F, K, L. К L F
- 43. Скачать презентацию




 Линейные операции над векторами
Линейные операции над векторами Решение задачи с использованием циклов
Решение задачи с использованием циклов Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Переместительное свойство умножения
Переместительное свойство умножения Математический тренажёр Бабушкины примеры
Математический тренажёр Бабушкины примеры Модуль комплексного числа
Модуль комплексного числа Учебный проект по алгебре Наш класс оценивает статистика
Учебный проект по алгебре Наш класс оценивает статистика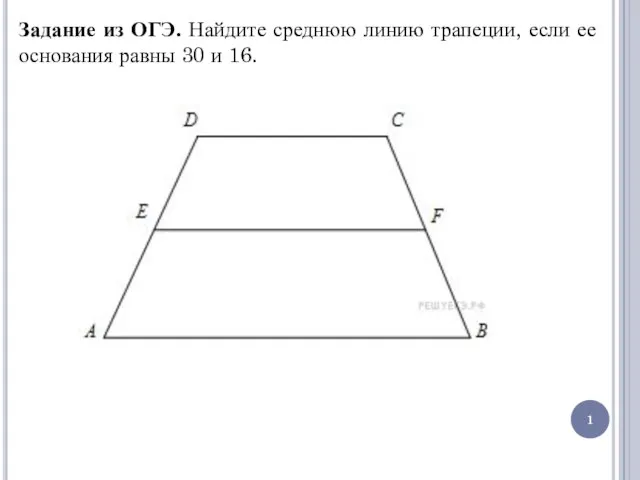 Прямоугольник. Ромб. Квадрат. Задание из ОГЭ
Прямоугольник. Ромб. Квадрат. Задание из ОГЭ Решение задач. Длина окружности. Площадь круга
Решение задач. Длина окружности. Площадь круга Заниматика. Миром управляют числа
Заниматика. Миром управляют числа СДНФ и СКНФ — два представления булевой функции
СДНФ и СКНФ — два представления булевой функции Экономические задачи
Экономические задачи Подобие треугольников и решение практических задач задач
Подобие треугольников и решение практических задач задач Презентация на тему Логарифмы с параметрами
Презентация на тему Логарифмы с параметрами  Задачи про виноград и изюм
Задачи про виноград и изюм Весёлая математика. Сколько в ширину? Сколько в высоту? Карточки для детей
Весёлая математика. Сколько в ширину? Сколько в высоту? Карточки для детей Изучение таблицы деления
Изучение таблицы деления Смешанные дроби. 5 клас
Смешанные дроби. 5 клас Действительный анализ. Глава 2. Измеримые множества
Действительный анализ. Глава 2. Измеримые множества Формула суммы п первых членов геометрической прогрессии
Формула суммы п первых членов геометрической прогрессии Иррациональные уравнения
Иррациональные уравнения Задачи на проценты
Задачи на проценты Решение примеров
Решение примеров Действительные числа. Практикум по математике. Занятие №1
Действительные числа. Практикум по математике. Занятие №1 Презентация на тему ГИА 2013. Модуль «Алгебра» №7
Презентация на тему ГИА 2013. Модуль «Алгебра» №7  Свойства арифметического корня
Свойства арифметического корня Скалярное произведение векторов. Задания
Скалярное произведение векторов. Задания Тренажер Состав числа
Тренажер Состав числа