Содержание
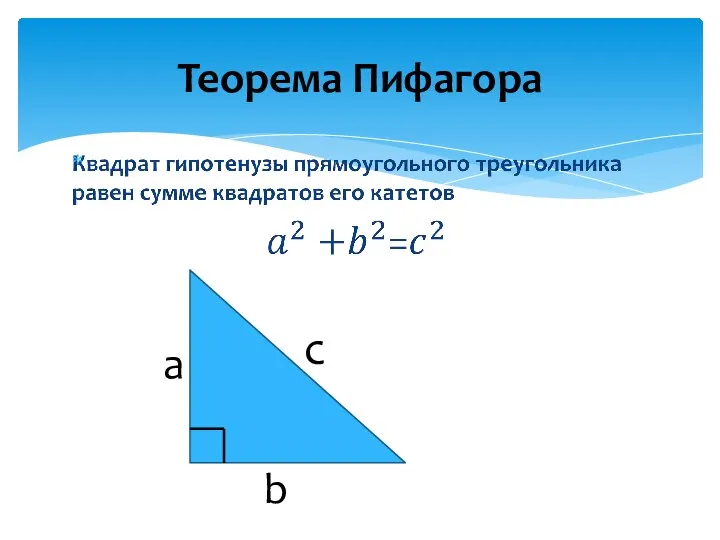
- 2. Теорема Пифагора a b c
- 3. Мориц Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5²
- 4. Ван-дер-Варден (голландский математик) сделал вывод о большой вероятности того, что теорема о квадрате гипотенузы была известна
- 5. «Принадлежит ли эта формула лично перу Пифагора…, но мы можем уверенно считать, что она принадлежит древнейшему
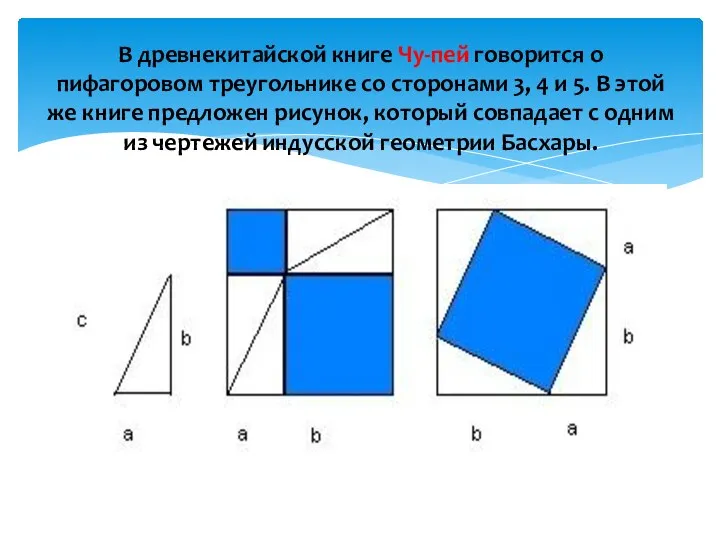
- 6. В древнекитайской книге Чу-пей говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. В этой
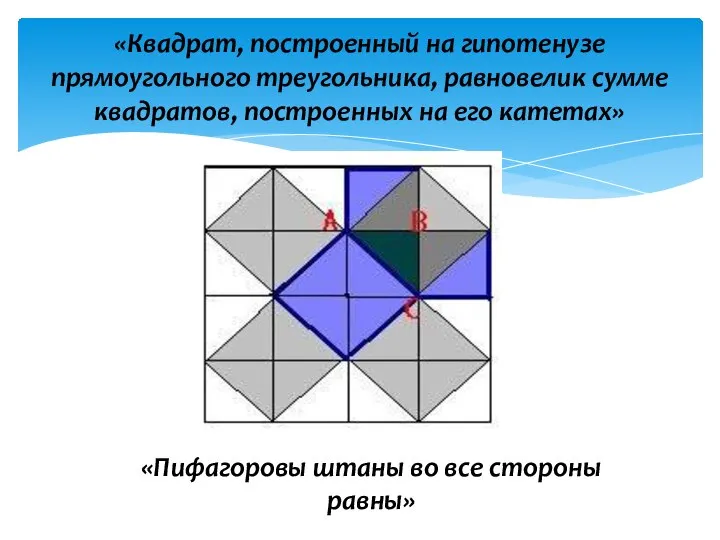
- 7. «Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах» «Пифагоровы штаны во
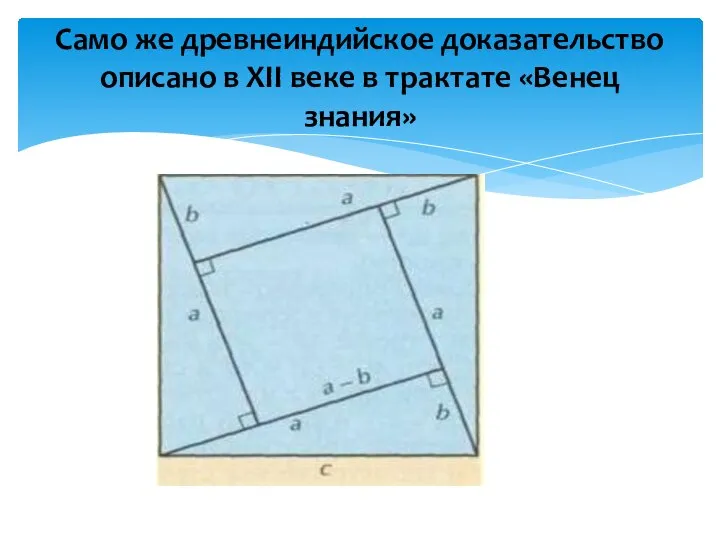
- 8. Само же древнеиндийское доказательство описано в XII веке в трактате «Венец знания»
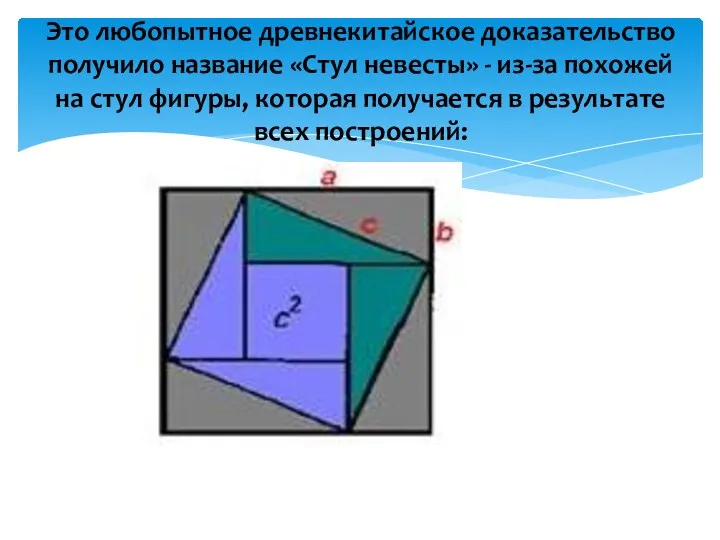
- 9. Это любопытное древнекитайское доказательство получило название «Стул невесты» - из-за похожей на стул фигуры, которая получается
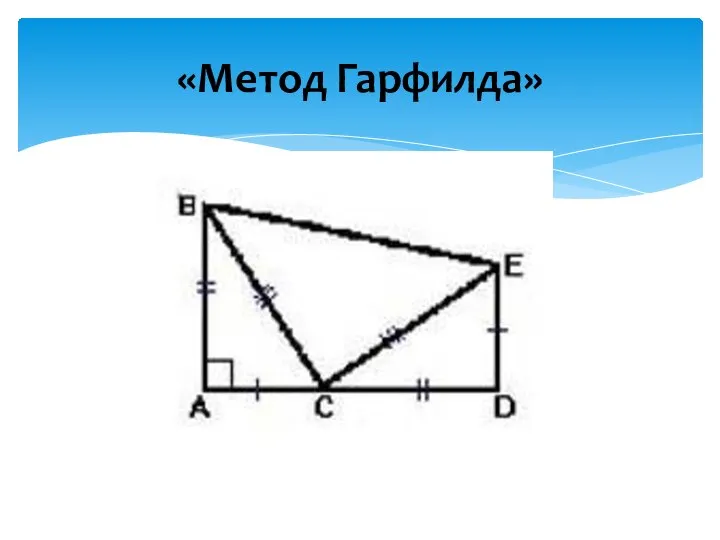
- 10. «Метод Гарфилда»
- 11. Примеры Пифагоровых троек: (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8,
- 13. Скачать презентацию




 Презентация на тему Нахождение площадей ромба, параллелограмма
Презентация на тему Нахождение площадей ромба, параллелограмма  Как математика учит критическому мышлению
Как математика учит критическому мышлению Граф – набор точек, некоторые из которых соединены линиями
Граф – набор точек, некоторые из которых соединены линиями Параллельные прямые
Параллельные прямые Умножение двузначных чисел
Умножение двузначных чисел Десятичные дроби по-английски. Бинарный урок
Десятичные дроби по-английски. Бинарный урок Симметрия относительно точки
Симметрия относительно точки Удивительный мир математики
Удивительный мир математики Преобразование графиков функций
Преобразование графиков функций Производная в ЕГЭ
Производная в ЕГЭ Законы булевой алгебры
Законы булевой алгебры Показательные неравенства и уравнения
Показательные неравенства и уравнения Производная произведения двух функций
Производная произведения двух функций Цилиндр. Сечения цилиндра
Цилиндр. Сечения цилиндра Презентация на тему Формирование УУД на уроках математики в 5 классе
Презентация на тему Формирование УУД на уроках математики в 5 классе  Вычисление углов между прямыми и плоскостями
Вычисление углов между прямыми и плоскостями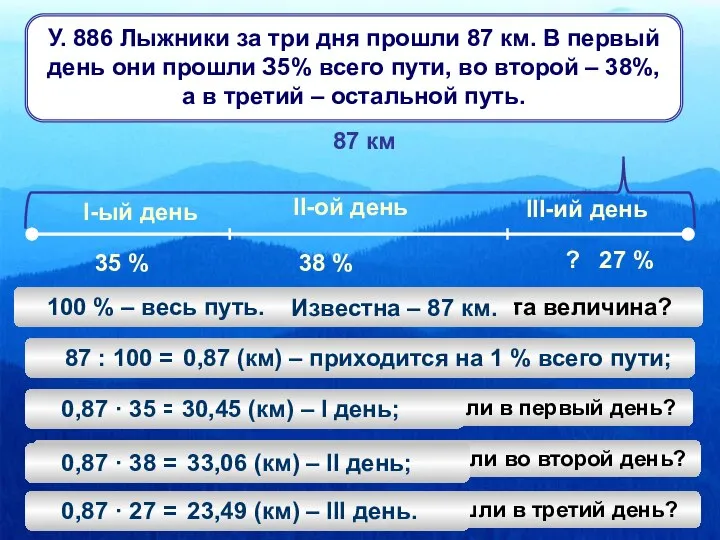 Задачи о лыжниках
Задачи о лыжниках Приём деления для случаев вида: 87: 29, 66 : 22
Приём деления для случаев вида: 87: 29, 66 : 22 Пифагория. Геометрия в клетках. Геймификация обучения
Пифагория. Геометрия в клетках. Геймификация обучения Признаки равенства треугольников
Признаки равенства треугольников Иррациональные неравенства и способы их решения
Иррациональные неравенства и способы их решения Шкала. Координатный луч
Шкала. Координатный луч Формы работы при подготовке к ЕГЭ
Формы работы при подготовке к ЕГЭ Комбинаторика
Комбинаторика Презентация на тему Шутка гениев: флексагон
Презентация на тему Шутка гениев: флексагон  Измерение и построение углов
Измерение и построение углов Решение уравнений. Тест
Решение уравнений. Тест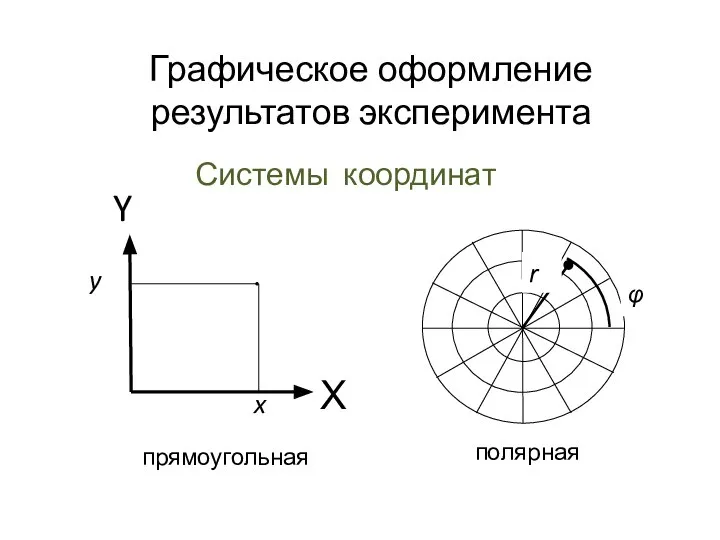 Графическое оформление результатов эксперимента
Графическое оформление результатов эксперимента