Содержание
- 2. Любой многочлен P(x), содержащий только переменное х и его натуральные степени, можно записать в стандартном виде
- 3. В результате сложения, вычитания и умножения многочленов получаются многочлены. Особое место в теории многочленов занимает деление
- 4. Разделить уголком многочлен P(x) = 10x2 − 7х− 12 на Q(x) = 5х +4 10x2 −
- 5. Пример 1 : Разделить многочлен P(x) = 3x4 + 2x2 – 1 на многочлен Q(x) =
- 6. P(x) = M(x)⋅ Q(x) + R(x) где M(x) – частное, степень которого m = n –
- 7. − Чтобы разделить многочлен P(x) на многочлен Q(x) нужно: Расположить делимое и делитель по убывающим степеням
- 8. Пример 2 : Разделить многочлен 3х + 4x4 + 1 – 15х3 + 2х5 – 9x2
- 9. Свойства делимости многочленов 1. Если многочлен P(x) делится на многочлен Q(x), а многочлен Q(x) делится на
- 10. Найдите частное: (x2 +3х − 4):(х + 4) (x2 − 7х + 10):(х − 5) (6x3
- 12. Скачать презентацию









 Элективный курс по теории вероятностей
Элективный курс по теории вероятностей Многочлен и его стандартный вид
Многочлен и его стандартный вид Музей по истории геометрии
Музей по истории геометрии Преобразование графиков функций. Памятка для учащихся
Преобразование графиков функций. Памятка для учащихся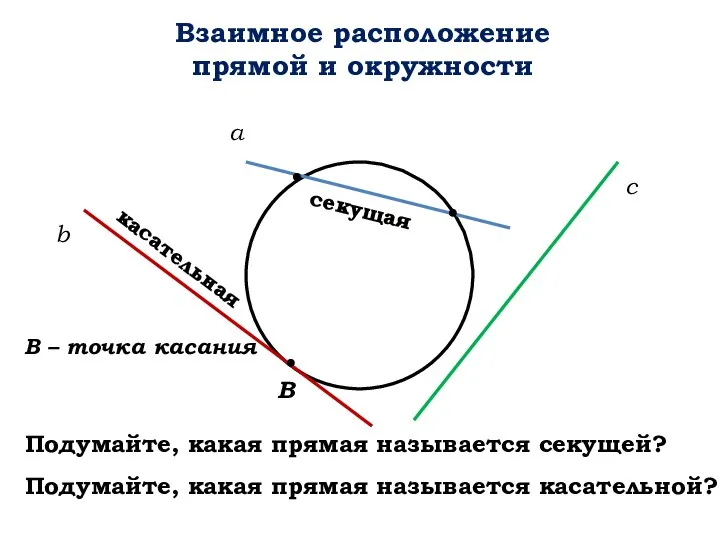 Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Логарифмические неравенства
Логарифмические неравенства Турнир имени Лоповка
Турнир имени Лоповка Старинные меры массы и длины
Старинные меры массы и длины Проценты (1)
Проценты (1) Официальная статистика как условие устойчивого развития сельского хозяйства
Официальная статистика как условие устойчивого развития сельского хозяйства Задачи на нахождение экстремума
Задачи на нахождение экстремума Система уравнений. Метод алгебраического сложения
Система уравнений. Метод алгебраического сложения Сумма углов треугольника. 7 класс
Сумма углов треугольника. 7 класс Математический биатлон
Математический биатлон Окружность и прямая
Окружность и прямая Пересечение высот
Пересечение высот Проценты в нашей жизни. Решение задач
Проценты в нашей жизни. Решение задач Решение уравнений. Буквенные выражения
Решение уравнений. Буквенные выражения Разложение вектора по базису
Разложение вектора по базису Числовые последовательности
Числовые последовательности Интерполяционный многочлен Лагранжа
Интерполяционный многочлен Лагранжа Объемы прямой призмы и цилиндра (11 класс)
Объемы прямой призмы и цилиндра (11 класс) Домашняя математика
Домашняя математика Решение задач по теме Треугольники. 7 класс
Решение задач по теме Треугольники. 7 класс Презентация на тему Функция. График функции.
Презентация на тему Функция. График функции.  Презентация на тему Сумма и разность десятичных дробей
Презентация на тему Сумма и разность десятичных дробей  Поиск преступника. Решение логической задачи
Поиск преступника. Решение логической задачи Подготовка к ЕГЭ. Решение задач на движение
Подготовка к ЕГЭ. Решение задач на движение