Слайд 2Динамическая система
(1)
Уравнение
может быть использовано для описания динамики популяции с неперекрывающимися поколениями.

Функция F(N) обладает следующими свойствами:
F(N) > 0 ∀ допустимого N > 0;
F(0) = 0;
F(N) возрастает в окрестности точки N = 0;
F(N) → k = const ≥ 0 при N → +∞.
Определение 1. Решением уравнения (1) называется числовая последовательность {Nt}t=0,1,2,…., члены которой удовлетворяют уравнению (1).
Слайд 3Основные определения
Определение 2. Решение уравнения (1) вида Nt = N* = const

∀ t = 0,1,2, … называется стационарным, а точка N* − положением равновесия (или точкой покоя, стационарной точкой).
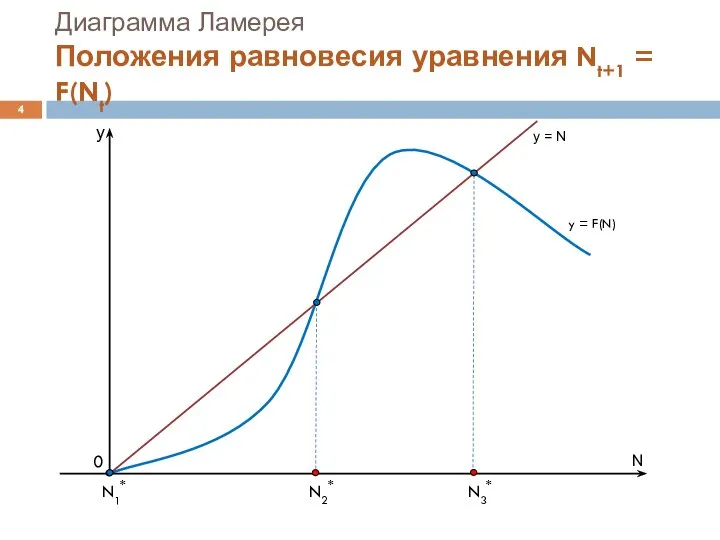
Все положения равновесия являются корнями уравнения:
F(N) = N (2)
Определение 3. Стационарное решение Nt = N* ∀ t = 0,1,2, … называется устойчивым, если ∀ ε > 0 ∃ δ > 0, такое, что |Nt − N*| < ε ∀t ≥ 0, если |N0 − N*| < δ.
Определение 4. Если когда |N0 − N*| < δ, то решение Nt = N* ∀ t = 0,1,2, … называется асимптотически устойчивым.
Слайд 4Диаграмма Ламерея
Положения равновесия уравнения Nt+1 = F(Nt)
N
y
y = F(N)
y =
Слайд 5N0
Диаграмма Ламерея (лестница Ламерея)
Решение уравнения Nt+1 = F(Nt)
y = N
y
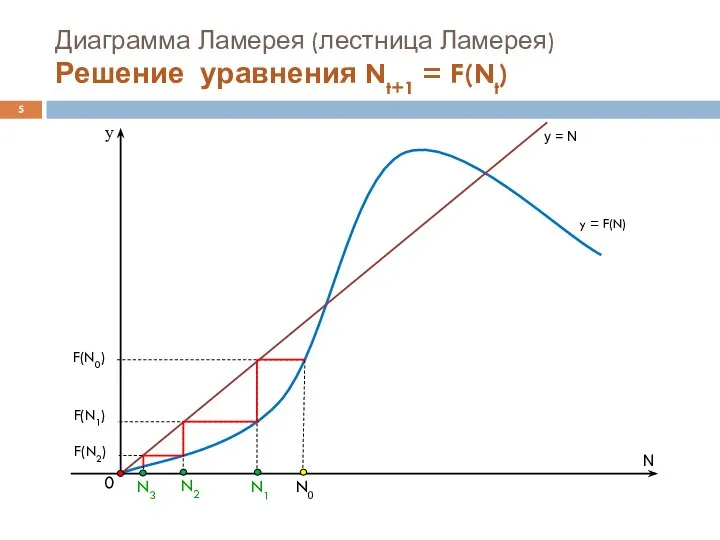
= F(N)
N
y
F(N0)
N2
N1
0
F(N1)
F(N2)
N3
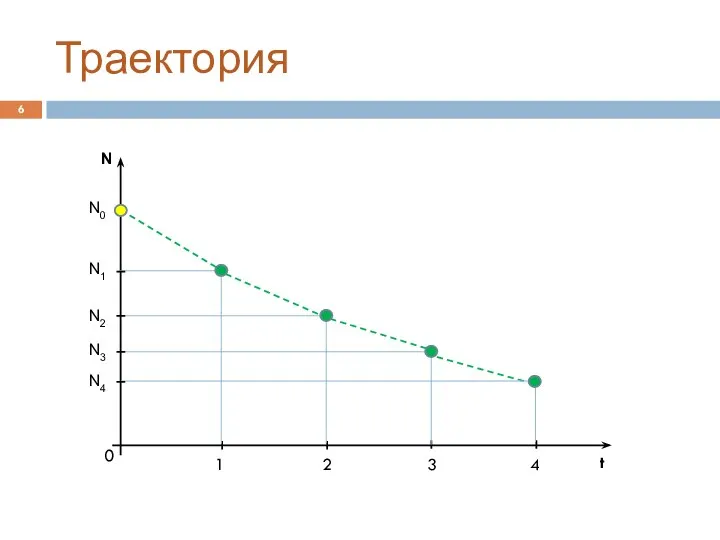
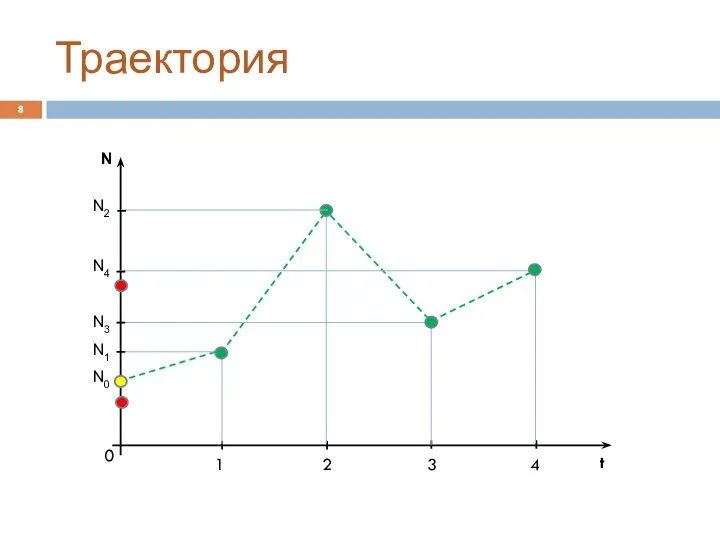
Слайд 6Траектория
N
t
0
1
2
3
4
N0
N2
N3
N4
N1
Слайд 7N0
Диаграмма Ламерея (лестница Ламерея)
Решение уравнения Nt+1 = F(Nt)
y = N
y
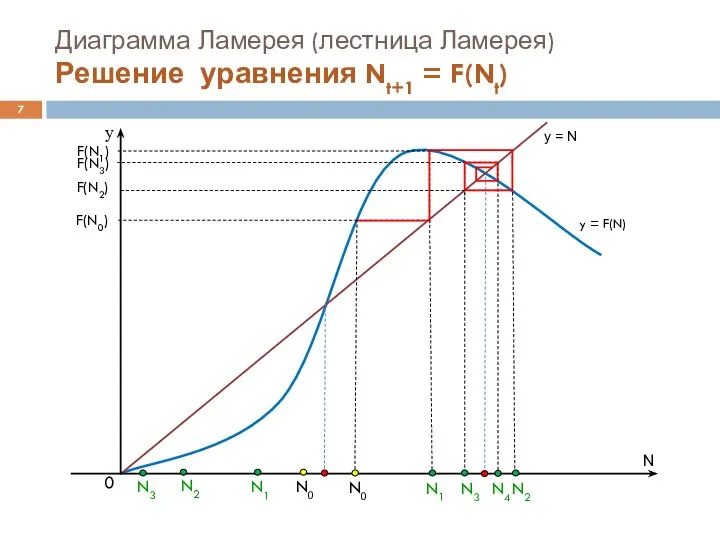
= F(N)
N
y
F(N1)
N2
N1
0
F(N0)
F(N2)
N3
N0
N1
N2
N3
F(N3)
N4
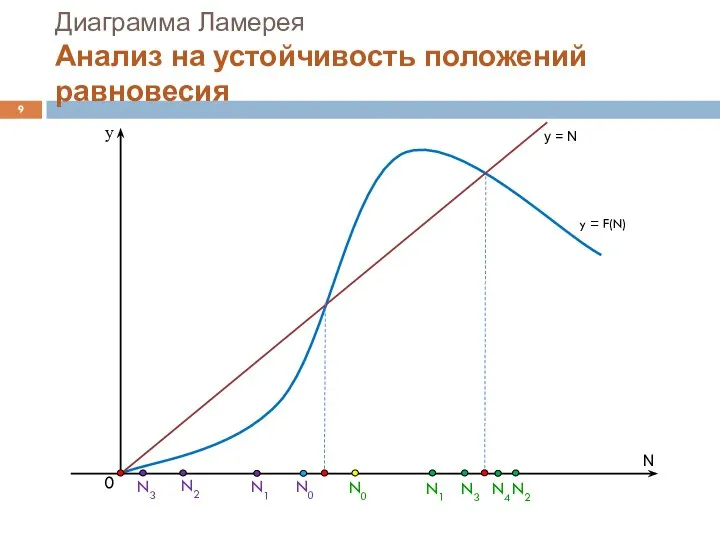
Слайд 9N0
Диаграмма Ламерея
Анализ на устойчивость положений равновесия
y = N
y = F(N)
N
y
N2
N1
0
N3
N0
N1
N2
N3
N4







 Сложение векторов
Сложение векторов Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс Презентация на тему Решение уравнений графическим способом
Презентация на тему Решение уравнений графическим способом  Начальные понятия геометрии
Начальные понятия геометрии Алгебра. Число. Уравнение. Тождество. Функция
Алгебра. Число. Уравнение. Тождество. Функция Неравенства и их системы
Неравенства и их системы Решение тригонометрических уравнений
Решение тригонометрических уравнений Многоугольники (n-угольники)
Многоугольники (n-угольники) Интегрированный урок: Многогранники вокруг нас
Интегрированный урок: Многогранники вокруг нас Формулы площади
Формулы площади Презентация на тему Описательная статистика
Презентация на тему Описательная статистика  Робот Гоша ведёт занятие по ФЭМП
Робот Гоша ведёт занятие по ФЭМП Системы случайных величин
Системы случайных величин Векторы в пространстве. Понятие вектора
Векторы в пространстве. Понятие вектора Презентация на тему Метод координат в пространстве
Презентация на тему Метод координат в пространстве  Задания по математике (5 класс, часть 6)
Задания по математике (5 класс, часть 6) Производная функции. Тест 1
Производная функции. Тест 1 Равенство геометрических фигур
Равенство геометрических фигур Theorem of rational root with integral coefficients
Theorem of rational root with integral coefficients Презентация на тему Задачи на увеличение и уменьшение числа (1 класс)
Презентация на тему Задачи на увеличение и уменьшение числа (1 класс)  Состав числа 10
Состав числа 10 Симметрия в пространстве
Симметрия в пространстве Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях
Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях Математика и физика здоровья
Математика и физика здоровья Школа олимпийского резерва. (задача)
Школа олимпийского резерва. (задача) Презентация на тему ЛОГАРИФМ ЧИСЛА
Презентация на тему ЛОГАРИФМ ЧИСЛА  Синтез автоматов без памяти
Синтез автоматов без памяти Формирование элементарных математических представлений
Формирование элементарных математических представлений