Вычисление объемов тел вращения

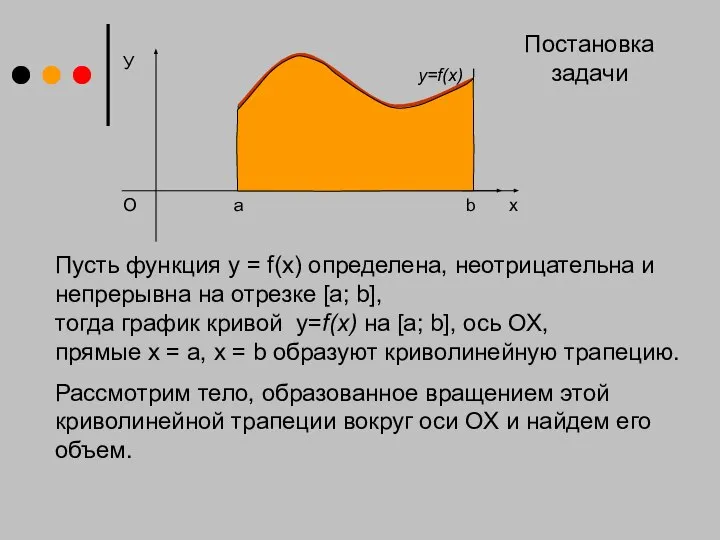
У
х
y=f(x)
O
Пусть функция y = f(x) определена, неотрицательна и непрерывна на отрезке [a; b],
тогда график кривой у=f(x) на [a; b], ось OX,
прямые x = a, x = b образуют криволинейную трапецию.
Рассмотрим тело, образованное вращением этой криволинейной трапеции вокруг оси OX и найдем его объем.
a
b
Постановка задачи

У
х
y=f(x)
O
Разобьем отрезок [a;b] на n частей произвольным образом, через каждую точку деления проведем плоскость, перпендикулярную к оси ОХ и найдём площади полученных поперечных сечений.
Очевидно, что любое поперечное сечение тела вращения – круг. Радиус круга равен значению функции в хс
Площадь этого круга – S(x) = π· f 2 (xс)

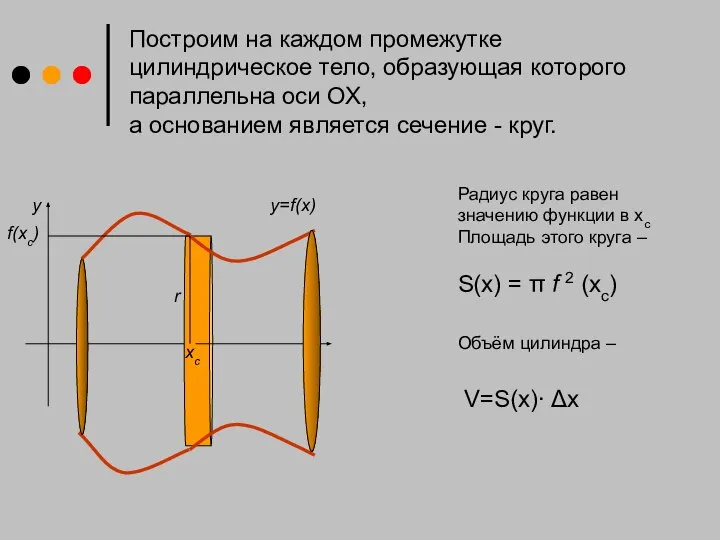
Построим на каждом промежутке цилиндрическое тело, образующая которого параллельна оси ОХ,
а основанием является сечение - круг.
Радиус круга равен
значению функции в хс
Площадь этого круга –
S(x) = π f 2 (xс)
Объём цилиндра –
V=S(x)∙ Δx
y=f(x)
f(xс)
y
xс
r

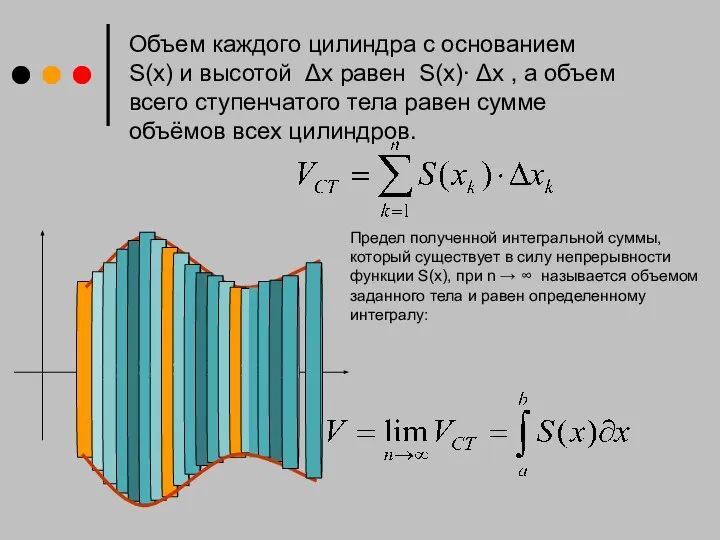
Объем каждого цилиндра с основанием S(x) и высотой Δx равен S(x)∙ Δx , а объем всего ступенчатого тела равен сумме объёмов всех цилиндров.
Предел полученной интегральной суммы, который существует в силу непрерывности функции S(x), при n → ∞ называется объемом заданного тела и равен определенному интегралу:

Тогда объем тела вращения вокруг оси ОХ:
Если тело образовано вращением криволинейной трапеции, образованной функцией у=f(x) на отрезке [a;b],вокруг оси ОХ, то его объём можно найти по формуле:
Предел полученной интегральной суммы, при n → ∞ равен определенному интегралу:
x
y=f(x)
y

Задача.
Пусть тело образовано вращением параболы у=х2 на отрезке [0;2] вокруг оси ОХ.
Найдите объём тела вращения.
у=х2
у
О
х
2

Задача.
Пусть тело образовано вращением функции у=0,5x на отрезке [0;4] вокруг оси ОХ.
Найдите объём тела вращения.
y
O
x
4

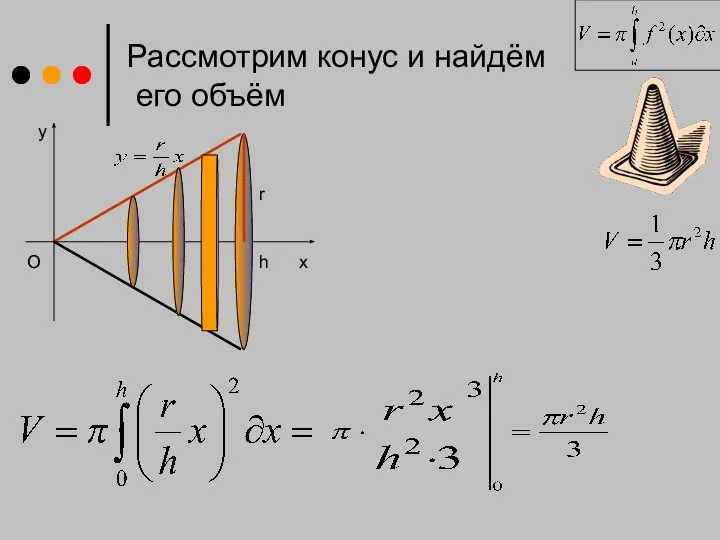
x
Рассмотрим конус и найдём
его объём
y
h
O
r

x
Рассмотрим усечённый конус и найдём его объём
y
h
O
R
r

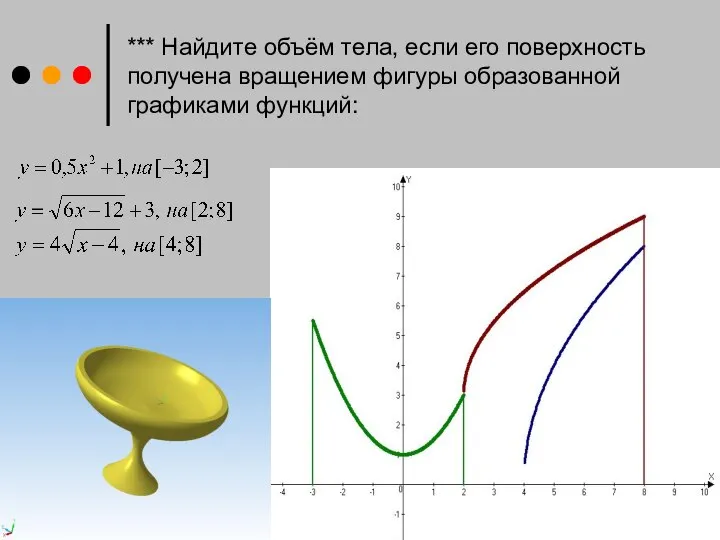
*** Найдите объём тела, если его поверхность получена вращением фигуры образованной графиками функций:

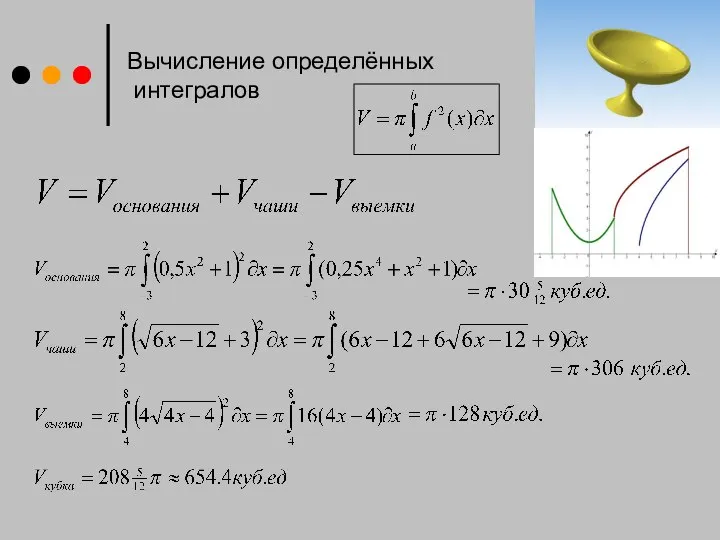
Вычисление определённых
интегралов

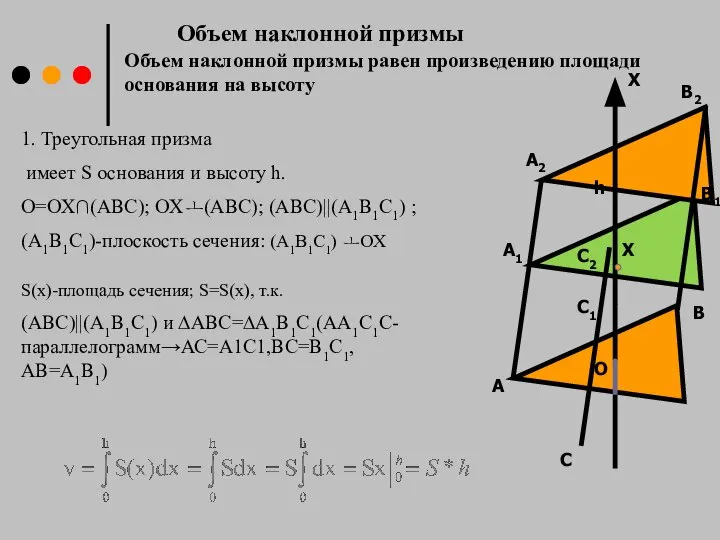
A
A1
A2
B
B1
B2
C
C1
C2
O
X
h
X
Объем наклонной призмы
Объем наклонной призмы равен произведению площади основания на высоту
1. Треугольная призма
имеет S основания и высоту h.
O=OX∩(АВС); OXᅩ(АВС); (АВС)||(А1В1С1) ;
(А1В1С1)-плоскость сечения: (А1В1С1) ᅩOX
S(x)-площадь сечения; S=S(x), т.к.
(АВС)||(А1В1С1) и ∆ABC=∆A1B1C1(АА1С1С-параллелограмм→АС=А1С1,ВС=В1С1, АВ=А1В1)

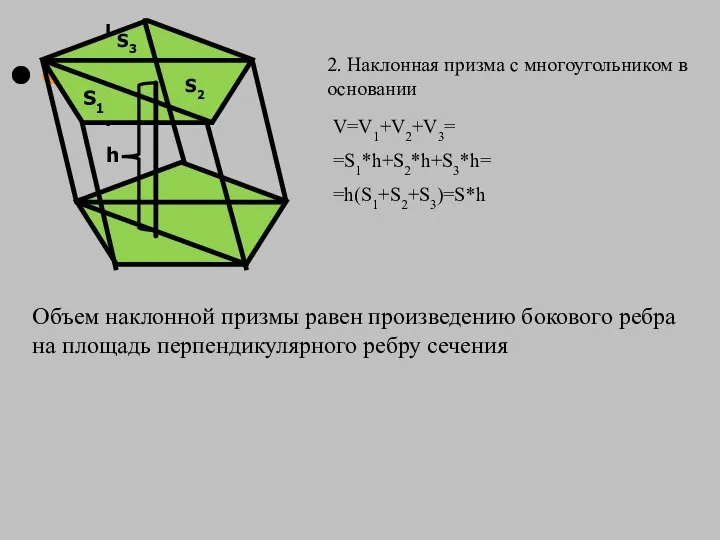
V=V1+V2+V3=
=S1*h+S2*h+S3*h=
=h(S1+S2+S3)=S*h
S1
S2
S3
h
Объем наклонной призмы равен произведению бокового ребра на площадь перпендикулярного ребру сечения
2. Наклонная призма с многоугольником в основании

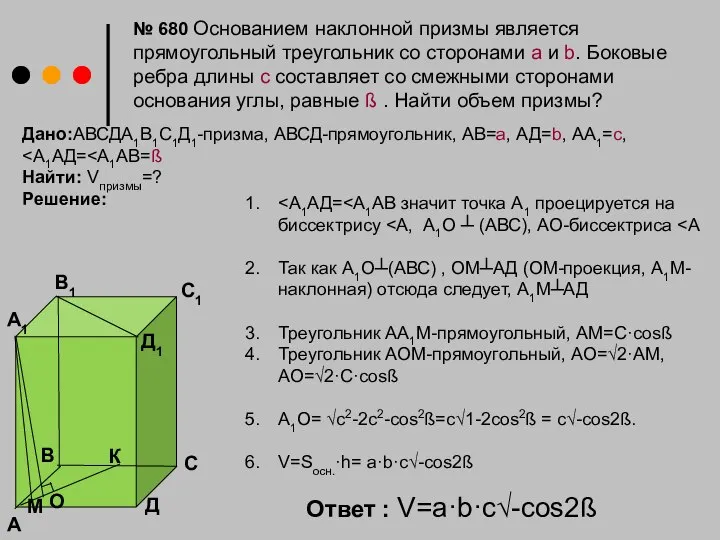
№ 676 Найти объем наклонной призмы, у которой основанием является треугольник со сторонами 10см,10см,12см, а боковое ребро равное 8см, составляет с плоскостью основания угол 600
V= SАВС* h , Sосн.=√р(р-а)(р-b)(р-с) - формула Герона
Sосн.=√16*6*4*6 = 4*2*6 = 48 (см2)
Ответ: Vпр. = 192√3 (см3)
Треугольник ВВ1Н- прямоугольный,
так как В1Н –высота В1Н=ВВ1*cos 600
Найти:Vпризмы=?
Решение:
Дано: АВСА1В1С1- наклонная прямая призма. <В1ВК=600 , ВС=10см, АВ=10см, АС=12см, ВВ1=8см.
В1Н=8 * √3/2 = 4√3 (см)
V=4√3 *48=192√3 (см3)
С
В1
С1 А1
В
К
Н
А

Дано:АВСДА1В1С1Д1-призма, АВСД-прямоугольник, АВ=а, АД=b, АА1=с, <А1АД=<А1АВ=ß
Найти: Vпризмы=?
Решение:
<А1АД=<А1АВ значит точка А1 проецируется на биссектрису <А, А1О ┴ (АВС), АО-биссектриса <А
Так как А1О┴(АВС) , ОМ┴АД (ОМ-проекция, А1М-наклонная) отсюда следует, А1М┴АД
Треугольник АА1М-прямоугольный, АМ=С·cosß
Треугольник АОМ-прямоугольный, АО=√2·АМ, АО=√2·С·сosß
А1О= √с2-2с2-cos2ß=с√1-2cos2ß = с√-cos2ß.
V=Sосн.·h= а·b·c√-cos2ß
Ответ : V=а·b·c√-cos2ß
А
В
С
Д
В1
А1
Д1
С1
К
М
О
№ 680 Основанием наклонной призмы является прямоугольный треугольник со сторонами а и b. Боковые ребра длины с составляет со смежными сторонами основания углы, равные ß . Найти объем призмы?