Слайд 2 Отличительная особенность игры с природой состоит в том, что в ней сознательно

действует только один из участников, в большинстве случаев называемый игроком 1.
Игрок 2 (природа) сознательно против игрока 1 не действует, а выступает как не имеющий конкретной цели и случайным образом выбирающий очередные «ходы» партнер по игре.
Поэтому термин «природа» характеризует некую объективную действительность, которую не следует понимать буквально, хотя вполне могут встретиться ситуации, в которых «игроком» 2 действительно может быть природа (например, обстоятельства, связанные с погодными условиями или с природными стихийными силами).
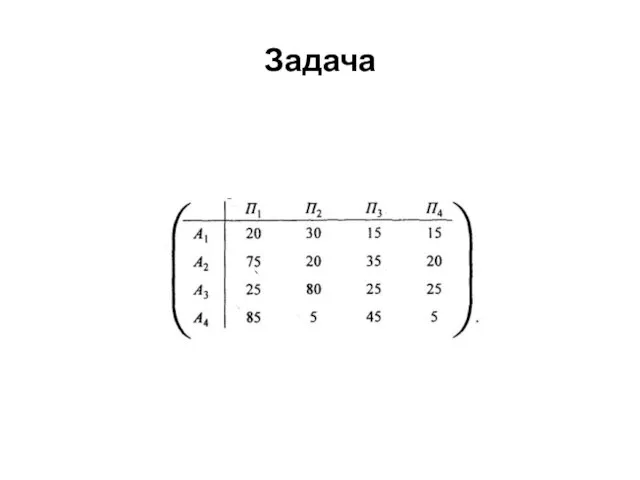
Слайд 3Задача
Необходимо закупить уголь для обогрева дома. Количество хранимого угля ограничено и в

течение холодного периода должно быть полностью израсходовано. Предполагается, что неизрасходованный зимой уголь в лето пропадает. Покупать уголь можно в любое время, однако летом он дешевле, чем зимой. Неопределенность состоит в том, что не известно, какой будет зима: суровой, тогда придется докупать уголь, или мягкой, тогда часть угля может остаться неиспользованной. Очевидно, что у природы нет злого умысла и она ничего против человека «не имеет». С другой стороны, долгосрочные прогнозы, составляемые метеорологическими службами, неточны и поэтому могут использоваться в практической деятельности только как ориентировочные при принятии решений.
Слайд 4Организация и аналитическое представление игры с природой
Пусть игрок 1 имеет т
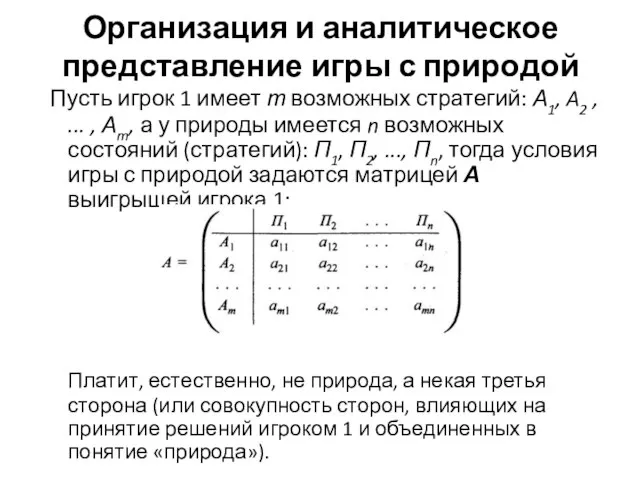
возможных стратегий: А1, A2 , ... , Аm, а у природы имеется n возможных состояний (стратегий): П1, П2, ..., Пn, тогда условия игры с природой задаются матрицей А выигрышей игрока 1:
Платит, естественно, не природа, а некая третья сторона (или совокупность сторон, влияющих на принятие решений игроком 1 и объединенных в понятие «природа»).
Слайд 5 Возможен и другой способ задания матрицы игры с природой: не в виде

матрицы выигрышей, а в виде так называемой матрицы рисков R = ||rij||m,n или матрицы упущенных возможностей. Величина риска - это размер платы за отсутствие информации о состоянии среды. Матрица R может быть построена непосредственно из условий задачи или на основе матрицы выигрышей А.
Риском rij игрока при использовании им стратегии Аi и при состоянии среды Пj будем называть разность между выигрышем, который игрок получил бы, если бы он знал, что состоянием среды будет Пj, и выигрышем, который игрок получит, не имея этой информации.
Зная состояние природы (стратегию) Пj, игрок выбирает ту стратегию, при которой его выигрыш максимальный, т.е. rij = βj – aij при заданном j. Например, для матрицы выигрышей
Слайд 6Согласно введенным определениям rij и βj получаем матрицу рисков

Слайд 7 ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ ПОЛНОЙ НЕОПРЕДЕЛЕННОСТИ
Неопределенность, связанную с отсутствием информации о

вероятностях состоянии среды (природы), называют «безнадежной» или «дурной».
В таких случаях для определения наилучших решений используются следующие критерии:
максимакса,
Вальда,
Сэвиджа,
Гурвица.
Слайд 8Критерий максимакса
С его помощью определяется стратегия, максимизирующая максимальные выигрыши для каждого состояния

природы. Это критерий крайнего оптимизма. Наилучшим признается решение, при котором достигается максимальный выигрыш, равный .
Нетрудно увидеть, что для матрицы А наилучшим решением будет А1, при котором достигается максимальный выигрыш - 9.
Следует отметить, что ситуации, требующие применения такого критерия, в экономике в общем нередки, и пользуются им не только безоглядные оптимисты, но и игроки, поставленные в безвыходное положение, когда они вынуждены руководствоваться принципом «или пан, или пропал».
Слайд 9Максиминный критерий Вальда
С позиций данного критерия природа рассматривается как агрессивно настроенный и

сознательно действующий противник типа тех, которые противодействуют в стратегических играх. Выбирается решение, для которого достигается значение
Для платежной матрицы А (3.1) нетрудно рассчитать:
• для первой стратегии (i = 1) ;
• для второй стратегии (i=2) ;
• для третьей стратегии (i=3) .
Тогда W=3 , что соответствует второй стратегии A2 игрока 1.
В соответствии с критерием Вальда из всех самых неудачных результатов выбирается лучший (W = 3). Это перестраховочная позиция крайнего пессимизма, рассчитанная на худший случай. Такая стратегия приемлема, например, когда игрок не столь заинтересован в крупной удаче, но хочет себя застраховать от неожиданных проигрышей. Выбор такой стратегии определяется отношением игрока к риску.
Слайд 10Критерий минимаксного риска Сэвиджа
Выбор стратегии аналогичен выбору стратегии по принципу Вальда с

тем отличием, что игрок руководствуется не матрицей выигрышей А , а матрицей рисков R :
Для матрицы R нетрудно рассчитать:
• для первой стратегии (i=1) ;
• для второй стратегии (i=2) ;
• для третьей стратегии (i=3) .
Минимально возможный из самых крупных рисков, равный 4, достигается при использовании первой стратегии А1.
Слайд 11Критерий пессимизма-оптимизма Гурвица
Этот критерий при выборе решения рекомендует руководствоваться некоторым средним результатом,

характеризующим состояние между крайним пессимизмом и безудержным оптимизмом. Согласно этому критерию стратегия в матрице А выбирается в соответствии со значением
При p = 0 критерий Гурвица совпадает с максимаксным критерием, а при р = 1 - с критерием Вальда. Покажем процедуру применения данного критерия для матрицы А при р = 0,5:
Слайд 13Применительно к матрице рисков R критерий пессимизма-оптимизма Гурвица имеет вид:
При р =

0 выбор стратегии игрока 1 осуществляется по условию наименьшего из всех возможных рисков ( ); при р = 1 - по критерию минимаксного риска Сэвиджа.
Слайд 15 ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ РИСКА
Когда состояниям природы поставлены в соответствие вероятности,

заданные экспертно либо вычисленные, решение обычно принимается на основе критерия максимума ожидаемого среднего выигрыша или минимума ожидаемого среднего риска
Если для некоторой игры с природой, задаваемой платежной матрицей А = ||aij||m,n, стратегиям природы Пj соответствуют вероятности рj, то лучшей стратегией игрока 1 будет та, которая обеспечивает ему максимальный средний выигрыш, т.е.













 Логарифмические уравнения
Логарифмические уравнения Прямоугольные треугольники
Прямоугольные треугольники ЕГЭ. Математика. Задание № 5. Решение простейших тригонометрических уравнений
ЕГЭ. Математика. Задание № 5. Решение простейших тригонометрических уравнений Математическая разминка (4 класс)
Математическая разминка (4 класс) Викторина по математике, 1 класс
Викторина по математике, 1 класс Практическое занятие №7 Минимизация логического автомата
Практическое занятие №7 Минимизация логического автомата Умножение обыкновенных дробей
Умножение обыкновенных дробей Признаки равенства треугольников. Равнобедренный треугольник. Задачи по готовым чертежам
Признаки равенства треугольников. Равнобедренный треугольник. Задачи по готовым чертежам Математические основы ТАУ (продолжение)
Математические основы ТАУ (продолжение) Дифференциальные уравнения
Дифференциальные уравнения Конкурсное задание УРОК
Конкурсное задание УРОК Метод линейного сплайна
Метод линейного сплайна Случайные погрешности. Вероятностное описание результатов и погрешностей
Случайные погрешности. Вероятностное описание результатов и погрешностей Вычисление неопределенного интеграла
Вычисление неопределенного интеграла Свойства предметов. Сравнение предметов по форме, размеру, цвету, материалу
Свойства предметов. Сравнение предметов по форме, размеру, цвету, материалу Занимательная геометрия (1 класс)
Занимательная геометрия (1 класс) Сложение с переходом через десяток вида +6, +7. Считаем с гномами
Сложение с переходом через десяток вида +6, +7. Считаем с гномами Случайность. Массовые явления
Случайность. Массовые явления Методы решения задач на смеси и сплавы
Методы решения задач на смеси и сплавы Умножение. Законы умножения
Умножение. Законы умножения График функции. Тест, 1-6 варианты
График функции. Тест, 1-6 варианты Множество и его элементы
Множество и его элементы Экскурсия в мир чисел
Экскурсия в мир чисел Комбинаторика
Комбинаторика Коэффициенты линейной функции
Коэффициенты линейной функции Элементы векторной алгебры
Элементы векторной алгебры Понятие множество
Понятие множество Что такое дискретная математика?
Что такое дискретная математика?