Содержание
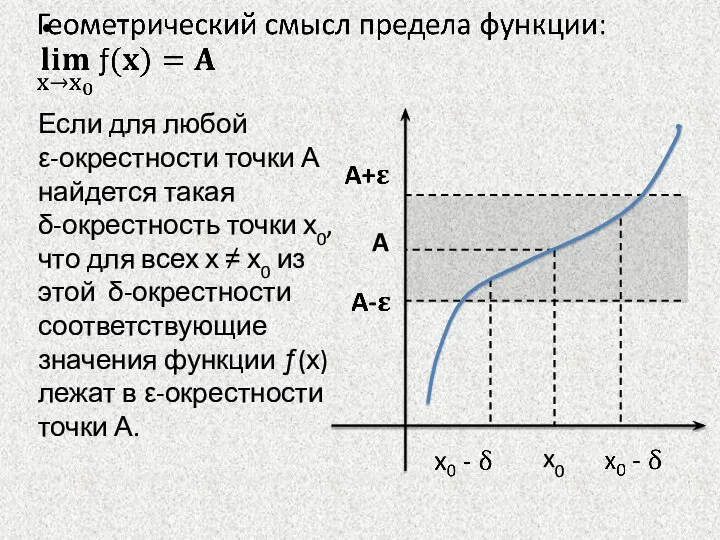
- 2. §3. ПРЕДЕЛ ФУНКЦИИ 3.1. Предел функции в точке Число А называется пределом функции в точке х0
- 3. Если для любой ε-окрестности точки А найдется такая δ-окрестность точки х0, что для всех х ≠
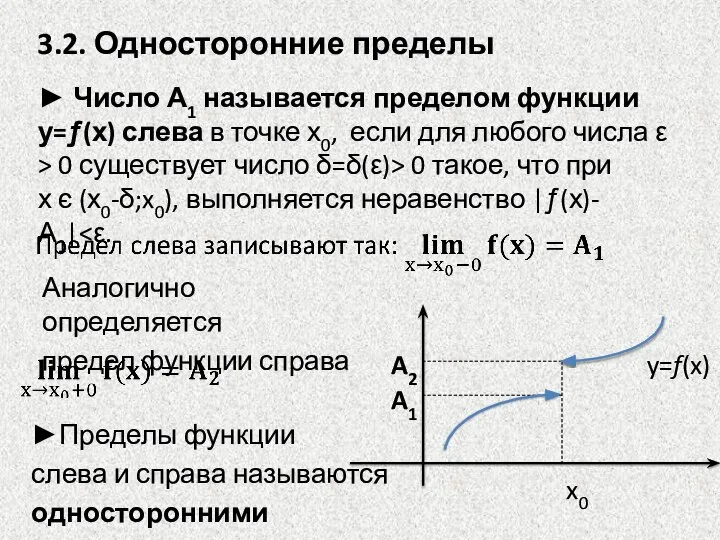
- 4. 3.2. Односторонние пределы ► Число А1 называется пределом функции у=ƒ(х) слева в точке х0, если для
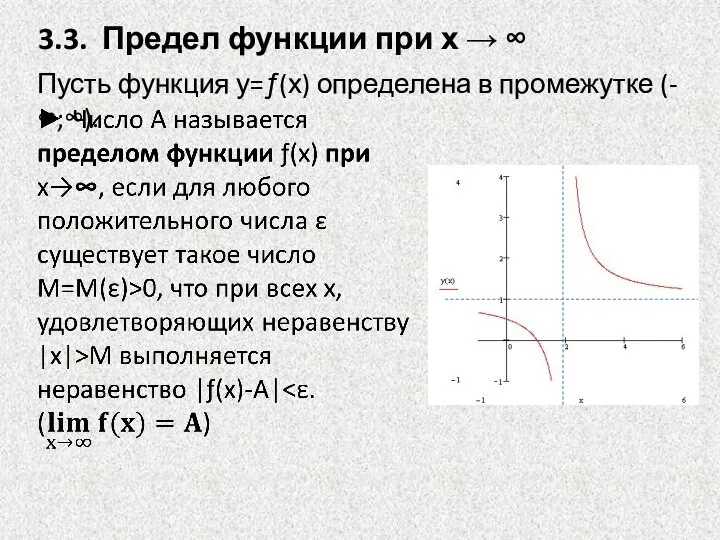
- 5. 3.3. Предел функции при х → ∞ Пусть функция у=ƒ(х) определена в промежутке (-∞;∞).
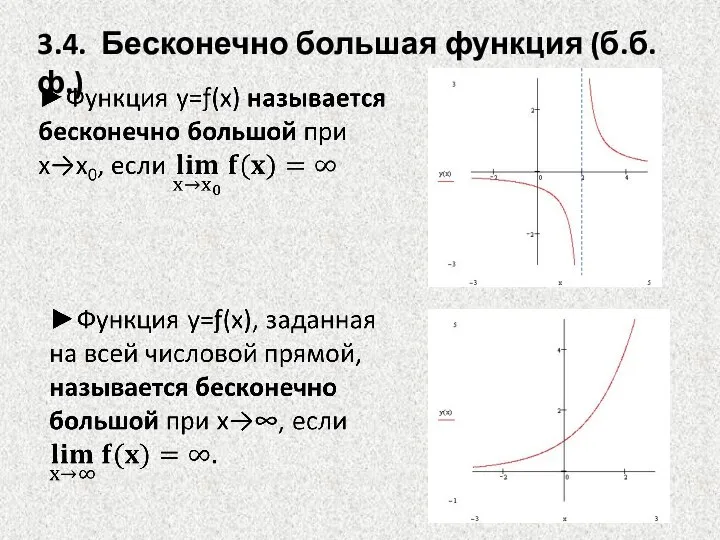
- 6. 3.4. Бесконечно большая функция (б.б.ф.)
- 7. 3.5.1. Определения и основные теоремы Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми.
- 8. Теорема 1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция. Теорема 2. Произведение
- 9. Теорема 3. Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть
- 10. 3.5.2. Связь между функцией, ее пределом и бесконечно малой функцией
- 11. §4. Основные теоремы о пределах Следствие. Функция может иметь только один предел при х→х0.
- 13. §5. Основные способы вычисления пределов. Алгоритм решения. Подставить в выражение предельное значение аргумента. Определить есть или
- 14. Способ 1. Применение формул(нахождение корней квадратного уравнения, формулы сокращенного умножения, тригонометрические формулы).
- 17. Способ 4. Первый замечательный предел
- 18. Способ 5. Второй замечательный предел Примеры:
- 19. Задача о непрерывном начислении процентов A0 – первоначальный вклад в банк. Найдем размер вклада A1 через
- 20. Формула может быть использована при непрерывном вычислении процентов
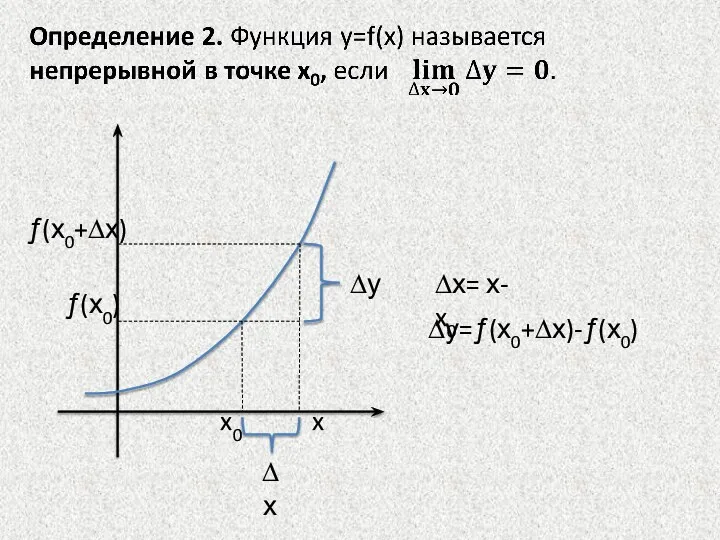
- 21. §6. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ 6.1. Непрерывность функции в точке Пусть функция у=ƒ(х) определена в точке х0 и
- 22. ∆х= х- x0 ∆у=ƒ(х0+∆х)-ƒ(х0)
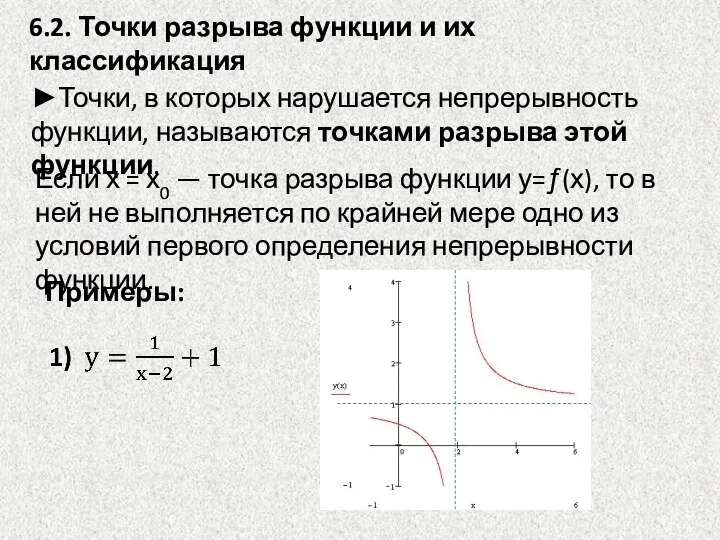
- 23. 6.2. Точки разрыва функции и их классификация ►Точки, в которых нарушается непрерывность функции, называются точками разрыва
- 25. Все точки разрыва функции разделяются на точки разрыва первого и второго рода. а) если А1=А2, то
- 27. Скачать презентацию


















 Геометрическая прогрессия
Геометрическая прогрессия Probability Distributions
Probability Distributions Логарифмическая функция
Логарифмическая функция Аксиомы стереометрии и их следствия
Аксиомы стереометрии и их следствия Морское путешествие
Морское путешествие Разложение многочлена на множители способом группировки. 7 класс
Разложение многочлена на множители способом группировки. 7 класс Счет и вычисления основа порядка в голове. (Песталоцци)
Счет и вычисления основа порядка в голове. (Песталоцци) Тождественные преобразования. 7 класс
Тождественные преобразования. 7 класс Математика. Учебный 2022 год с Марусей
Математика. Учебный 2022 год с Марусей Графический способ решения систем уравнений. Свойства графиков функций
Графический способ решения систем уравнений. Свойства графиков функций Число 0. Цифра 0
Число 0. Цифра 0 Сложение смешанных дробей
Сложение смешанных дробей Спрощення виразів. Підготовка до ЗНО
Спрощення виразів. Підготовка до ЗНО Арифметическая прогрессия. Обобщающий урок
Арифметическая прогрессия. Обобщающий урок Презентация на тему Применение распределительного свойства умножения 6 класс
Презентация на тему Применение распределительного свойства умножения 6 класс  Решение неравенств
Решение неравенств Преобразование обыкновенных дробей в десятичные
Преобразование обыкновенных дробей в десятичные Производная и дифференциал функции
Производная и дифференциал функции Simple Affirmative Negative Speaking
Simple Affirmative Negative Speaking Производная функции
Производная функции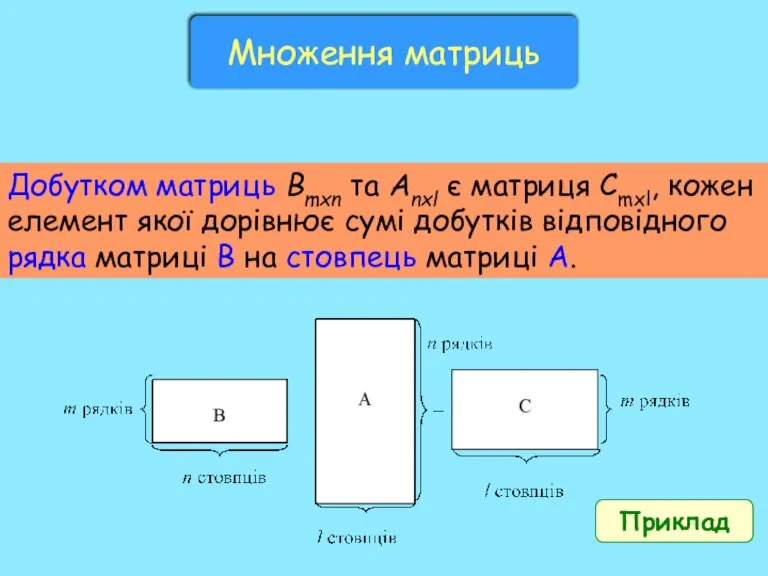 Множення матриць
Множення матриць Презентация на тему ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ
Презентация на тему ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ  Пропорциональность величин
Пропорциональность величин Решение уравнений с переменной под знаком модуля
Решение уравнений с переменной под знаком модуля Ромб та його властивості
Ромб та його властивості Страничка для любознательных
Страничка для любознательных Урок повторения
Урок повторения Финансовая математика: банки, вклады, кредиты. Часть 2
Финансовая математика: банки, вклады, кредиты. Часть 2