Четыре замечательные точки треугольника

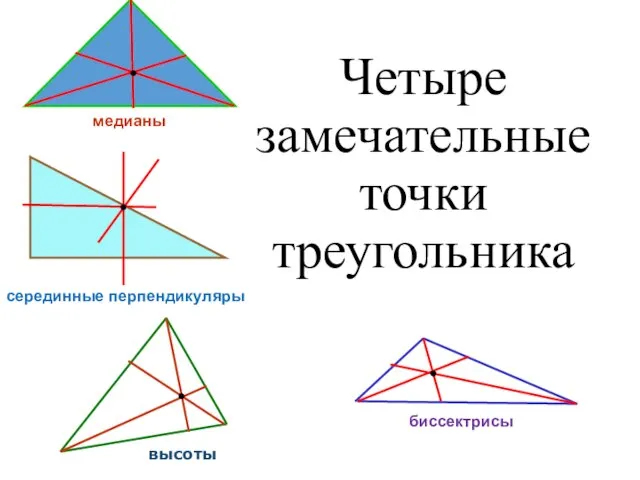
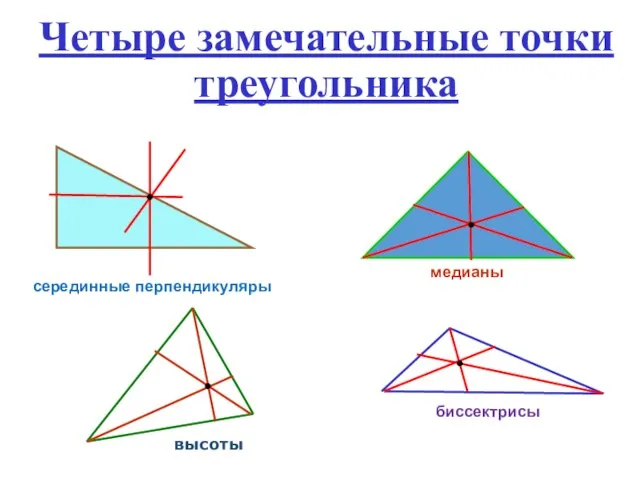
Четыре замечательные точки треугольника
высоты
биссектрисы
серединные перпендикуляры
медианы

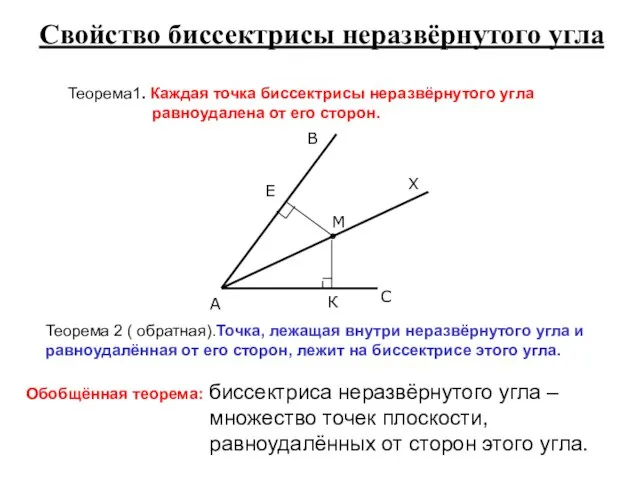
Свойство биссектрисы неразвёрнутого угла
Теорема1. Каждая точка биссектрисы неразвёрнутого угла
равноудалена от его сторон.
Теорема 2 ( обратная).Точка, лежащая внутри неразвёрнутого угла и равноудалённая от его сторон, лежит на биссектрисе этого угла.
Обобщённая теорема: биссектриса неразвёрнутого угла –
множество точек плоскости,
равноудалённых от сторон этого угла.

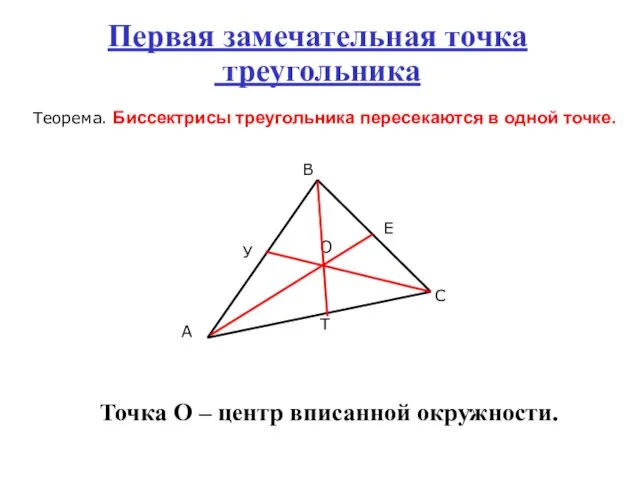
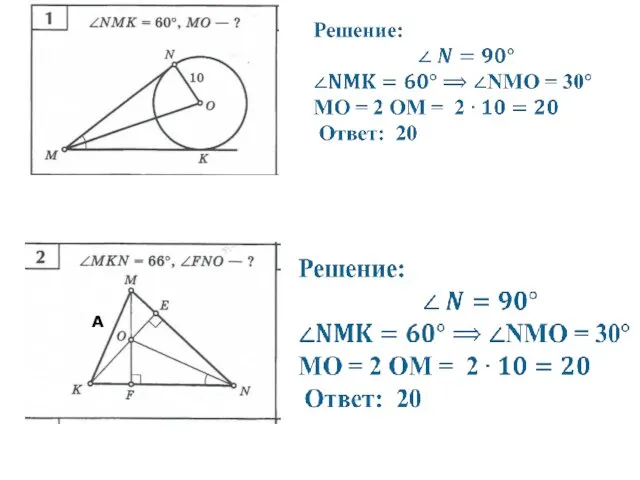
Первая замечательная точка
треугольника
Теорема. Биссектрисы треугольника пересекаются в одной точке.
Точка О – центр вписанной окружности.

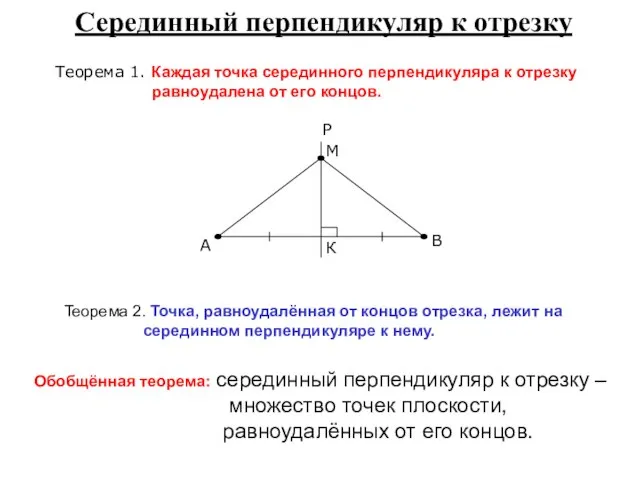
Серединный перпендикуляр к отрезку
Теорема 1. Каждая точка серединного перпендикуляра к отрезку
равноудалена от его концов.
Теорема 2. Точка, равноудалённая от концов отрезка, лежит на
серединном перпендикуляре к нему.
Обобщённая теорема: серединный перпендикуляр к отрезку –
множество точек плоскости,
равноудалённых от его концов.

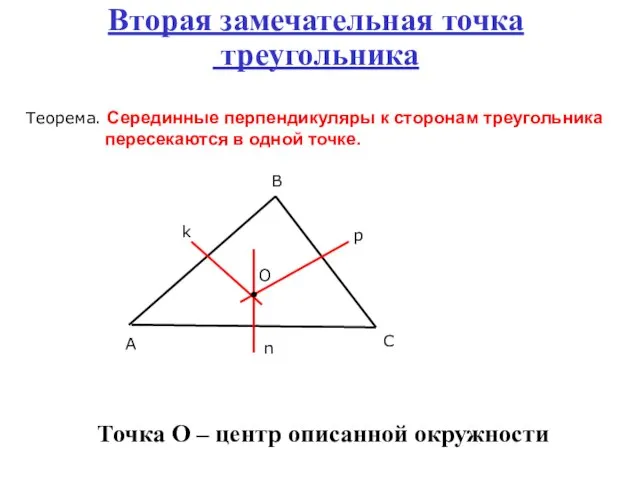
Вторая замечательная точка
треугольника
Теорема. Серединные перпендикуляры к сторонам треугольника
пересекаются в одной точке.
Точка О – центр описанной окружности

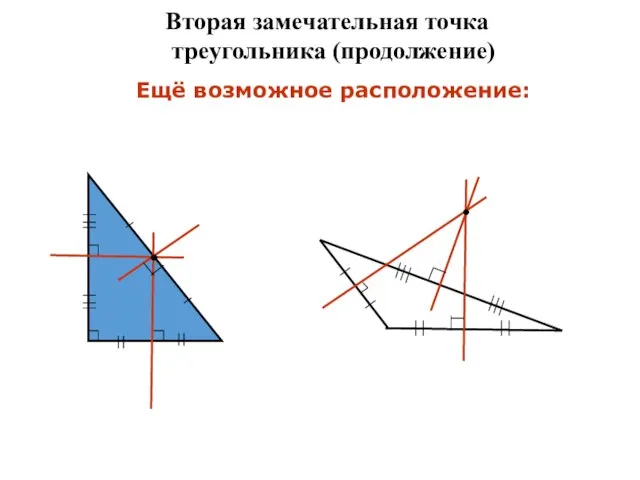
Вторая замечательная точка
треугольника (продолжение)
Ещё возможное расположение:

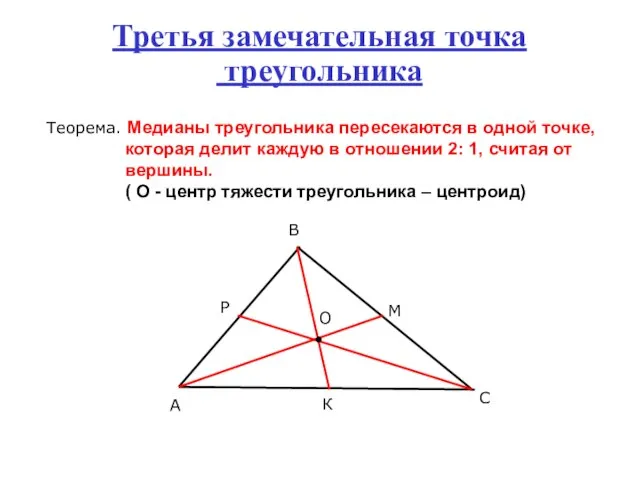
Третья замечательная точка
треугольника
Теорема. Медианы треугольника пересекаются в одной точке,
которая делит каждую в отношении 2: 1, считая от
вершины.
( О - центр тяжести треугольника – центроид)

Треугольник, который опирается на острие иглы в точке пересечения медиан, находится в равновесии!
Точка пересечения медиан называется
центром тяжести треугольника.

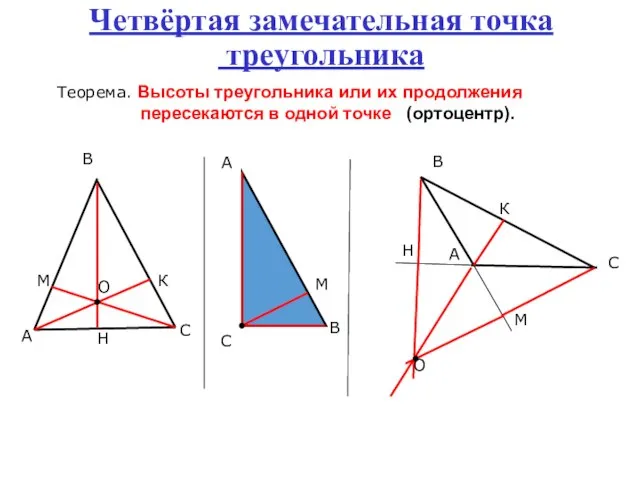
Четвёртая замечательная точка
треугольника
Теорема. Высоты треугольника или их продолжения
пересекаются в одной точке (ортоцентр).

Четыре замечательные точки треугольника
высоты
биссектрисы
серединные перпендикуляры
медианы

А