Метод Ньютона

Метод Ньютона
Таким образом, следующее приближение к корню будет
Это итерационная схема носит название метода Ньютона (или метода касательных)

Метод Ньютона
Уравнение касательной:
Для y=0 значение х будет равно х1:
Находим x1:

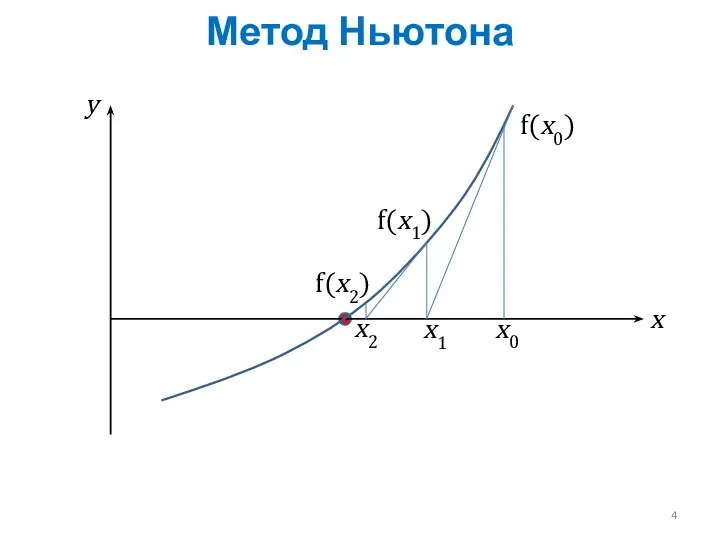
Метод Ньютона
x0
x
y
f(x0)
x1
f(x1)
x2
f(x2)

Метод Ньютона
Условие сходимости метода Ньютона
Т.к.

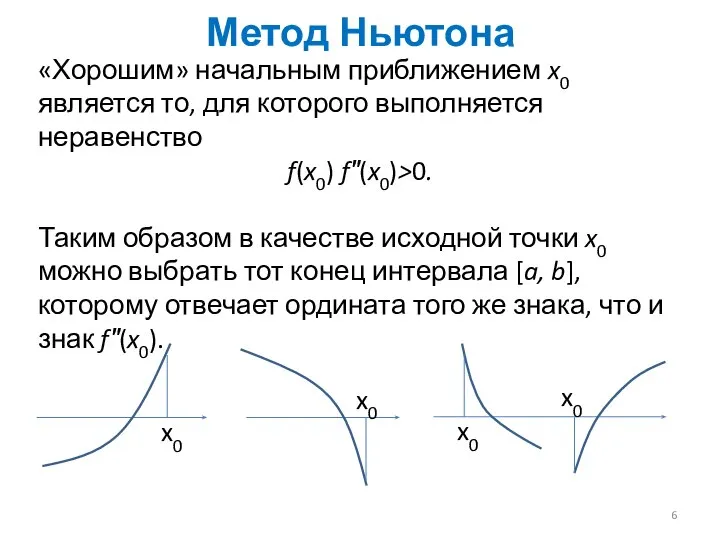
Метод Ньютона
«Хорошим» начальным приближением x0 является то, для которого выполняется неравенство
f(x0) f″(x0)>0.
Таким образом в качестве исходной точки x0 можно выбрать тот конец интервала [a, b], которому отвечает ордината того же знака, что и знак f″(x0).
x0
x0
x0
x0

Метод Ньютона
Примеры «плохого» поведения метода Ньютона

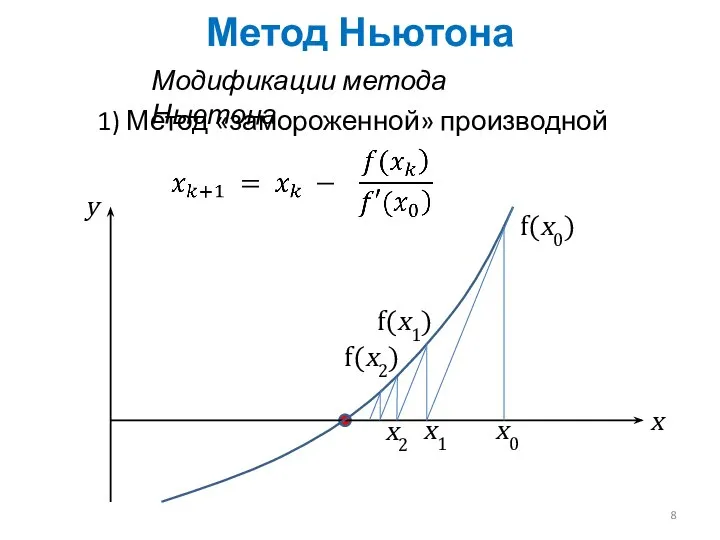
Метод Ньютона
Модификации метода Ньютона
1) Метод «замороженной» производной
x0
x
y
f(x0)
x1
f(x1)
x2
f(x2)

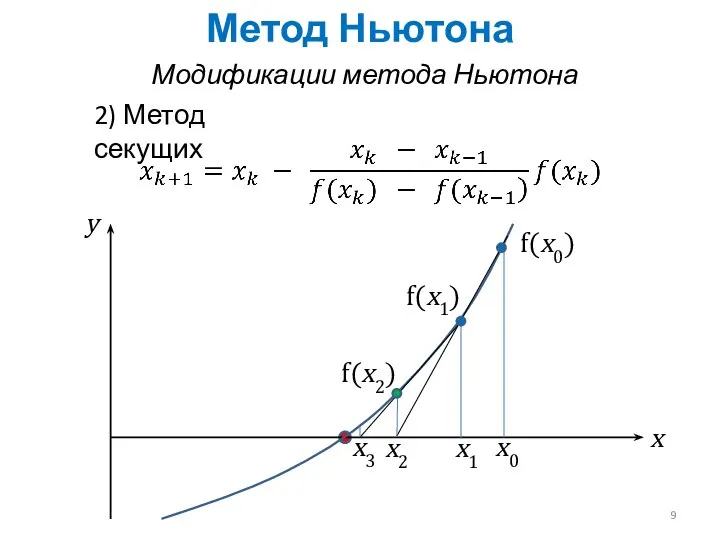
Метод Ньютона
Модификации метода Ньютона
2) Метод секущих
x0
x
y
f(x0)
x1
f(x1)
x2
f(x2)
x3

Метод Чебышева построения итераций
высших порядков
Пусть уравнение y = f(x) = 0 на [a, b] имеет корень х*.
Пусть f′(x) ≠ 0. Функция y = f(x) имеет обратную функцию x = F(y) и x ≡ F(f(x)).
Тогда

Метод Чебышева построения итераций
высших порядков
Можно записать, что
Следовательно, итерационная схема будет иметь вид

Метод Чебышева построения итераций
высших порядков
Дифференцируем соотношение
Дифференцируем соотношение еще раз

Метод Чебышева построения итераций
высших порядков
И т.д.
Частные случаи
j=1
– формула Ньютона

j=2
Метод Чебышева построения итераций
высших порядков

Скорость сходимости методов

Нахождение корней полиномов
Рассмотренные выше методы решения нелинейных трансцендентных уравнений пригодны и для алгебраических уравнений.
Особенности нахождения корней полиномов.
1) Неустойчивость корней некоторых полиномов как функций от их коэффициентов, что предъявляет особые требования к точности вычислений.
Pn(x) = anxn + an–1xn–1 +… + a1x + a0

Нахождение корней полиномов
2) Полином степени n имеет ровно n корней, действительных или комплексных, при условии, что каждый корень считается столько раз, какова его кратность.
3) Комплексные корни образуют комплексно-сопряженные пары, т.е. каждому корню
x = c + id соответствует x = c – id.
4) Известны оценки границ корней полинома:
r < |xk| < R

Нахождение корней полиномов
1) Это завышенные оценки.
2) В связи с малостью r на практике пользуются
оценкой |xk| < R.
3) Эти оценки справедливы и для комплексных корней.

Нахождение корней полиномов
Pn(x) = anxn + an–1xn–1 +… + a1x + a0

Нахождение корней полиномов
Как быть, если рассматриваемое уравнение имеет комплексные корни?
1) Если все значения функции вещественны и в качестве начального приближения x0 также взято вещественное число, то и все последующие значения xk также будут вещественны.
2) Однако если взять в качестве x0 комплексное число, то последующие xk могут оказаться комплексными.
3) Если найден один комплексный корень x1 = c + id , то всегда будет существовать сопряженный ему корень
x2 = c – id.

Нахождение корней полиномов
Если многочлен Pn(x) имеет пару комплексно-сопряженных корней x1,2 = c ± id, то его можно записать в следующем виде: Pn(x) = (x–x1)( x–x2) Pn–2(x)
или Pn(x) = ((x–с)2+d2)Pn–2(x)
Дальше можно решать уравнение Pn–2(x) = 0
вместо Pn(x) = 0.

Решение систем нелинейных уравнений

Метод простых итераций
Представим исходную систему уравнений в виде:

Метод простых итераций
Матрица Якоби:

Метод простых итераций

Скорость сходимости выше, чем в методе простых итераций.

Метод Ньютона
Этот метод обладает гораздо более быстрой сходимостью, чем метод простых итераций.
Недостатки:
Очень важен удачный выбор начального приближения для обеспечения хорошей сходимости;
Сходимость ухудшается с увеличением числа уравнений системы.

Метод Ньютона

Метод Ньютона

Метод Ньютона
– матрица Якоби, составленная из частных производных:

Метод Ньютона
Чтобы найти следующее приближение x(1) к решению системы f(x)=0, решаем систему уравнений:

Метод Ньютона
Для нахождения приближения x(k) , решаем систему уравнений:
Эту систему можно переписать для поправки Δx(k+1)= x(k+1) – x(k)

Метод Ньютона
Решение можно записать и в другом виде – непосредственно для x(k+1):
Еще одно ограничение, накладываемое на метод Ньютона: определитель матрицы Якоби должен быть отличен от нуля.

Метод Ньютона для решения системы
2-х уравнений
Матрица Якоби:

Метод Ньютона для решения системы
2-х уравнений

Метод Ньютона для решения системы
2-х уравнений
Уравнение
записывается в виде: