5.0 Простейшие задачи в координатах

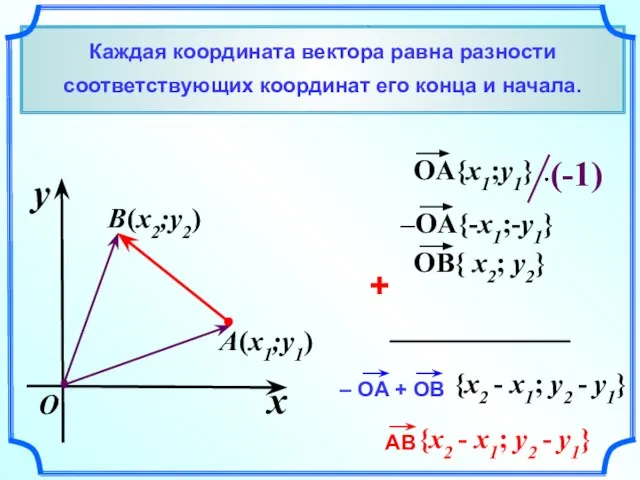
Каждая координата вектора равна разности
соответствующих координат его конца и начала.
x
y
O
(x1;y1)
(x2;y2)
{x2 - x1; y2 - y1}

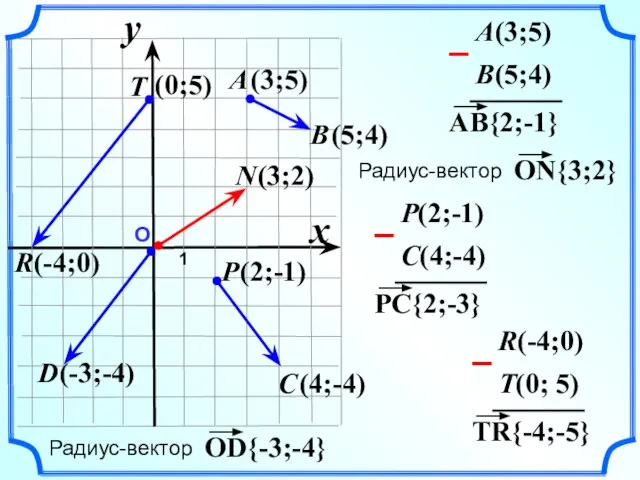
О
1
x
y
B(5;4)
A(3;5)
C(4;-4)
P(2;-1)
T(0; 5)
R(-4;0)

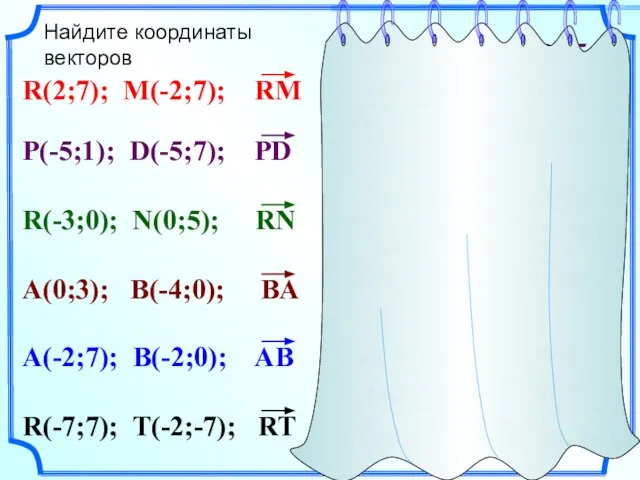
Найдите координаты
векторов
R(2; 7)
M(-2;7)
P(-5; 1)
D(-5;7)
R(-3;0)
N(0; 5)
B(-4;0)
A(0; 3)
A(-2;7)
B(-2;0)
R(-7; 7)
T(-2;-7)

B(5; 4)
A(x; y)
5 – x = 2
x = 3
4 – y = -1
y = 5
Обратные задачи.
B(x; y)
A(2;-4)
x – 2 = 2
x = 4
y + 4= -1
y = -5

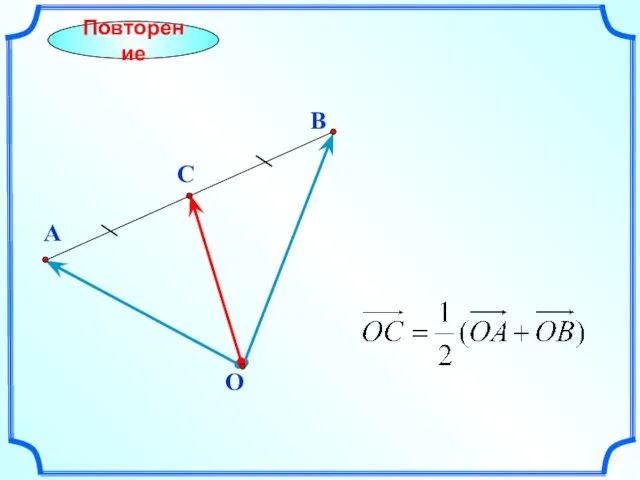
B
Повторение
A

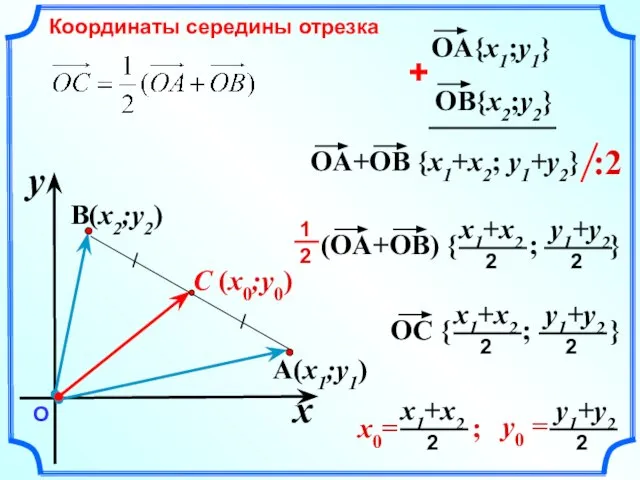
C (x0;y0)
A(x1;y1)
B(x2;y2)
x
y
О
Координаты середины отрезка

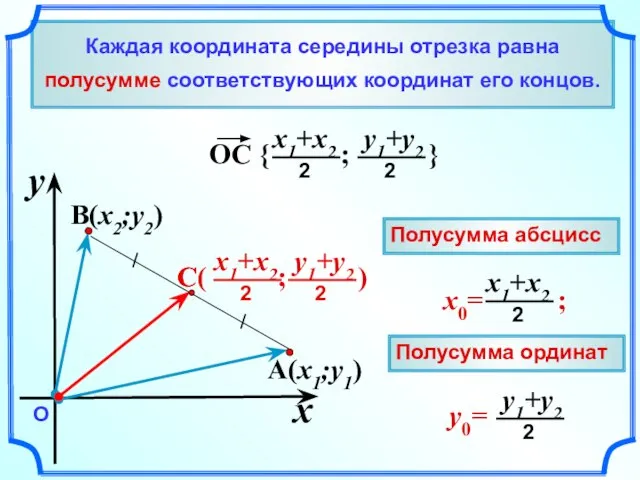
Каждая координата середины отрезка равна
полусумме соответствующих координат его концов.
A(x1;y1)
B(x2;y2)
x
y
О
Полусумма абсцисс
Полусумма ординат
C

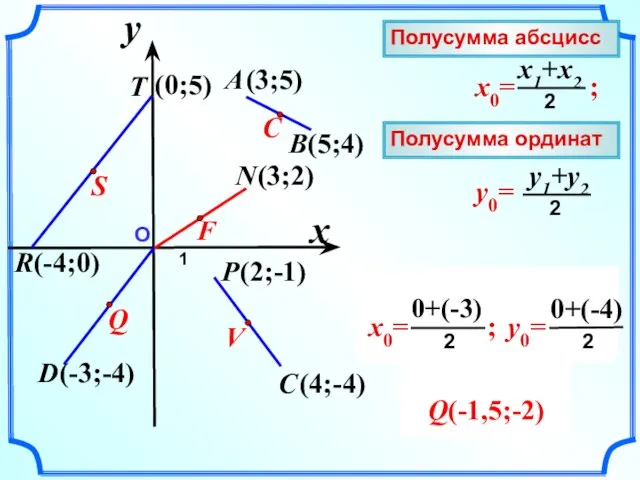
О
1
x
y
A
(3;5)
B(5;4)
Полусумма абсцисс
Полусумма ординат

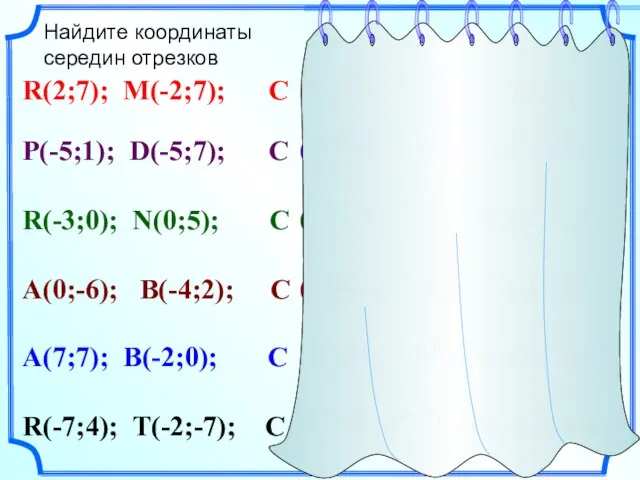
Найдите координаты
cередин отрезков
R(2;7); M(-2;7); C
P(-5;1); D(-5;7); C
R(-3;0); N(0;5); C
A(0;-6); B(-4;2); C
R(-7;4); T(-2;-7); C
A(7;7); B(-2;0); C
( ; );
2
2+(-2)
2
7 + 7
C(0; 7)
C(-5; 4)
C(-1,5; 2,5)
C(-2;-2)
C(2,5; 3,5)
C(-4,5;-1,5)

Дано:
Найти:
A(5; 4); C(-3; 2) – середина отрезка AB
B(x; y)
Обратная задача.
– 6 = 5 + x
x = – 11
4 = 4 + y
y = 0
B(-11; 0)

=
=
x
y
О
Вычисление длины вектора по его координатам
OA2=OA12 + AA12
OA2= x2 + y2

Расстояние между двумя точками
M2(x2;y2)
M1(x1;y1)
d

№ 940 Найдите расстояние между точками
A(2;7) и B(-2;7)
1 способ
2 способ
B(-2; 7)
A( 2; 7)
1)
2)

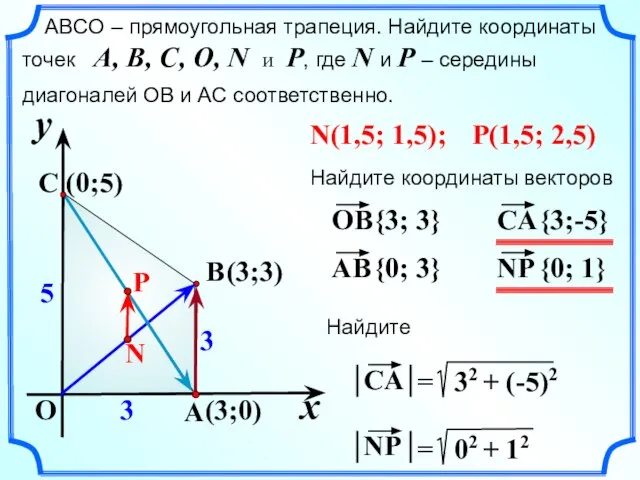
x
y
O
A
C
B
5
3
3
ABCО – прямоугольная трапеция. Найдите координаты точек A, B, C, O, N и P, где N и P – середины
диагоналей OB и AC соответственно.
(3;3)
(0;5)
N(1,5; 1,5);
P(1,5; 2,5)
(3;0)
{3; 3}
{0; 3}
{3;-5}
{0; 1}