Сборник по подготовке к государственной итоговой аттестации по геометрии

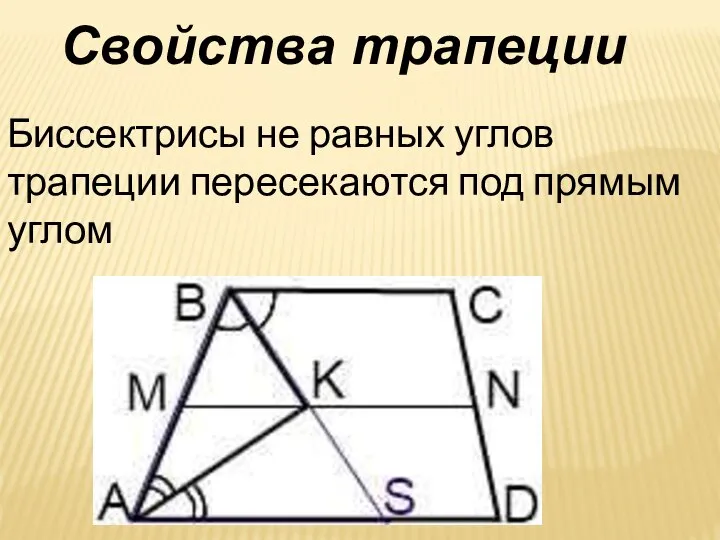
Свойства трапеции
Биссектрисы не равных углов трапеции пересекаются под прямым углом

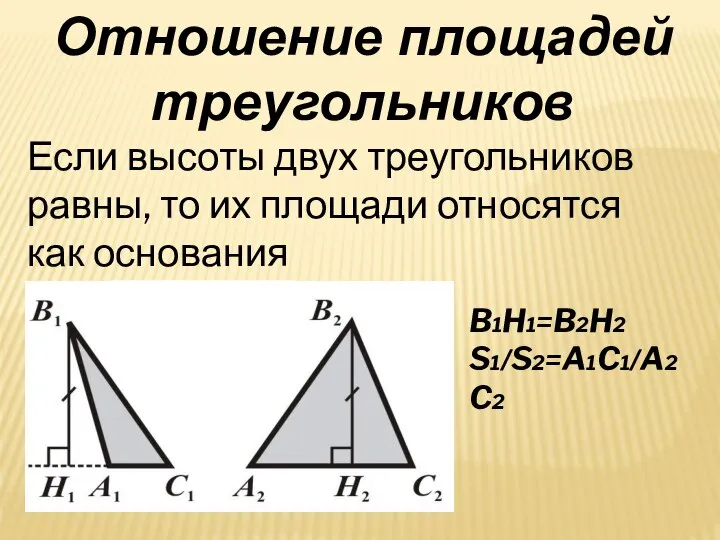
Если высоты двух треугольников равны, то их площади относятся как основания
B1H1=B2H2
S1/S2=A1C1/A2C2
Отношение площадей треугольников

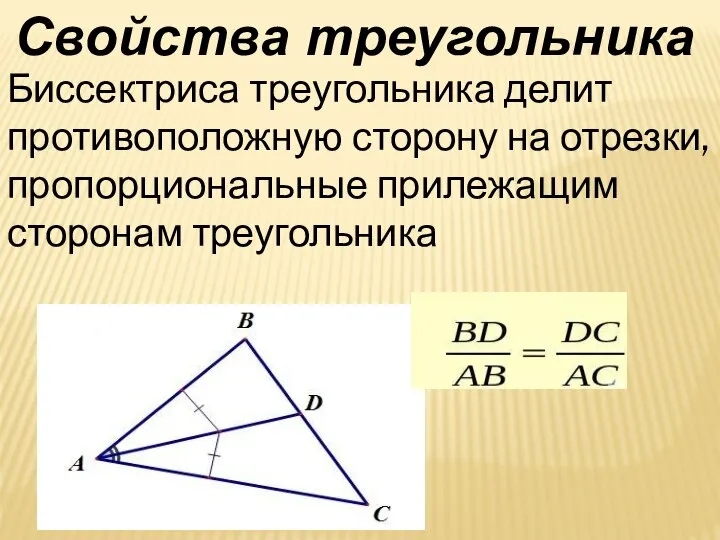
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Свойства треугольника

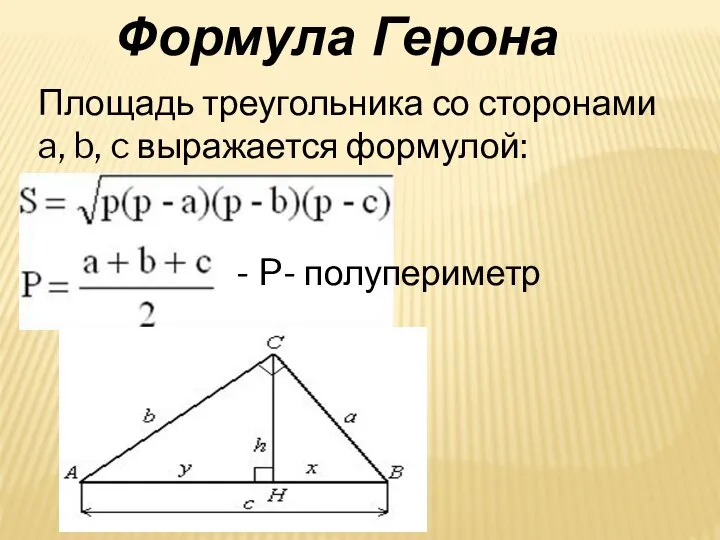
Площадь треугольника со сторонами a, b, c выражается формулой:
-
- P- полупериметр
Формула Герона

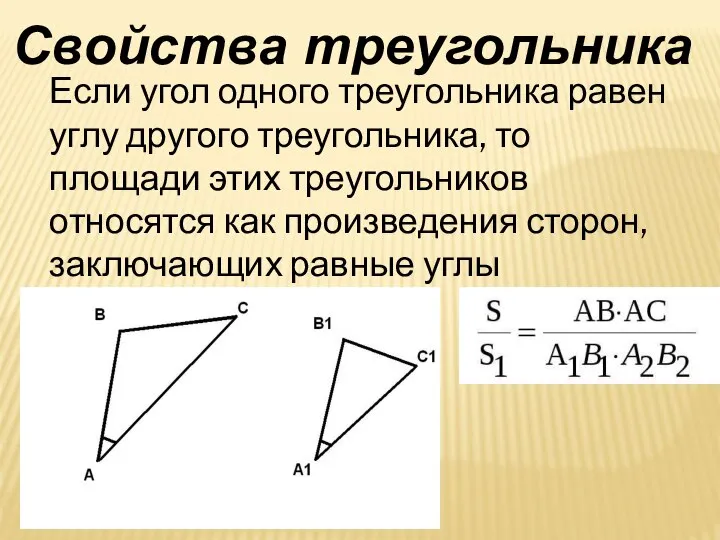
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы
Свойства треугольника

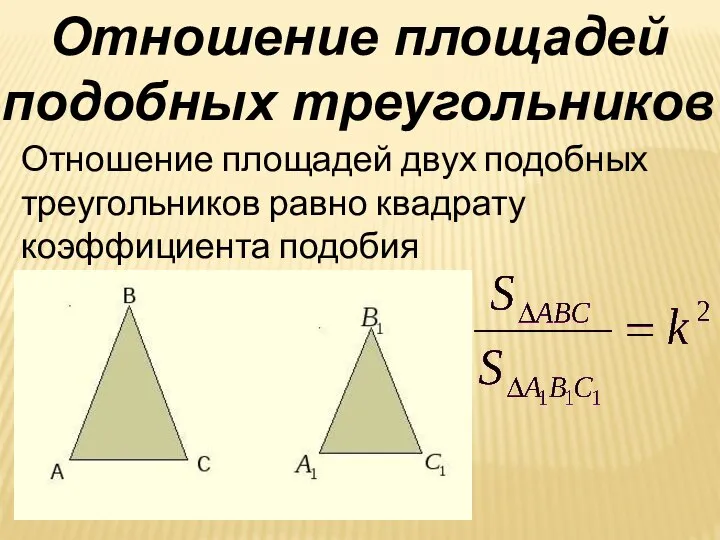
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия
Отношение площадей подобных треугольников

Отрезок XY называется средним пропорциональным (или средним геометрическим) для отрезков AB и CD, если
1 утверждение
2 утверждение
Средние пропорциональное

1 утверждение
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высоты

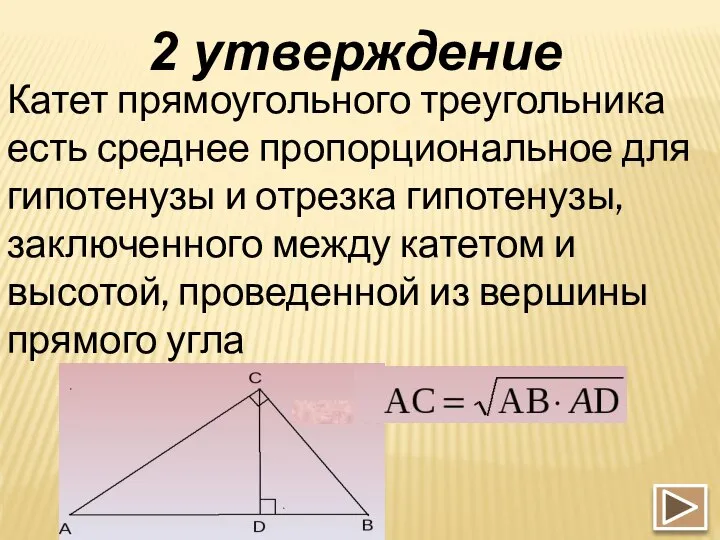
2 утверждение
Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла

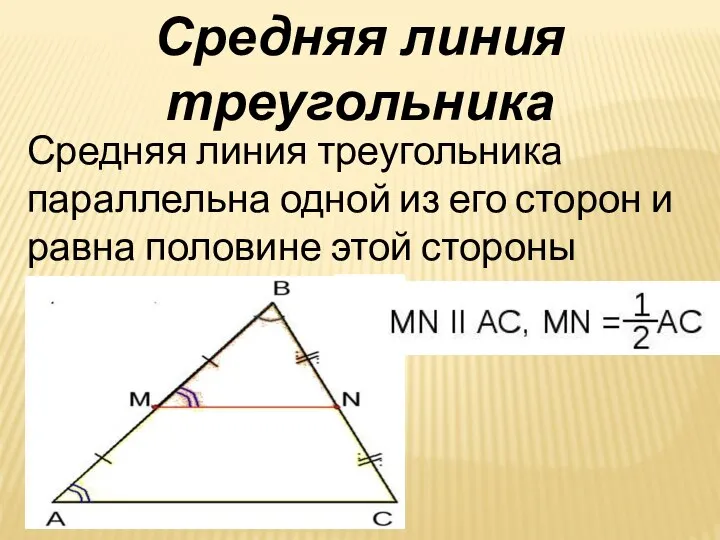
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны
Средняя линия треугольника

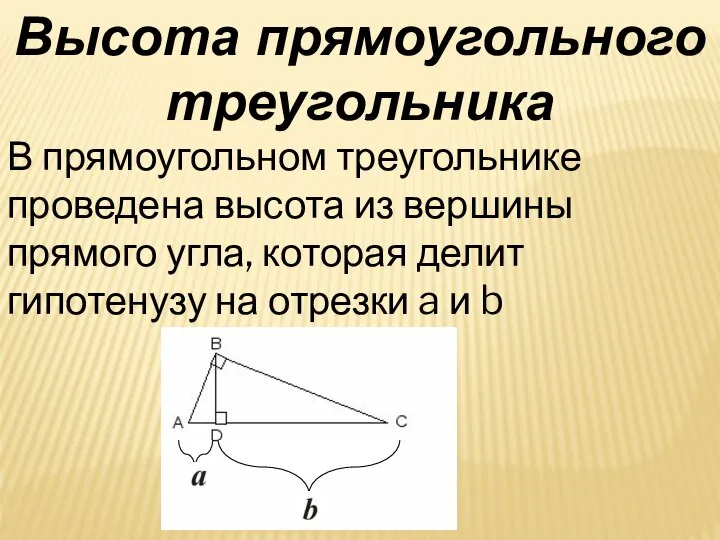
Высота прямоугольного треугольника
В прямоугольном треугольнике проведена высота из вершины прямого угла, которая делит гипотенузу на отрезки a и b

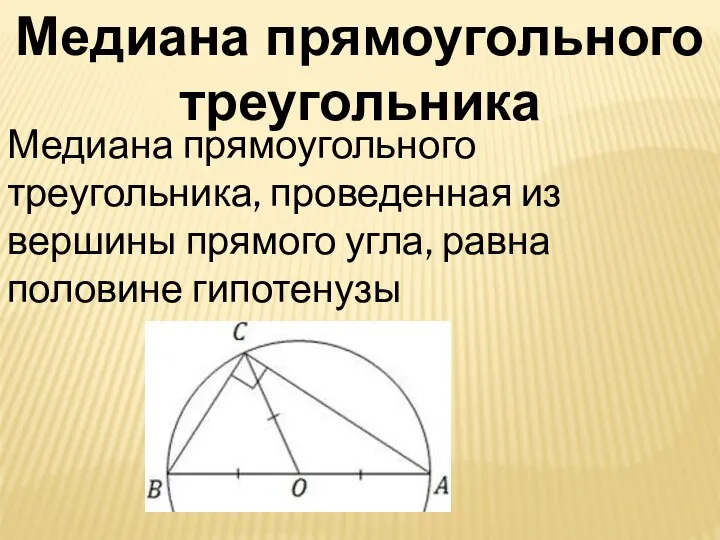
Медиана прямоугольного треугольника
Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы