Содержание
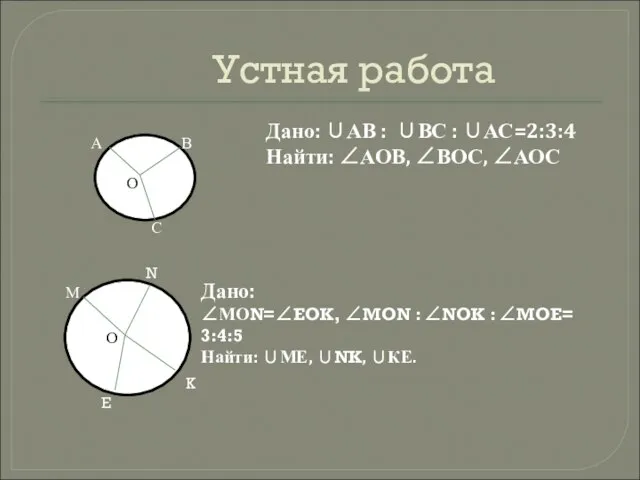
- 2. Устная работа Дано: ∪АВ : ∪ВС : ∪АС=2:3:4 Найти: ∠АОВ, ∠ВОС, ∠АОС Дано: ∠МОN=∠EOK, ∠MON :
- 3. Угол вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. Вписанный ∠ АВС
- 4. Вписанный угол измеряется половиной дуги на которую он опирается Пусть ∠ АВС – вписанный угол окружности
- 5. Рассмотрим 1 случай расположения луча ВО относительно ∠ АВС. Например луч совпадает со стороной ВС в
- 6. Рассмотрим 2 случай, когда луч ВО делит ∠ АВС на два угла. В этом случае луч
- 7. Рассмотрим 3 случай расположения луча ВО относительно ∠ АВС АВD− равнобедренный, ∠ AOD - внешний,
- 8. РАССМОТРИМ 1 СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ Вписанные углы , опирающиеся на одну и ту же дугу, равны.
- 10. Скачать презентацию






 Виды кривых, замечательные кривые. Окружность и круг
Виды кривых, замечательные кривые. Окружность и круг Пропорция
Пропорция Умники и умницы. Викторина по математике
Умники и умницы. Викторина по математике Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей Параллельные плоскости
Параллельные плоскости Викторина по математике: Где логика?
Викторина по математике: Где логика? Распределительное свойство
Распределительное свойство Математическая логика
Математическая логика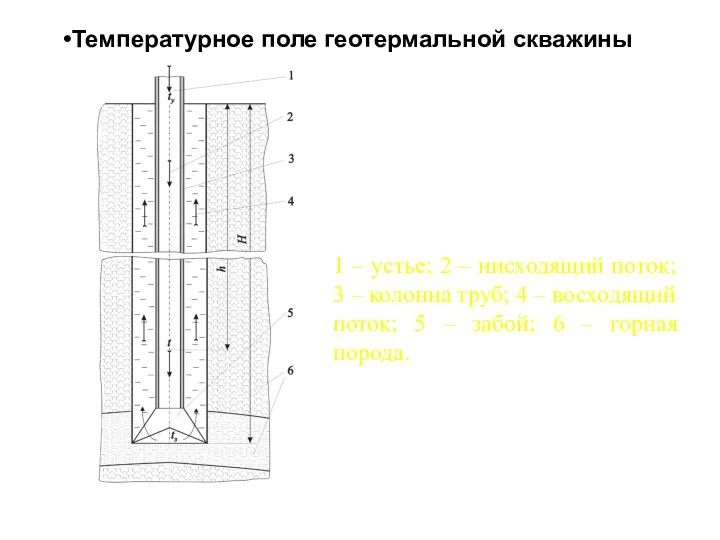 Температурное поле геотермальной скважины
Температурное поле геотермальной скважины Сумма углов треугольника
Сумма углов треугольника Тақырып 3 Минорлар және алгебралық толықтауыштар
Тақырып 3 Минорлар және алгебралық толықтауыштар Окружность. Основные теоремы
Окружность. Основные теоремы Подготовка к ЕГЭ. вычисление значений производной. В8
Подготовка к ЕГЭ. вычисление значений производной. В8 Презентация на тему Конус. Сечение конуса плоскостями
Презентация на тему Конус. Сечение конуса плоскостями 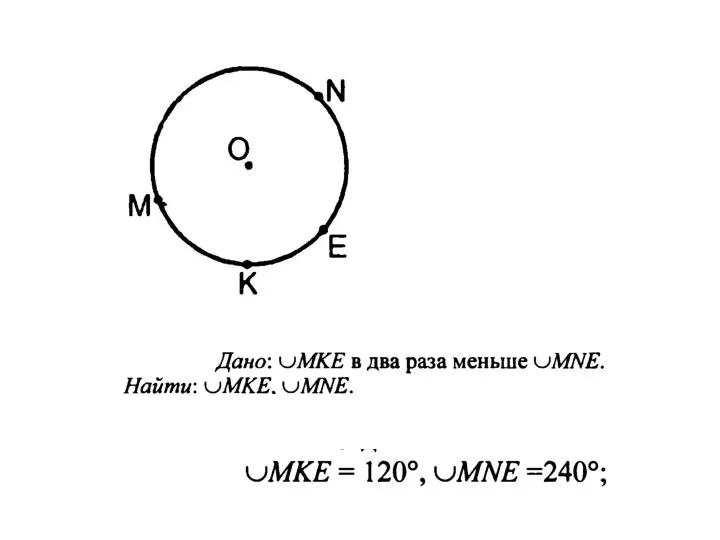 Теорема о вписанном угле
Теорема о вписанном угле Формулы сокращённого умножения: квадрат разности и квадрат суммы
Формулы сокращённого умножения: квадрат разности и квадрат суммы Реляционная алгебра
Реляционная алгебра Самостоятельная работа учащихся на уроках математики. Дудоладова М.П. Сообщение на педсовете
Самостоятельная работа учащихся на уроках математики. Дудоладова М.П. Сообщение на педсовете Статистмческие методы
Статистмческие методы Материальная точка. Система отсчета
Материальная точка. Система отсчета Повторение вычисления двухзначных чисел столбиком с переходом через десяток
Повторение вычисления двухзначных чисел столбиком с переходом через десяток Презентация на тему Треугольники (5 класс)
Презентация на тему Треугольники (5 класс)  Сфера и шар
Сфера и шар Основы теории MOM метода. Настройка параметров EM симулятора на основе метода MOM
Основы теории MOM метода. Настройка параметров EM симулятора на основе метода MOM Пирамида. Элементы пирамиды. Поверхность пирамиды
Пирамида. Элементы пирамиды. Поверхность пирамиды Решение задач на разностное сравнение 2 класс - Презентация
Решение задач на разностное сравнение 2 класс - Презентация Методы мотивации и стимулирования деятельности обучающихся на уроках математики
Методы мотивации и стимулирования деятельности обучающихся на уроках математики Устный счет на уроке геометрии в 8 классе
Устный счет на уроке геометрии в 8 классе