Параллельность прямых и плоскостей в пространстве

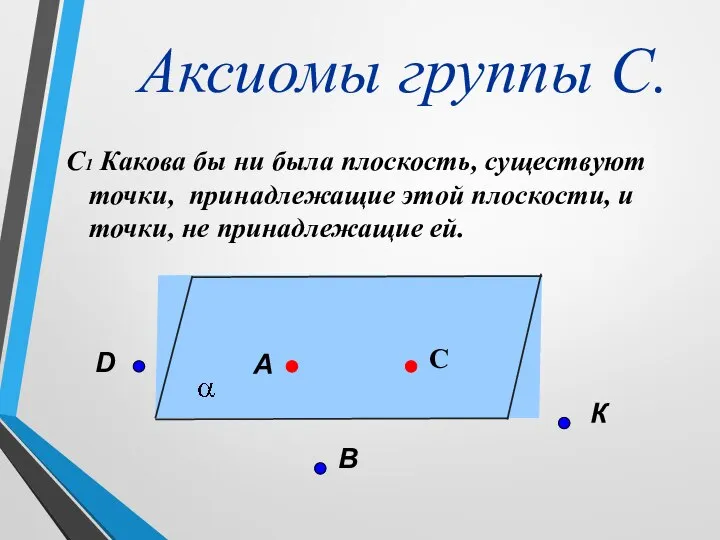
Аксиомы группы С.
С1 Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
А
К
D
B
С

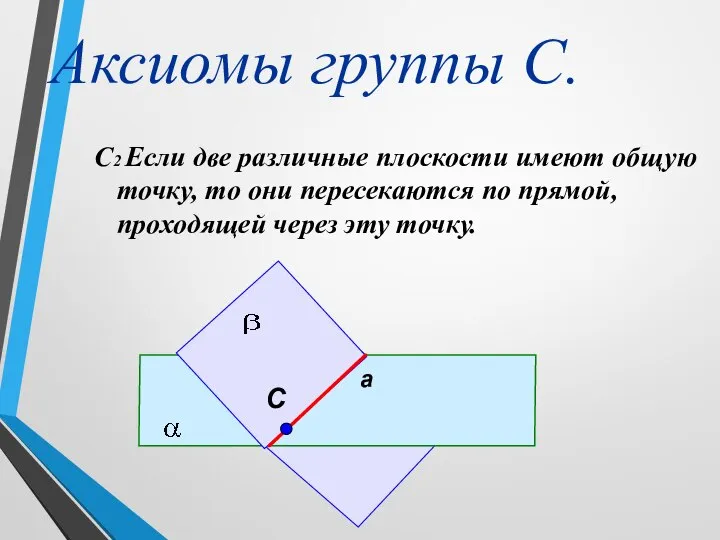
Аксиомы группы С.
С2 Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
С
а

Аксиомы группы С.
С3 Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
a
b
С

Через любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну.
α
М
Следствия из аксиом
Т

Если две точки прямой принадлежат плоскости, то вся прямая принадлежит плоскости
α
А
В
Следствия из аксиом
Т

Через 3 точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
α
М
А
В
Следствия из аксиом
Т

Взаимное расположение прямых в пространстве.

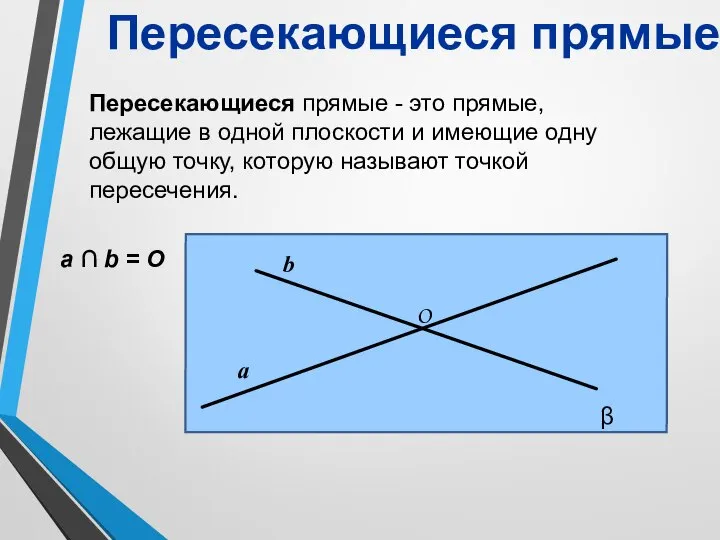
а
b
Пересекающиеся прямые
Пересекающиеся прямые - это прямые, лежащие в одной плоскости и имеющие одну общую точку, которую называют точкой пересечения.
а ∩ b = O
O
β

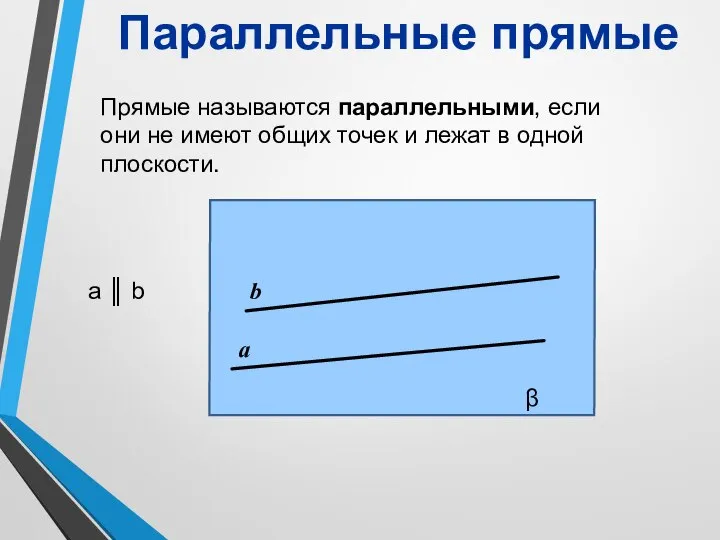
а
b
Параллельные прямые
Прямые называются параллельными, если они не имеют общих точек и лежат в одной плоскости.
a ║ b
β

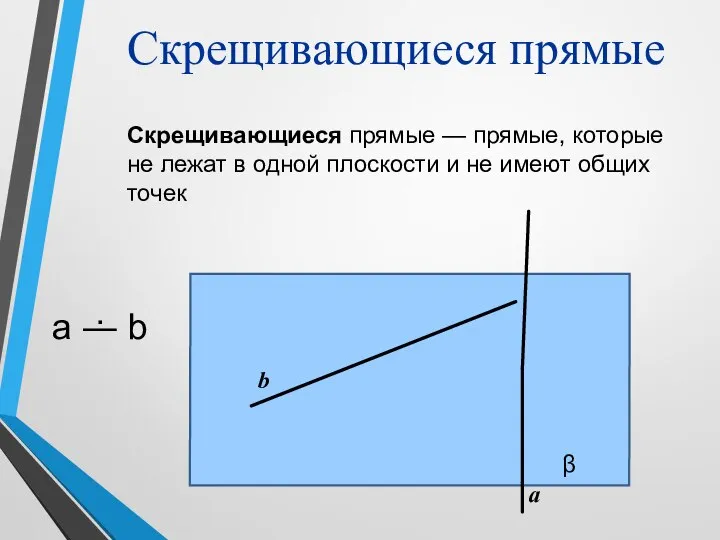
а
b
Скрещивающиеся прямые
Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости и не имеют общих точек
β
a ― b
.

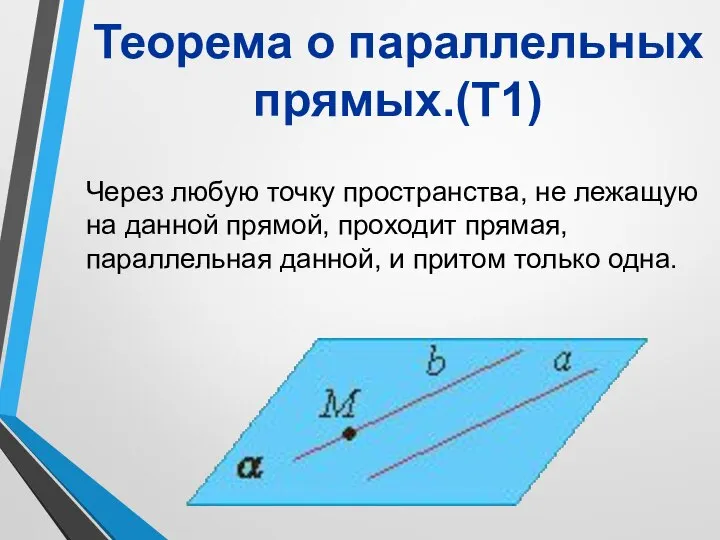
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Теорема о параллельных прямых.(Т1)

Две прямые, параллельные третьей прямой, параллельны друг другу.
Признак параллельности прямых
С
Если: a ║ c и b ║ c, то а ║ b

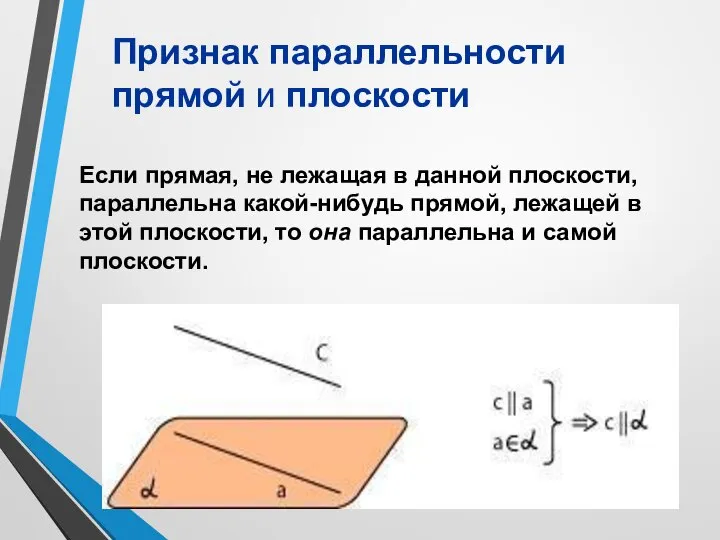
Если прямая, не лежащая в данной плоскости,
параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна и самой плоскости.
Признак параллельности прямой и плоскости

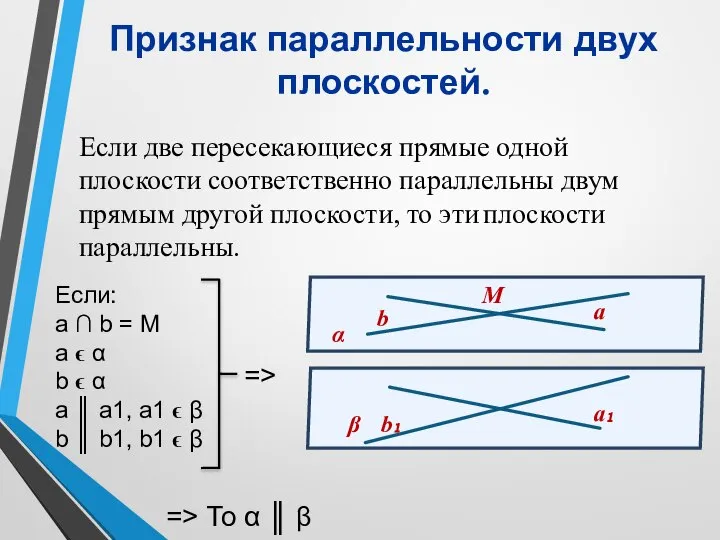
Признак параллельности двух плоскостей.
Если две пересекающиеся прямые одной
плоскости соответственно параллельны двум
прямым другой плоскости, то эти плоскости параллельны.
β
α
а
а₁
b
b₁
M
Если:
a ∩ b = M
a ϵ α
b ϵ α
a ║ a1, a1 ϵ β
b ║ b1, b1 ϵ β
=>
=> То α ║ β