Содержание
- 2. где s – исправленное выборочное среднее квадратическое отклонение, а для δ выполняется условие: или
- 3. Обозначив (1) Рассмотрим случайную величину Х, определяемую по формуле
- 4. Плотность распределения С имеет вид: Это распределение не зависит от оцениваемого параметра s, а зависит только
- 5. q , тогда получаем: или
- 6. Пример 1. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n=25 найдено исправленное среднее
- 7. Решение 1. Используя заданные значения , по таблице находим значение q=0.32. Искомый доверительный интервал есть: Необходимо
- 8. Пример 2. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n=10 найдено «исправленное» среднее
- 9. Решение 2. По таблице по данным = 0,999 и n =10 найдем q = l,8 (q
- 11. Скачать презентацию








 Наибольшие и найменьшее значение функции
Наибольшие и найменьшее значение функции Кубический корень
Кубический корень Основные характеристики средств измерений. Лекция 4
Основные характеристики средств измерений. Лекция 4 Логарифмическая функция. Тест
Логарифмическая функция. Тест Уравнение плоскости
Уравнение плоскости Цели урока:
Цели урока: Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Простейшие уравнения
Простейшие уравнения Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Геологические приложения одномерной статистической модели
Геологические приложения одномерной статистической модели Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся
Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся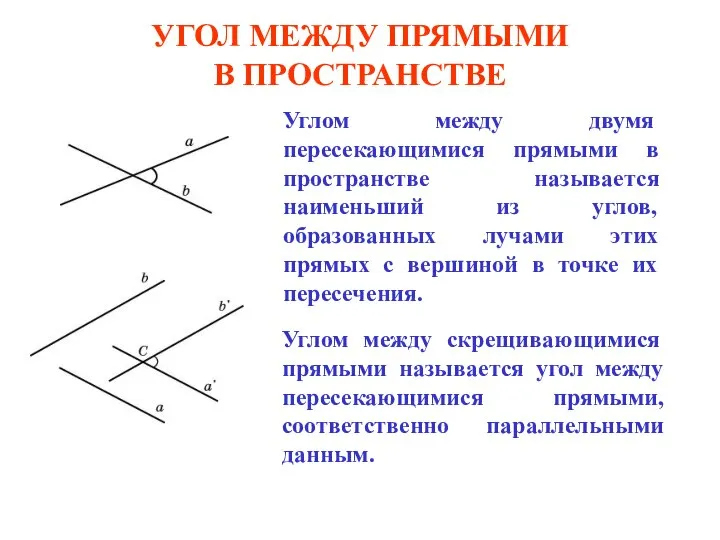 Угол между двумя прямыми в пространстве Вариант 2.ppt
Угол между двумя прямыми в пространстве Вариант 2.ppt Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс
Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс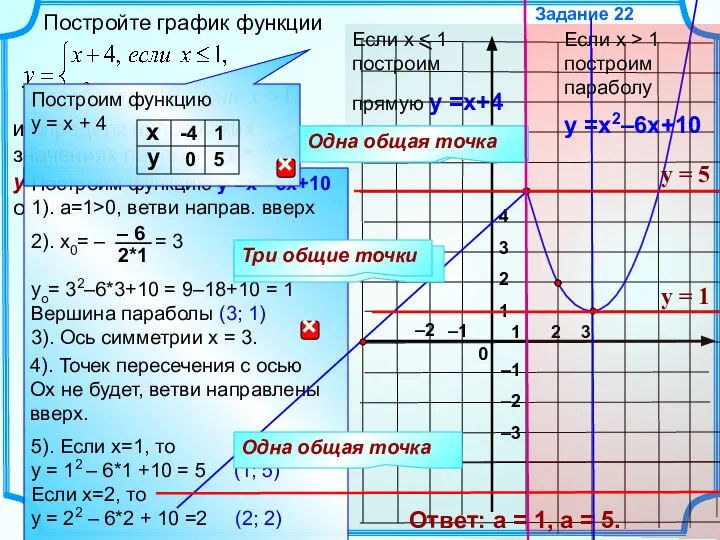 Парабола прямая. Часть II
Парабола прямая. Часть II Второй признак подобия треугольников
Второй признак подобия треугольников Степень с натуральным показателем. Обобщающий урок в 7 классе
Степень с натуральным показателем. Обобщающий урок в 7 классе Решение задач
Решение задач Пирамида
Пирамида Презентация на тему Решение неравенств методом интервалов (9 класс)
Презентация на тему Решение неравенств методом интервалов (9 класс)  Упрощение выражений. Тест
Упрощение выражений. Тест Сумма углов треугольника
Сумма углов треугольника Вычисление производной и правила дифференцирования
Вычисление производной и правила дифференцирования Умножение и деление смешанных дробей
Умножение и деление смешанных дробей Математическая тревожность
Математическая тревожность Решение логарифмических уравнений
Решение логарифмических уравнений Решение систем неравенств
Решение систем неравенств Семь чудес Кузбасса 5 класс
Семь чудес Кузбасса 5 класс Признаки равенства треугольников
Признаки равенства треугольников