Содержание
- 2. Эквивалентные преобразования умножение строки на ненулевое число перестановка двух строк прибавление к одной строке матрицы другой
- 3. употребляется знаки: ~; ⇔ ; ↔
- 4. Рассмотрим пример эквивалентных преобразований Пусть задана матраца А = 3 3 3 2 2 2 х
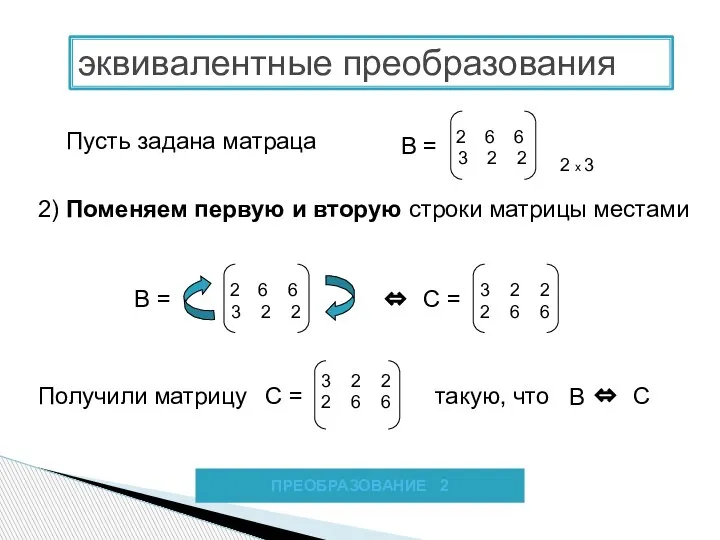
- 5. 2) Поменяем первую и вторую строки матрицы местами Пусть задана матраца В = 6 6 3
- 6. Пусть задана матраца С = 3 2 2 2 6 6 3) От первой строки матрицы
- 7. Пусть задана матраца D = 1 -4 -4 2 6 6 2 х 3 4) Проведём
- 9. Определение: Ранг матрицы равен числу ненулевых строк матрицы, приведенной к треугольному виду. Обозначают rang(A) или r(A)
- 11. Метод элементарных преобразований Задание. Найти ранг матрицы 0 4 10 1 4 8 18 4 18
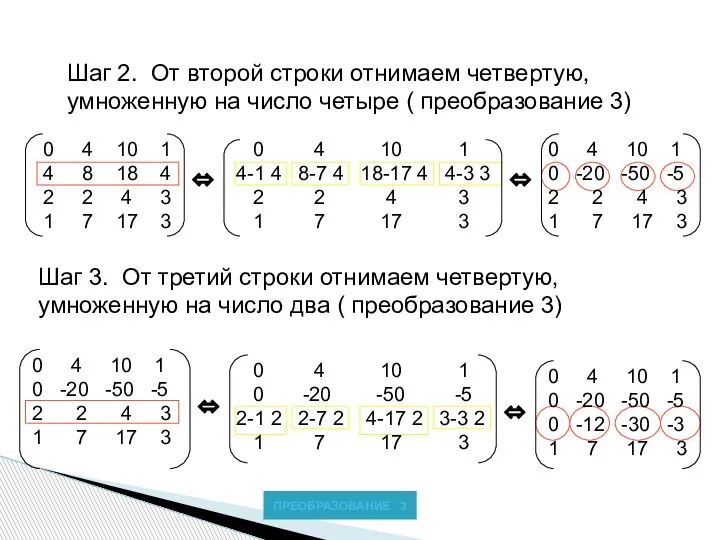
- 12. Шаг 2. От второй строки отнимаем четвертую, умноженную на число четыре ( преобразование 3) 0 4
- 13. Шаг 4. К второй строки прибавим первую, умноженную на число пять ( преобразование 3) ⇔ 0
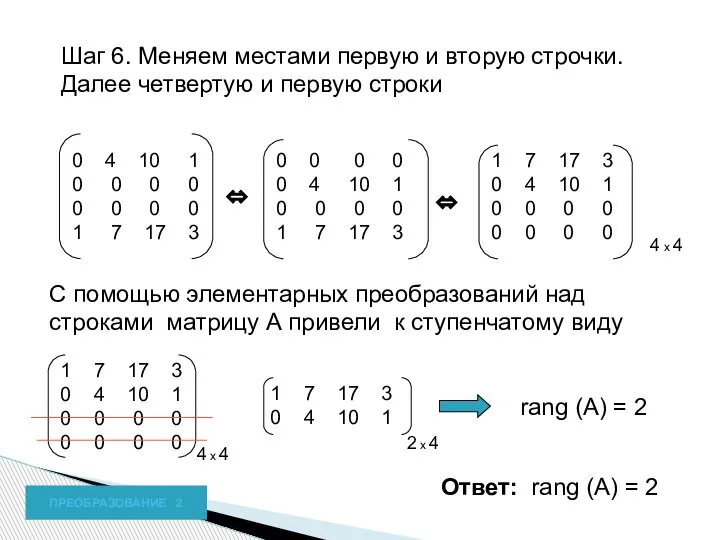
- 14. Шаг 6. Меняем местами первую и вторую строчки. Далее четвертую и первую строки ПРЕОБРАЗОВАНИЕ 2 0
- 16. Скачать презентацию










 Площадь. Фигуры
Площадь. Фигуры Векторное кодирование графической информации. Практическая работа. 6 класс
Векторное кодирование графической информации. Практическая работа. 6 класс Простейшие задачи в координатах
Простейшие задачи в координатах Контрольная работа №8 по теме Разложение многочленов на множители
Контрольная работа №8 по теме Разложение многочленов на множители Использование занимательных игровых упражнений при обучении элементарной математики для развития логического мышления дошкольн
Использование занимательных игровых упражнений при обучении элементарной математики для развития логического мышления дошкольн Граф – набор точек, некоторые из которых соединены линиями
Граф – набор точек, некоторые из которых соединены линиями Презентация на тему Решение неравенств методом интервалов
Презентация на тему Решение неравенств методом интервалов  Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис
Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис Математические ребусы. 4 класс
Математические ребусы. 4 класс Презентация на тему Объём шара и его частей
Презентация на тему Объём шара и его частей  Метод деформируемого многогранника (Нелдера-Мида)
Метод деформируемого многогранника (Нелдера-Мида) Таблица умножения на 2
Таблица умножения на 2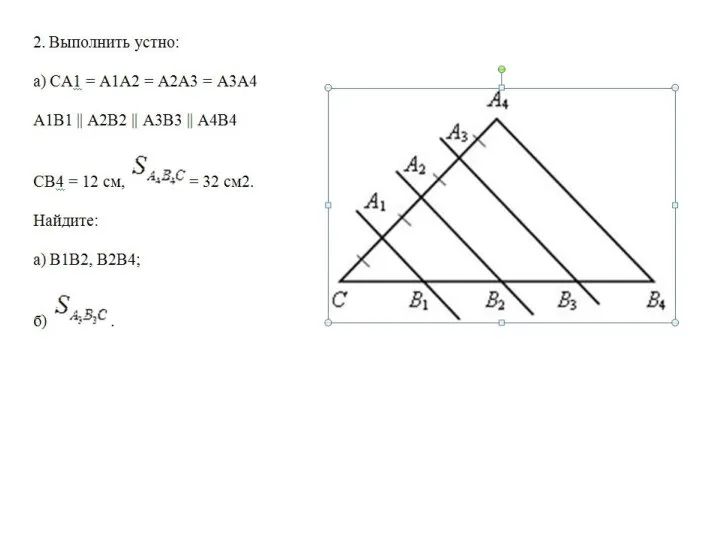 Признаки подобия треугольников. Урок 31
Признаки подобия треугольников. Урок 31 Технология подготовки учащихся к овладению функционально-графическими методами решения задач с параметрами. (Занятие №3)
Технология подготовки учащихся к овладению функционально-графическими методами решения задач с параметрами. (Занятие №3) Комплексные числа
Комплексные числа По какому принципу образован ряд
По какому принципу образован ряд Системы линейных уравнений с двумя переменными
Системы линейных уравнений с двумя переменными Решение треугольников
Решение треугольников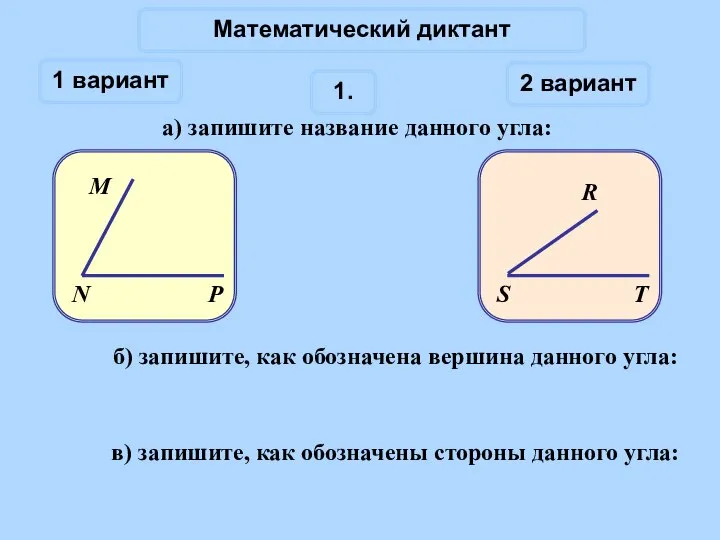 Углы. Математический диктант
Углы. Математический диктант Теория вероятностей
Теория вероятностей Задача № 106
Задача № 106 Презентация на тему Занимательная математика
Презентация на тему Занимательная математика  Степень с натуральным показателем и его свойства
Степень с натуральным показателем и его свойства Площа фігури. Задачі на спільну роботу
Площа фігури. Задачі на спільну роботу Методы кластеризации
Методы кластеризации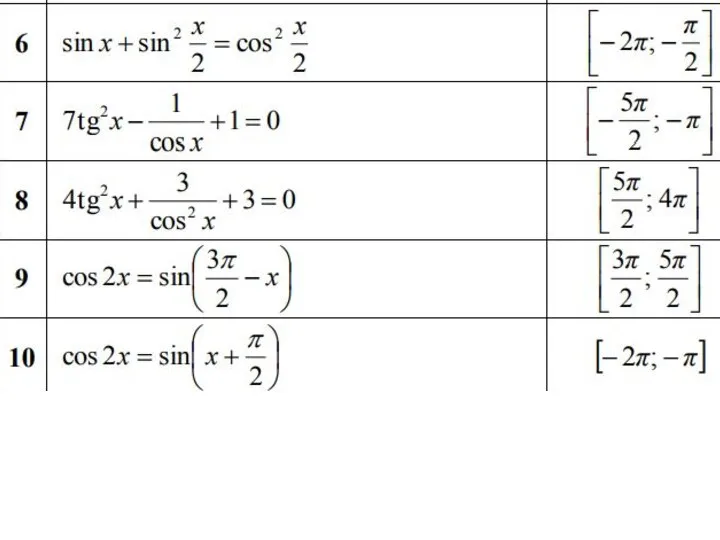 Решение уравнений
Решение уравнений Тренажёр. Единицы измерения
Тренажёр. Единицы измерения Математическая статистика. Лекция 2
Математическая статистика. Лекция 2