ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.
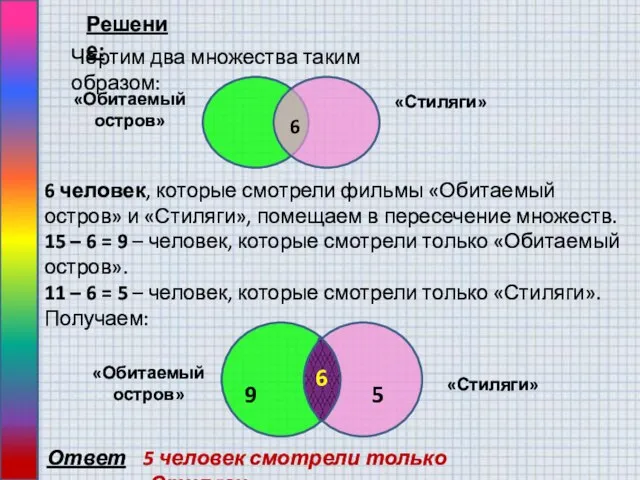
Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят.
Сноуборд
Ответ.
20 человек не умеют кататься ни на одном спортивном снаряде.

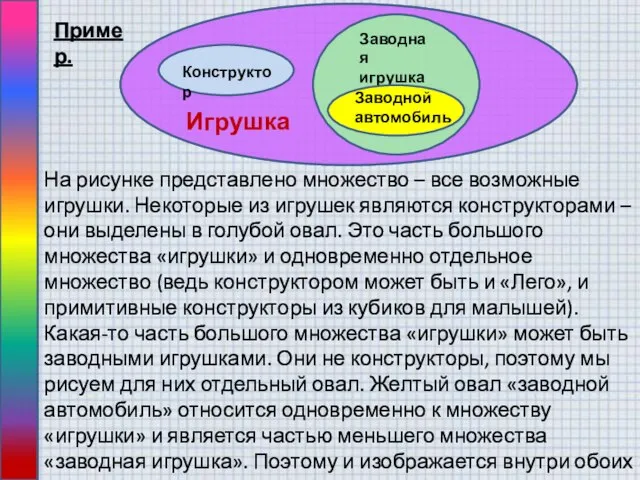




 Презентация на тему Теорема Виета
Презентация на тему Теорема Виета 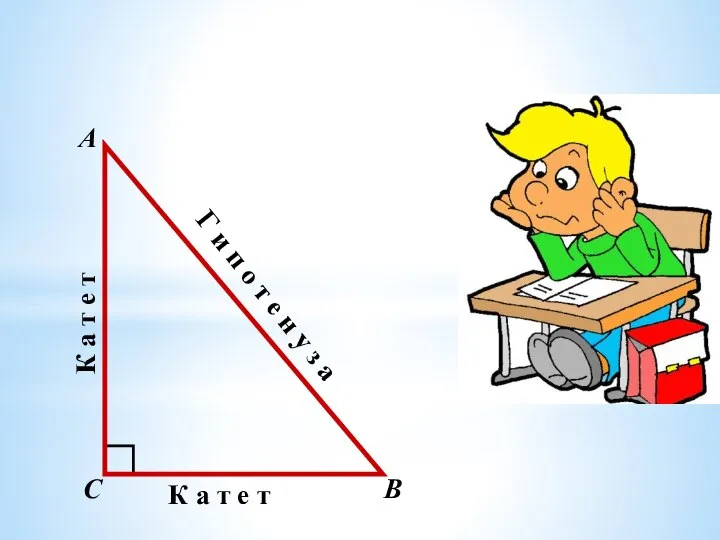 Гипотенуза и катеты в треугольнике. Задачи
Гипотенуза и катеты в треугольнике. Задачи Математика. Проверочная работа
Математика. Проверочная работа Графическое решение задач
Графическое решение задач Ответы к тестам для подготовки к ЕГЭ по математике
Ответы к тестам для подготовки к ЕГЭ по математике Преобразование в плоскости. Методика изучения симметрии в начальной школе
Преобразование в плоскости. Методика изучения симметрии в начальной школе Стереометрия. Основные фигуры в пространстве
Стереометрия. Основные фигуры в пространстве Простые и составные числа
Простые и составные числа Решение иррациональных уравнений
Решение иррациональных уравнений Цифра 8
Цифра 8 Игра Жизнь Conway's Game of Life
Игра Жизнь Conway's Game of Life Математическая викторина
Математическая викторина Решение систем уравнений
Решение систем уравнений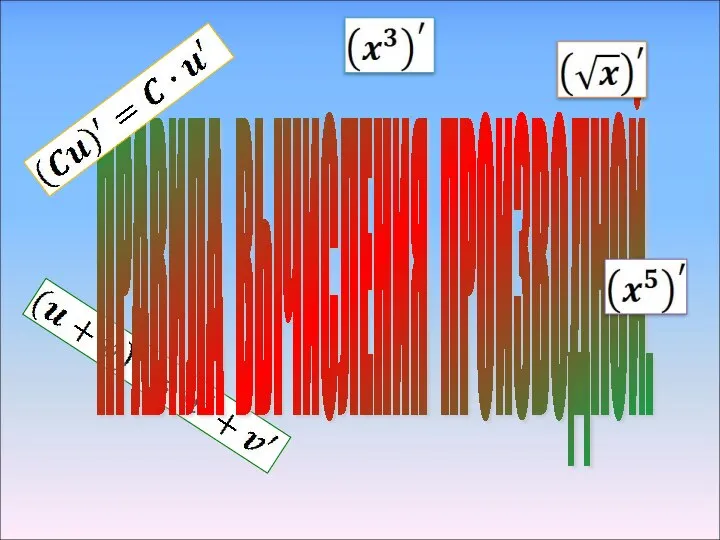 Правила вычисления производной
Правила вычисления производной Предсказание будущего
Предсказание будущего Пирамида. Усеченная пирамида
Пирамида. Усеченная пирамида Сумма углов треугольника
Сумма углов треугольника Расстояние между точками
Расстояние между точками Урок математики в 10 классе по теме Пирамида
Урок математики в 10 классе по теме Пирамида Сумма углов треугольника
Сумма углов треугольника Задания для домашнего обучения
Задания для домашнего обучения Интерполирование полиномами Ньютона
Интерполирование полиномами Ньютона Таблица сложения
Таблица сложения Просто, сложно, интересно. Учебный курс предпрофильной подготовки для учащихся 9-х классов
Просто, сложно, интересно. Учебный курс предпрофильной подготовки для учащихся 9-х классов Обыкновенные дроби. Основное свойство дроби. 5 класс
Обыкновенные дроби. Основное свойство дроби. 5 класс Двоичная арифметика
Двоичная арифметика Золотое сечение и гармония форм природы и искусства. 8 класс
Золотое сечение и гармония форм природы и искусства. 8 класс Презентация по математике "Дроби на Руси" -
Презентация по математике "Дроби на Руси" -