Комбинаторика

ЧТО ТАКОЕ КОМБИНАТОРИКА?
Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Слово «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять».
Термин "комбинаторика" был введён знаменитым Готфридом Вильгельмом Лейбницем, - всемирно известным немецким учёным.

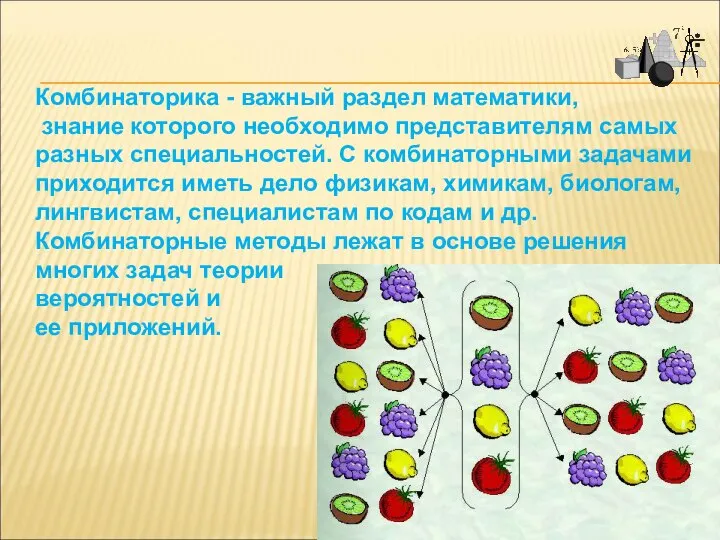
Комбинаторика - важный раздел математики,
знание которого необходимо представителям самых разных специальностей. С комбинаторными задачами приходится иметь дело физикам, химикам, биологам, лингвистам, специалистам по кодам и др.
Комбинаторные методы лежат в основе решения многих задач теории
вероятностей и
ее приложений.

В Древней Греции
подсчитывали число различных комбинаций длинных и коротких слогов в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые можно составить из частей и т.д.
Со временем появились различные игры
(нарды, карты, шашки, шахматы и т. д.)
В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучал, знал выигрышные комбинации и умел избегать проигрышных.

Готфрид Вильгельм Лейбниц
(1.07.1646 - 14.11.1716)
Комбинаторику, как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666г. Он также впервые ввел термин «Комбинаторика».
Леонард Эйлер(1707-1783)
рассматривал задачи о разбиении чисел, о паросочетаниях, циклических расстановках, о построении магических и латинских квадратов, положил начало совершенно новой области исследований, выросшей впоследствии в большую и важную науку—топологию, которая изучает общие свойства пространства и фигур.

ПРАВИЛО СУММЫ
Если некоторый объект A можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить (m+n) способами.
При использовании правила суммы надо следить, чтобы ни один из способов выбора объекта А не совпадал с каким-либо способом выбора объекта В.
Если такие совпадения есть, правило суммы утрачивает силу, и мы получаем лишь (m + n - k) способов выбора, где k—число совпадений.

РЕШЕНИЕ ЗАДАЧ
В коробке находится 10 шаров: 3 белых, 2 черных, 1 синий и 4 красных. Сколькими способами можно взять из ящика цветной шар?
Решение:
Цветной шар – это синий или красный, поэтому применим правило суммы:
+
=

ПРАВИЛО ПРОИЗВЕДЕНИЯ
Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары (А,В) в указанном порядке можно осуществить mn способами.
При этом число способов выбора второго элемента не зависит от того, как именно выбран первый элемент.

РЕШЕНИЕ ЗАДАЧ
Сколько может быть различных комбинаций выпавших
граней при бросании двух игральных костей?
Решение:
На первой кости может быть: 1,2,3,4,5 и 6 очков, т.е. 6 вариантов.
На второй – 6 вариантов.
Всего: 6*6=36 вариантов.
Правила суммы и произведения верны для любого количества объектов.

ВЫБЕРИТЕ ПРАВИЛО
№1. Из города А а город В ведут 6 дорог, а из города В в город С – 3 дороги. Сколькими способами можно проехать из города А в город С?
№2. На книжной полке стоят 3 книги по алгебре, 7 по геометрии и 2 по литературе. Сколькими способами можно взять с полки одну книгу по математике?
№3. В меню имеется 4 первых блюда, 3 – вторых, 2 – десерта. Сколько различных обедов можно из них составить?

« Эн факториал»-n!.
Определение.
Произведение подряд идущих первых n
натуральных чисел обозначают n! и называют
«эн факториал»: n!=1•2•3•…•(n-1)•n.
2!=
1•2=
2
3!=
1•2•3=
6
4!=
1•2•3•4=
24
5!=
1•2•3•4•5=
6!=
120
1•2•3•4•5•6=
720
7!=
1•2•3•4•5•6•7=
5040
n!=(n-1)!•n
Удобная формула!!!

Комбинации из n-элементов, отличающиеся друг от друга только порядком следования элементов, называются перестановками.
Обозначаются Рn
Перестановки

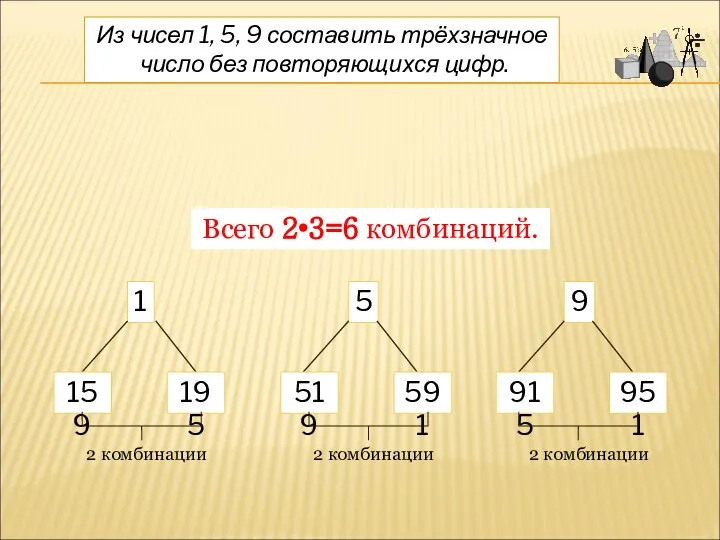
Из чисел 1, 5, 9 составить трёхзначное
число без повторяющихся цифр.
1
159
195
5
9
519
591
915
951
2 комбинации
2 комбинации
2 комбинации
Всего 2•3=6 комбинаций.

Комбинации из n-элементов по k, отличающиеся друг от друга составом и порядком, называются размещениями.
Размещения

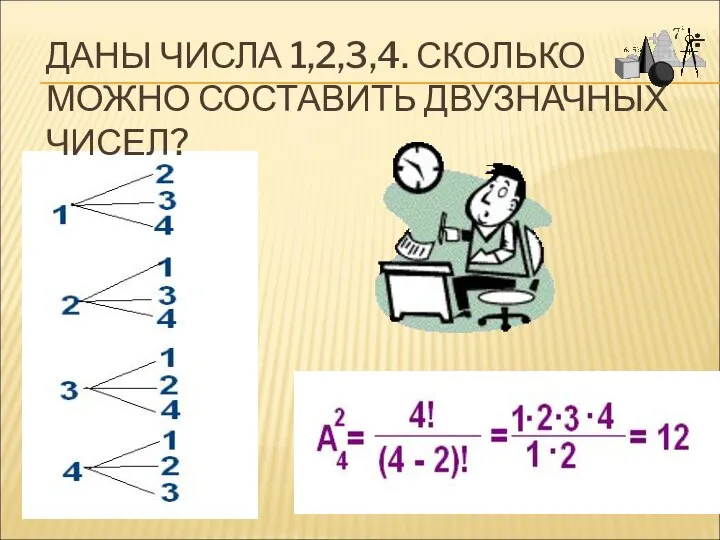
ДАНЫ ЧИСЛА 1,2,3,4. СКОЛЬКО МОЖНО СОСТАВИТЬ ДВУЗНАЧНЫХ ЧИСЕЛ?

Комбинации из n-элементов по к, отличающиеся только составом элементов, называются сочетаниями из n -элементов по к.
Сочетания

РЕШЕНИЕ ЗАДАЧ
Из 20 учащихся надо выбрать двух дежурных.
Сколькими способами это можно сделать?
Решение:
Надо выбрать двух человек из 20.
Ясно, что от порядка выбора ничего не зависит, то есть
Иванов - Петров или Петров - Иванов - это одна
и та же пара дежурных. Следовательно, это будут сочетания из 20 по 2.