Содержание
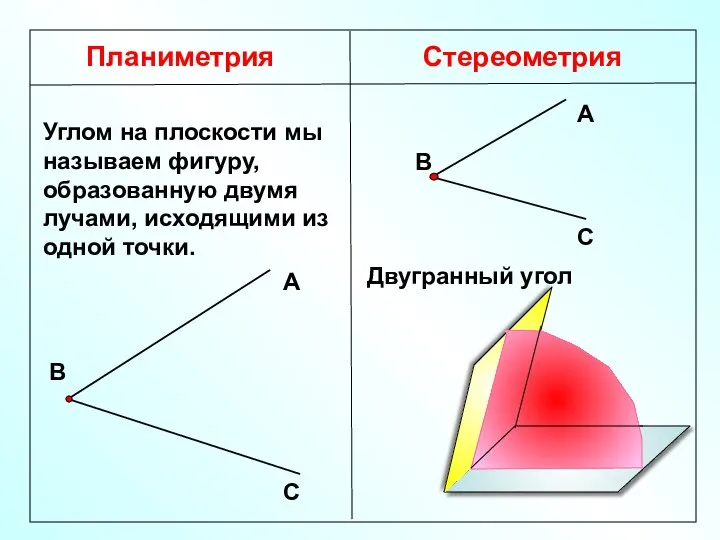
- 2. Планиметрия Стереометрия Углом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из одной точки. Двугранный
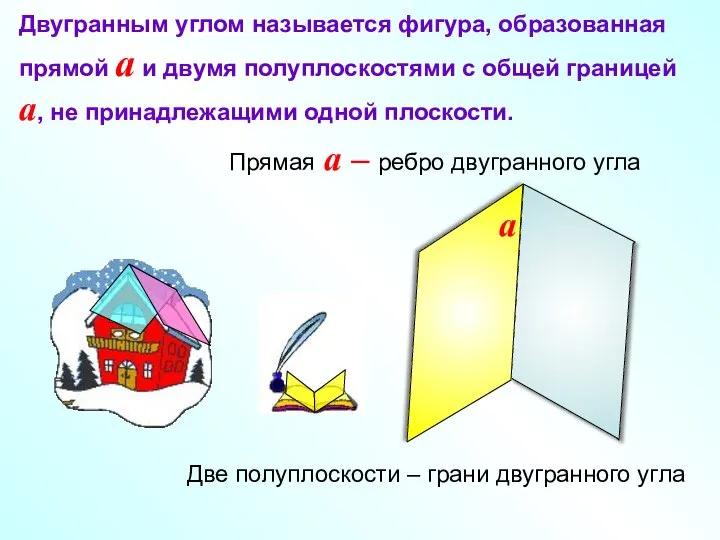
- 3. Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими
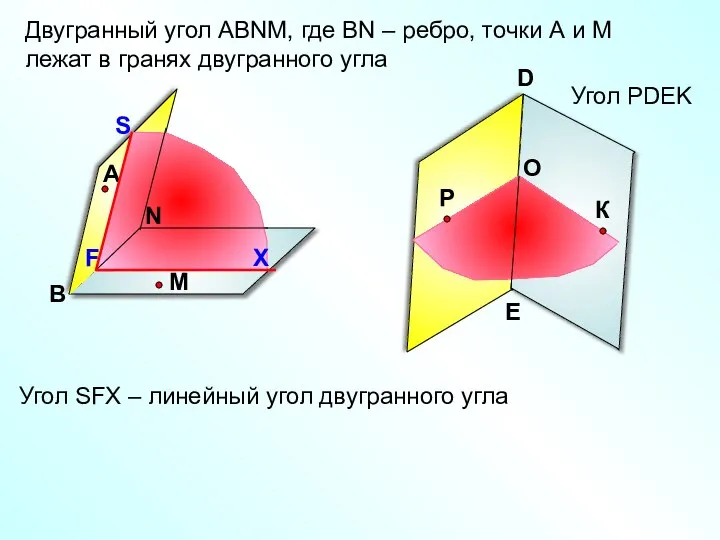
- 4. Угол РDEK Двугранный угол АВNМ, где ВN – ребро, точки А и М лежат в гранях
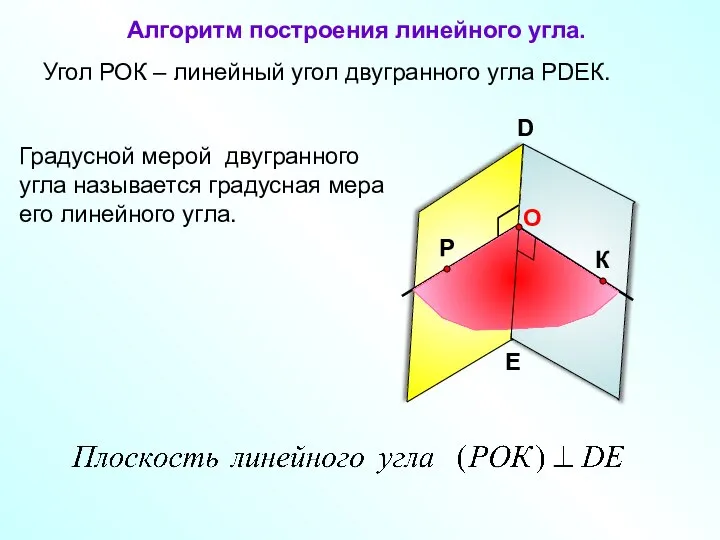
- 5. Угол РОК – линейный угол двугранного угла РDEК. D E Градусной мерой двугранного угла называется градусная
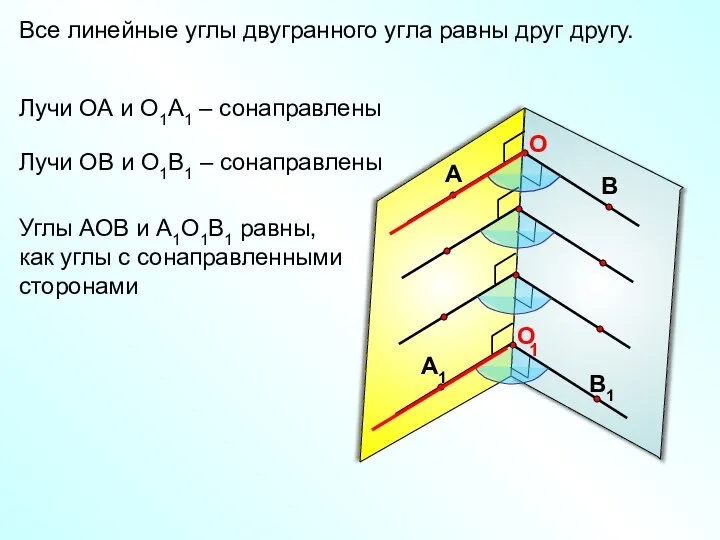
- 6. Все линейные углы двугранного угла равны друг другу. 1 Лучи ОА и О1А1 – сонаправлены Лучи
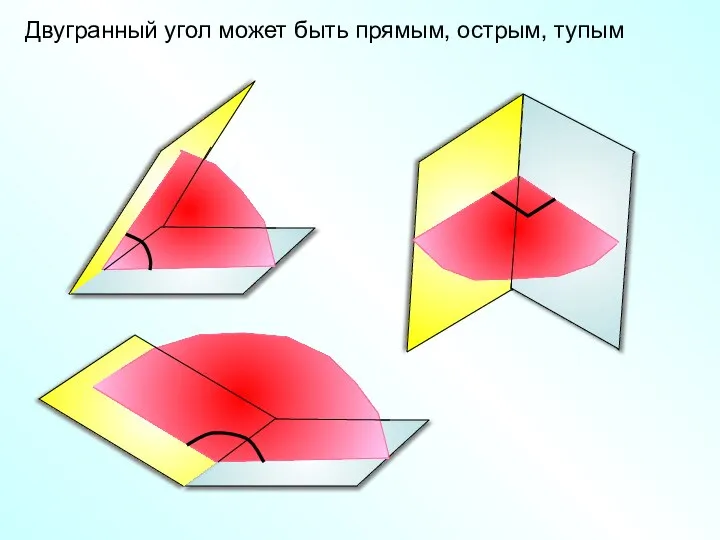
- 7. Двугранный угол может быть прямым, острым, тупым
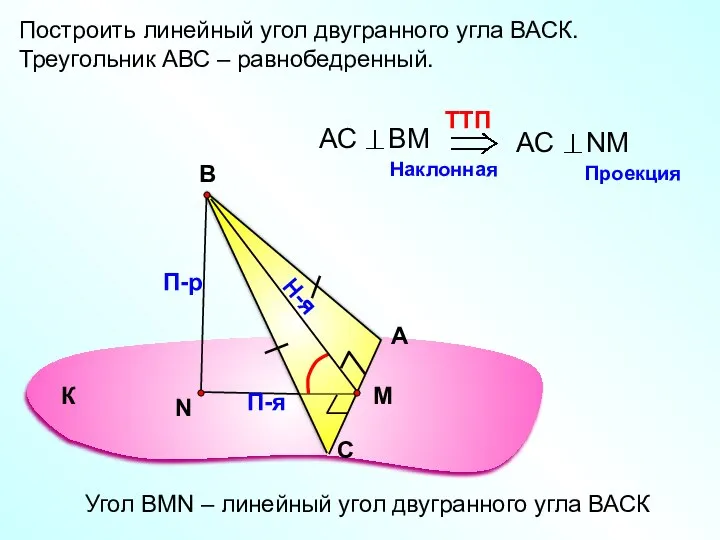
- 8. Построить линейный угол двугранного угла ВАСК. Треугольник АВС – равнобедренный. А С В П-р Н-я П-я
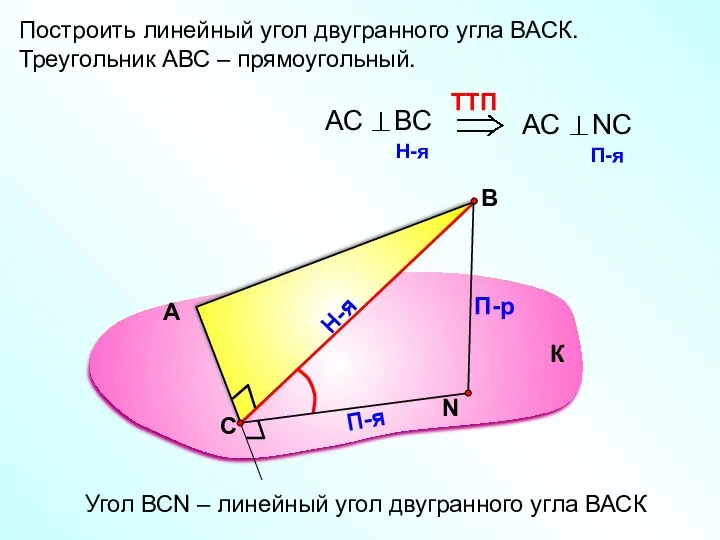
- 9. Построить линейный угол двугранного угла ВАСК. Треугольник АВС – прямоугольный. А В П-р Н-я П-я Угол
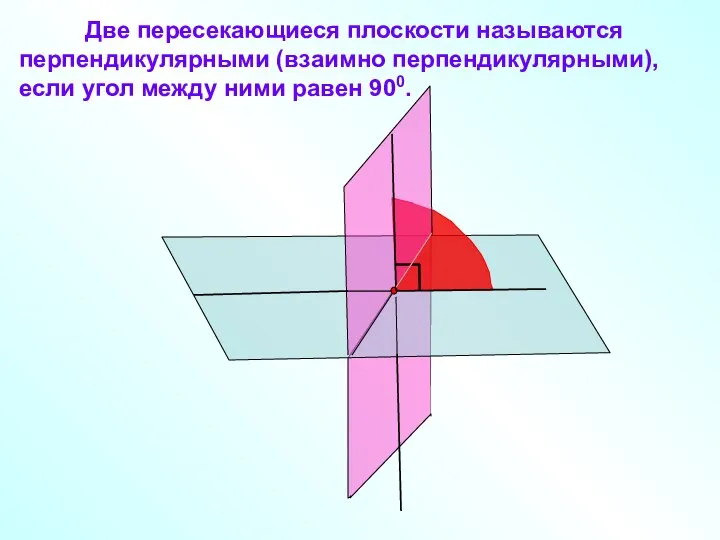
- 10. Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 900.
- 11. Примером взаимно перпендикулярных плоскостей служат плоскости стены и пола комнаты, плоскости стены и потолка.
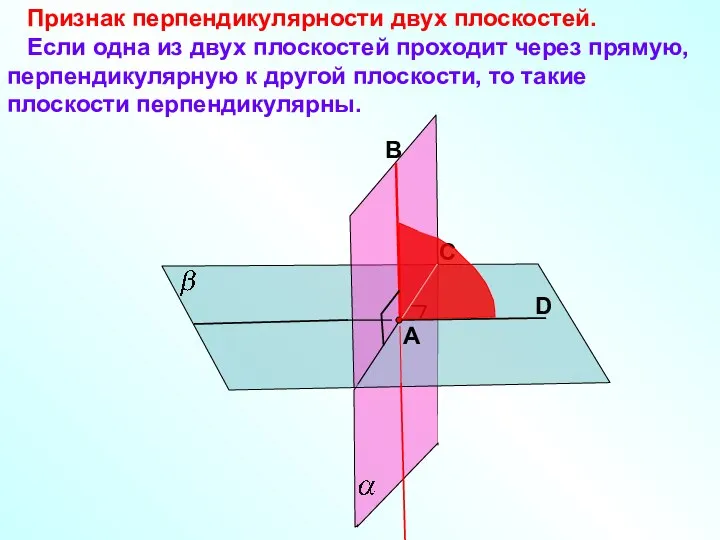
- 12. Признак перпендикулярности двух плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости,
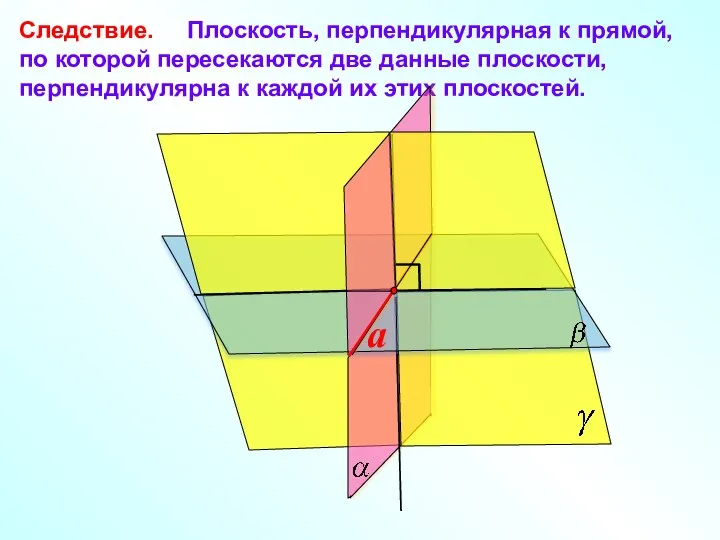
- 13. Следствие. Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой их этих
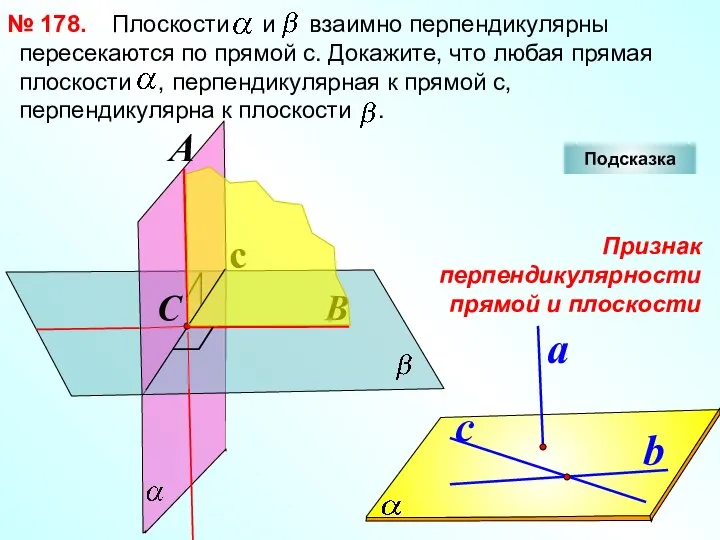
- 14. Плоскости и взаимно перпендикулярны пересекаются по прямой с. Докажите, что любая прямая плоскости , перпендикулярная к
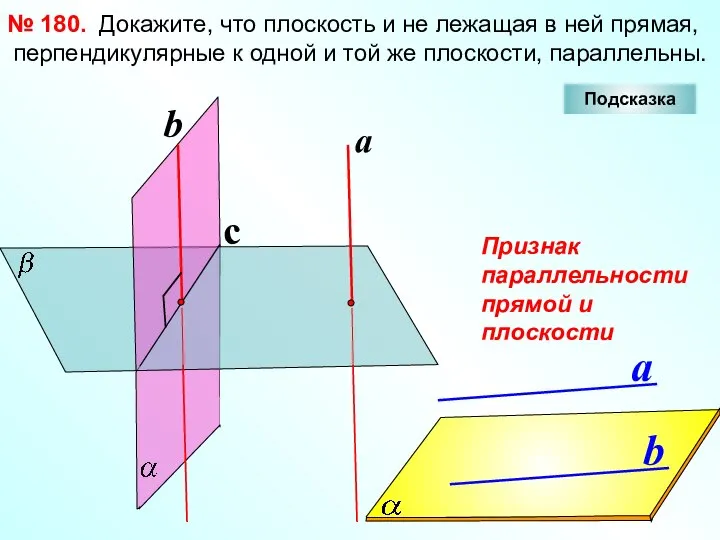
- 15. Докажите, что плоскость и не лежащая в ней прямая, перпендикулярные к одной и той же плоскости,
- 16. № 181. С М a
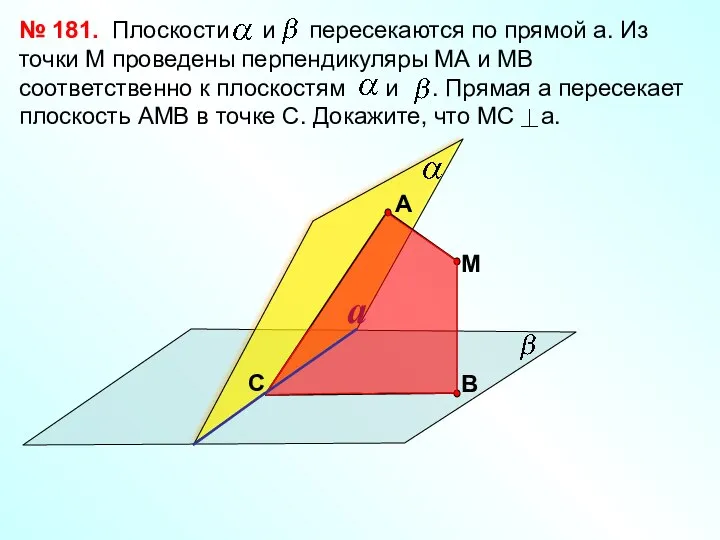
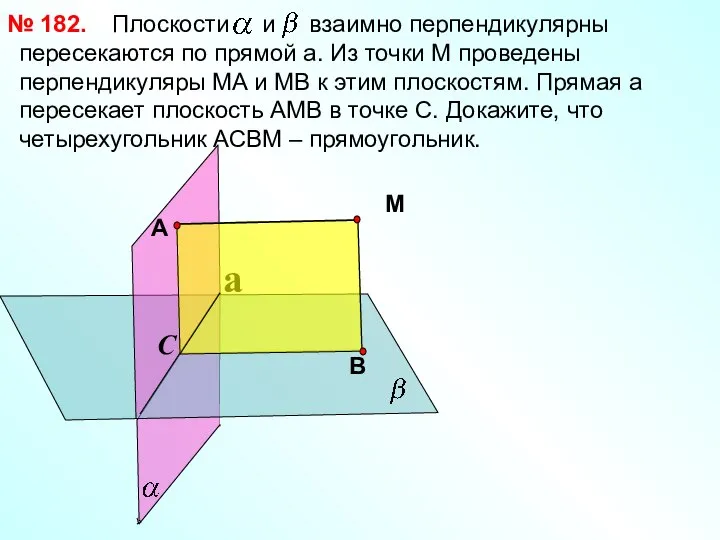
- 17. Плоскости и взаимно перпендикулярны пересекаются по прямой a. Из точки М проведены перпендикуляры МА и МВ
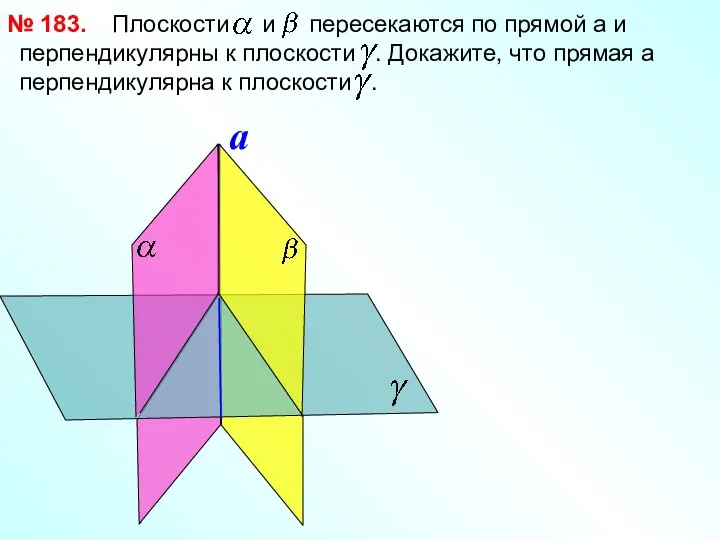
- 18. Плоскости и пересекаются по прямой a и перпендикулярны к плоскости . Докажите, что прямая а перпендикулярна
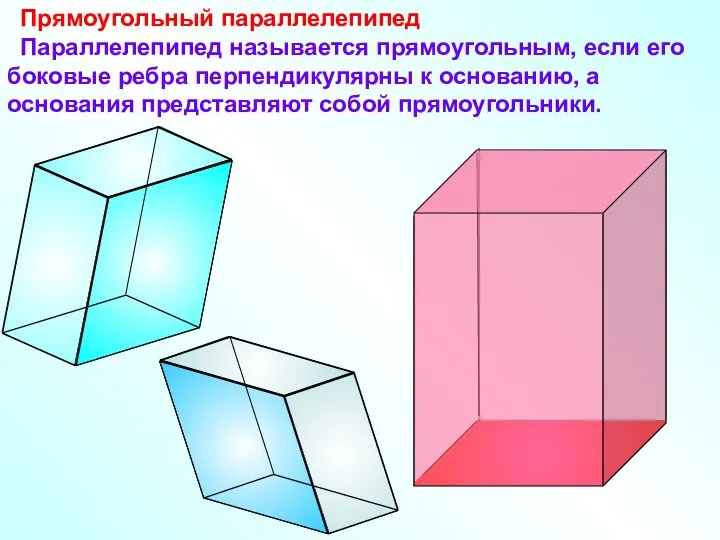
- 19. Прямоугольный параллелепипед Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой
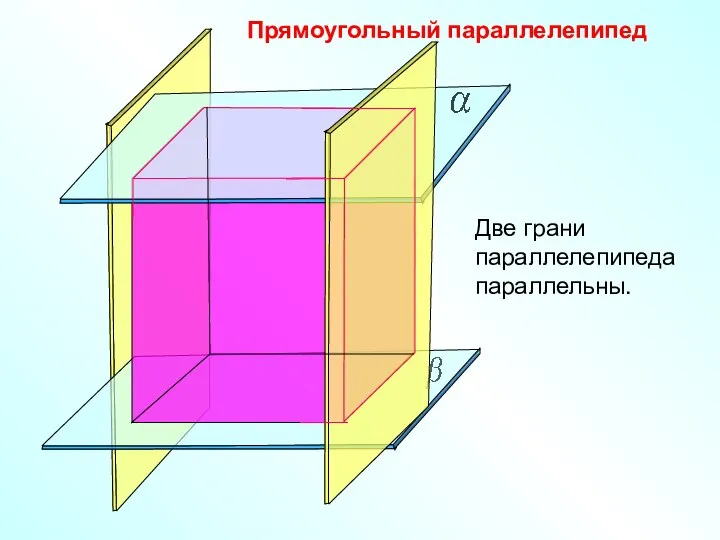
- 20. Прямоугольный параллелепипед Две грани параллелепипеда параллельны.
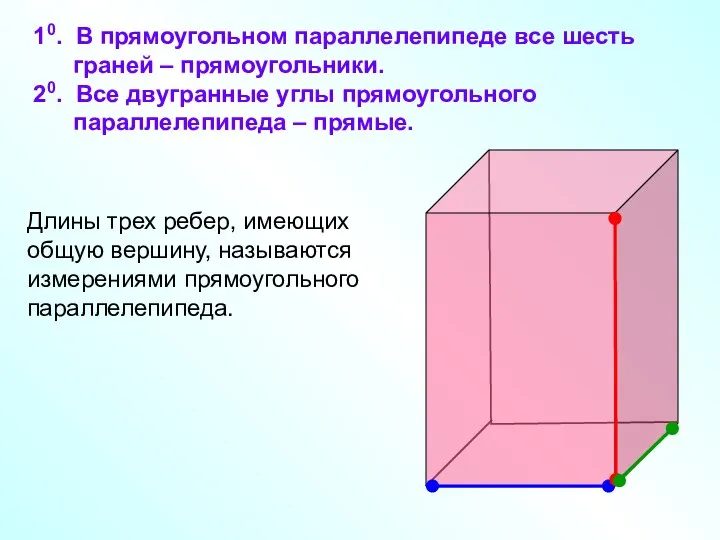
- 21. 10. В прямоугольном параллелепипеде все шесть граней – прямоугольники. 20. Все двугранные углы прямоугольного параллелепипеда –
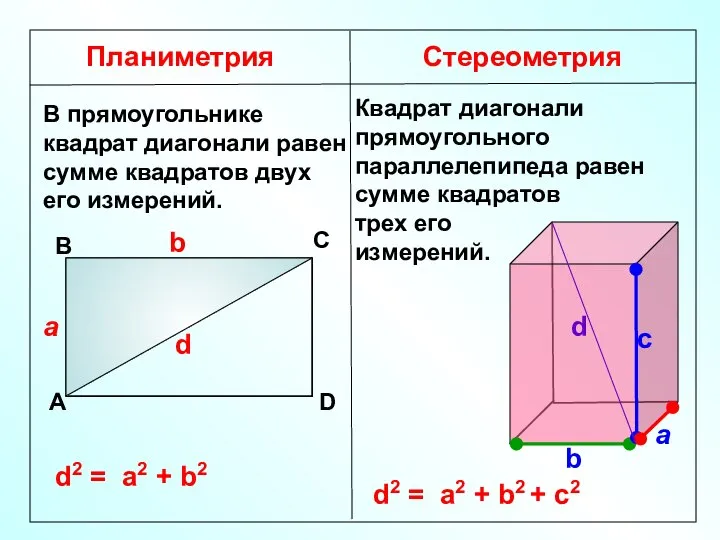
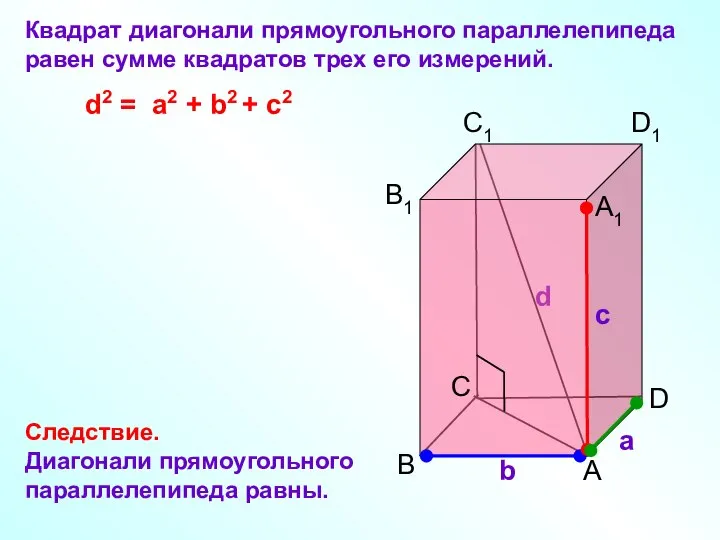
- 22. Планиметрия Стереометрия В прямоугольнике квадрат диагонали равен сумме квадратов двух его измерений. А В С D
- 23. C а b с B A D B1 C1 D1 A1 Квадрат диагонали прямоугольного параллелепипеда равен
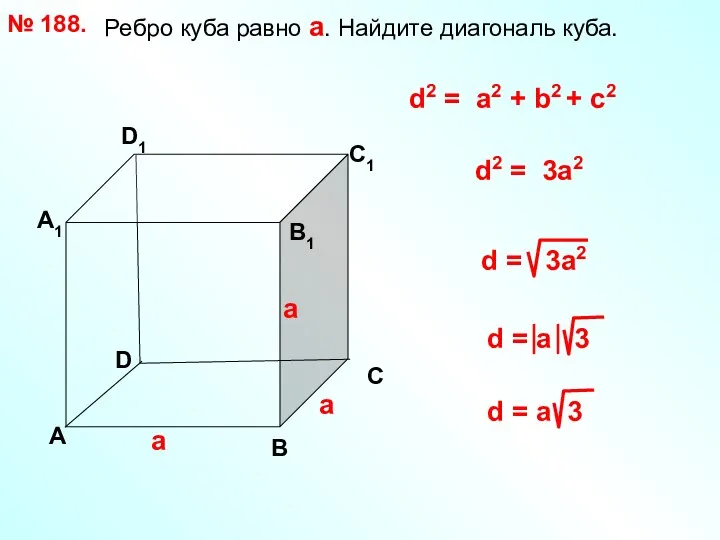
- 24. Ребро куба равно а. Найдите диагональ куба. № 188. D А В С А1 D1 С1
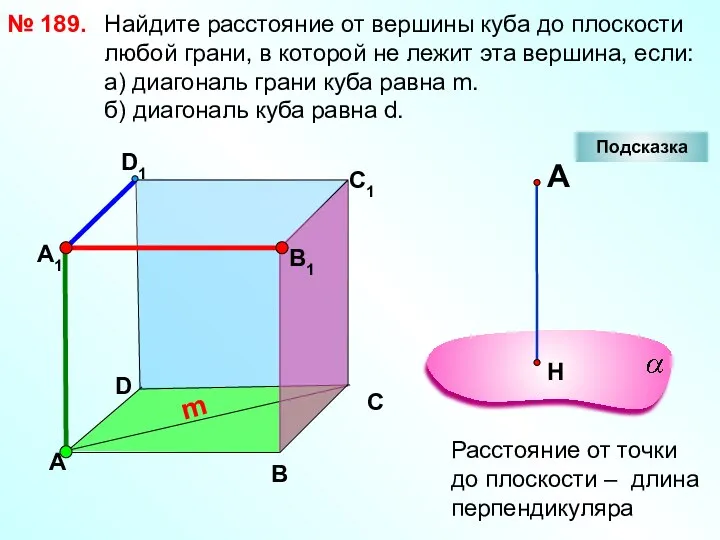
- 25. Найдите расстояние от вершины куба до плоскости любой грани, в которой не лежит эта вершина, если:
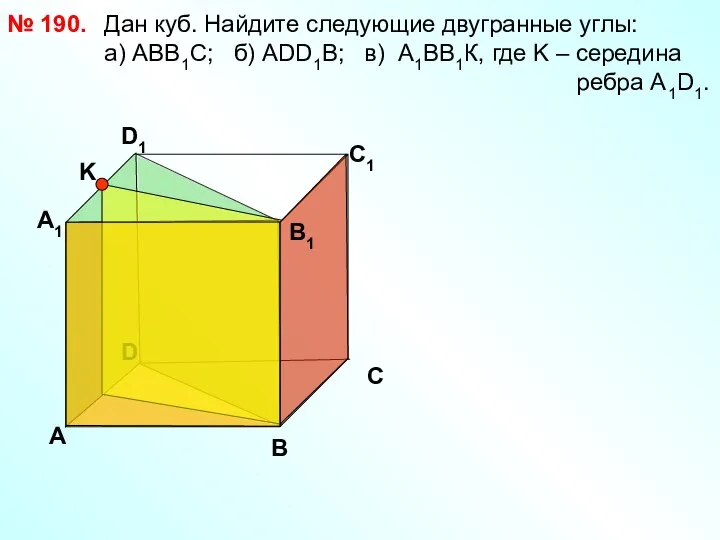
- 26. Дан куб. Найдите следующие двугранные углы: a) АВВ1С; б) АDD1B; в) А1ВВ1К, где K – середина
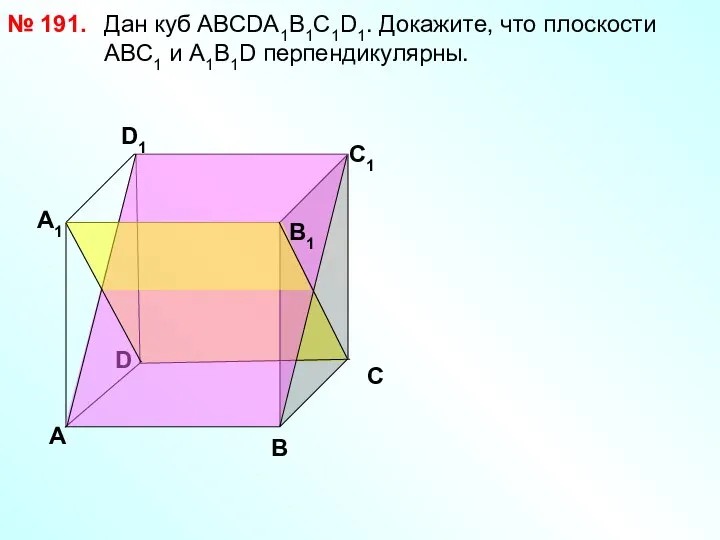
- 27. Дан куб АВСDА1В1С1D1. Докажите, что плоскости АВС1 и А1В1D перпендикулярны. № 191. D А В С
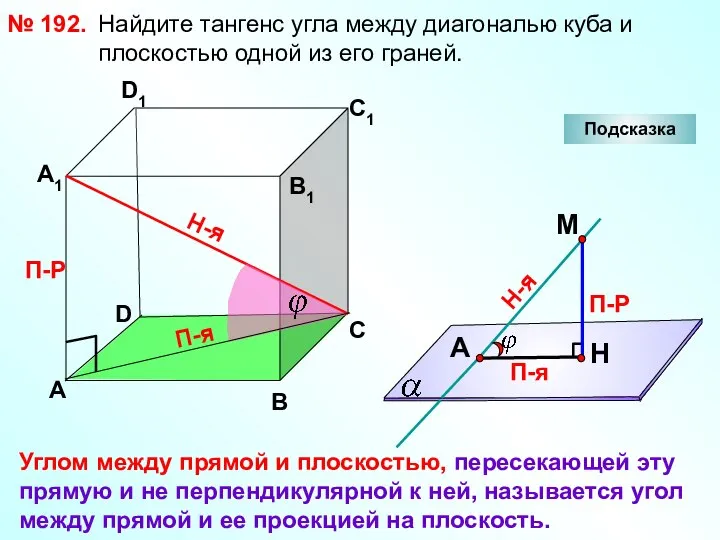
- 28. Найдите тангенс угла между диагональю куба и плоскостью одной из его граней. № 192. D А
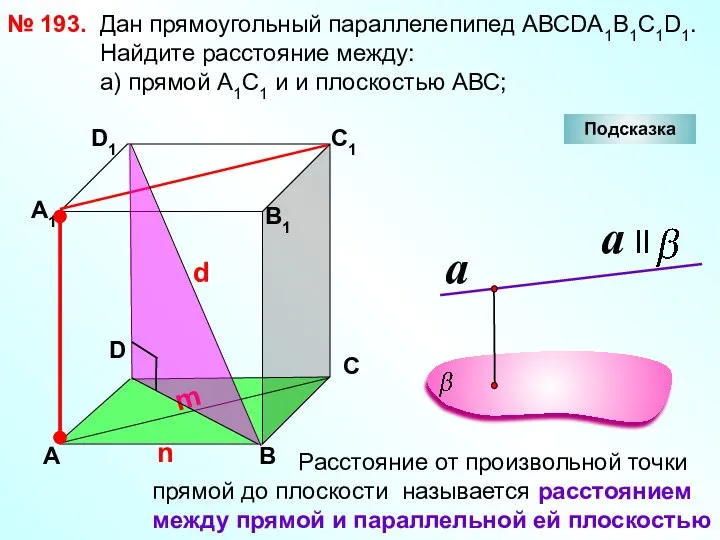
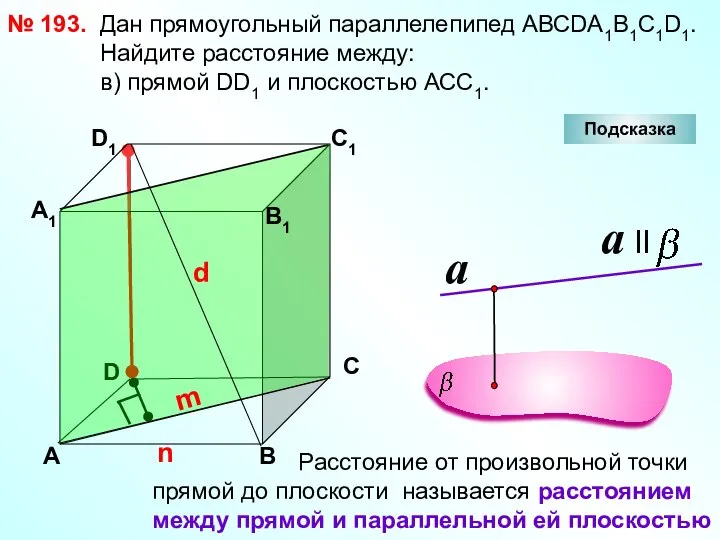
- 29. № 193. D А В С А1 D1 С1 В1 Подсказка Дан прямоугольный параллелепипед АВСDА1В1С1D1. Найдите
- 30. № 193. D А В С А1 D1 С1 В1 Подсказка Дан прямоугольный параллелепипед АВСDА1В1С1D1 Найдите
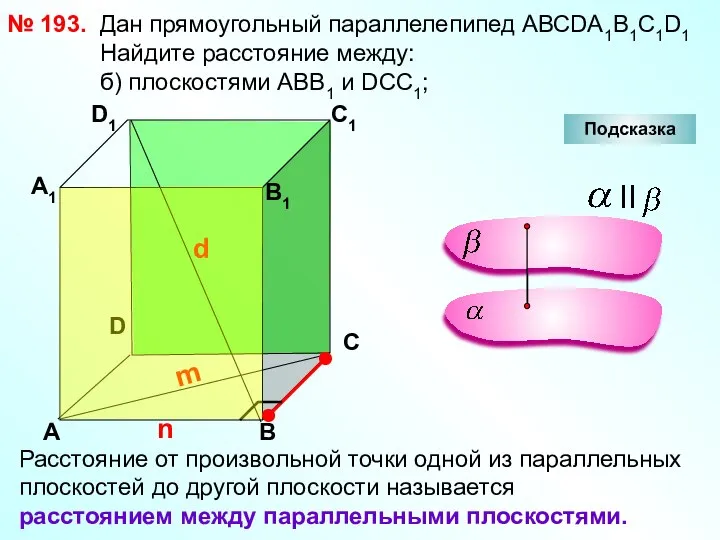
- 31. № 193. D А В С А1 D1 С1 Дан прямоугольный параллелепипед АВСDА1В1С1D1. Найдите расстояние между:
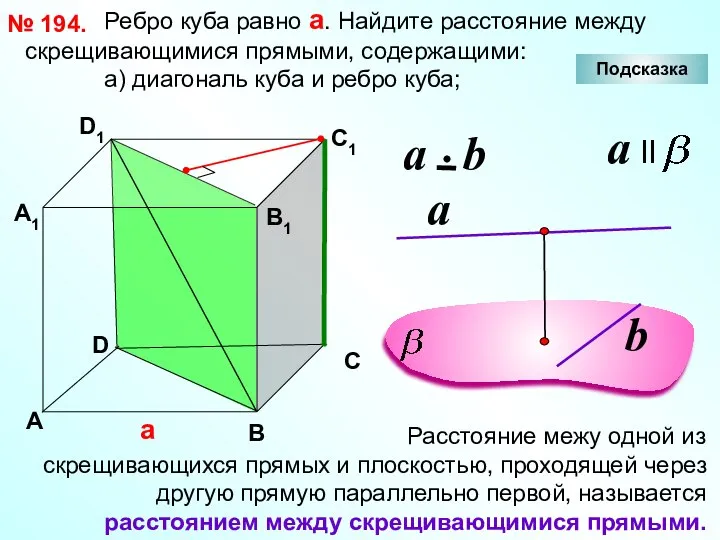
- 32. Ребро куба равно а. Найдите расстояние между скрещивающимися прямыми, содержащими: а) диагональ куба и ребро куба;
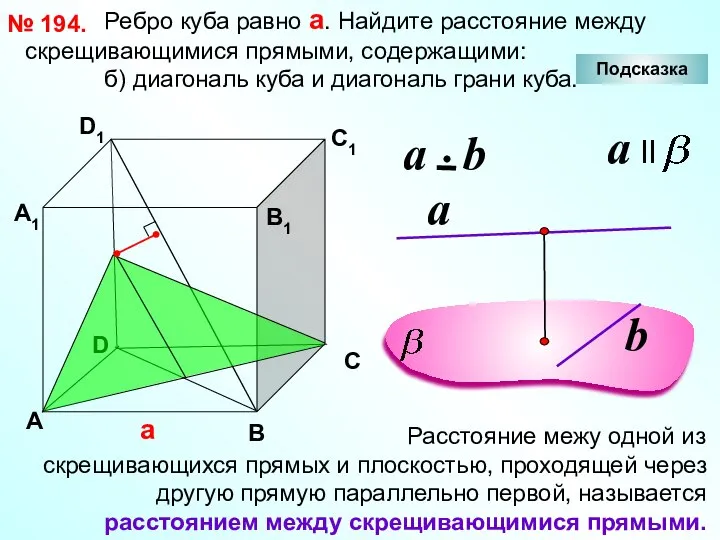
- 33. Ребро куба равно а. Найдите расстояние между скрещивающимися прямыми, содержащими: б) диагональ куба и диагональ грани
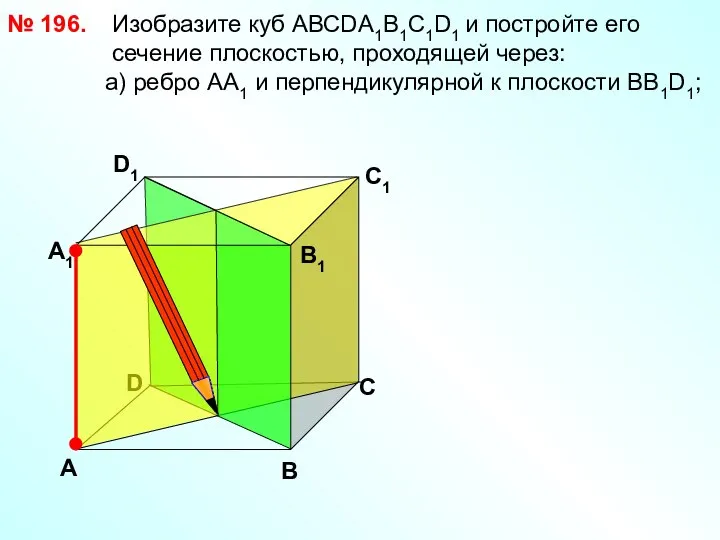
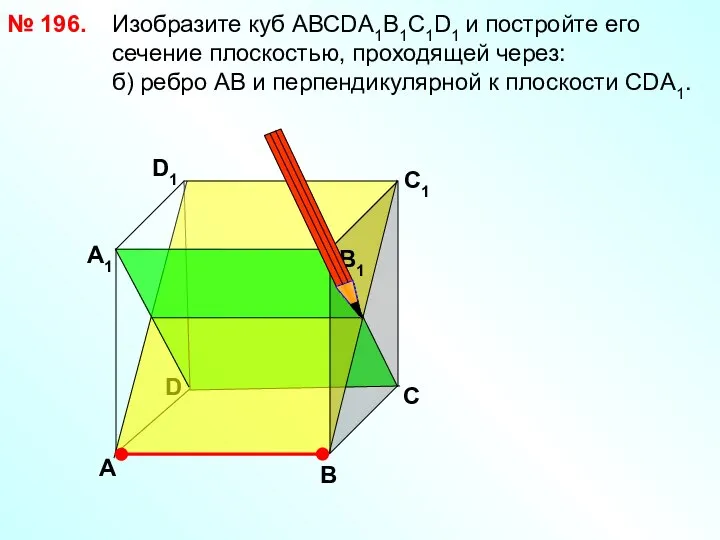
- 34. № 196. D В D1 С1 Изобразите куб АВСDА1В1С1D1 и постройте его сечение плоскостью, проходящей через:
- 35. № 196. Изобразите куб АВСDА1В1С1D1 и постройте его сечение плоскостью, проходящей через: б) ребро АВ и
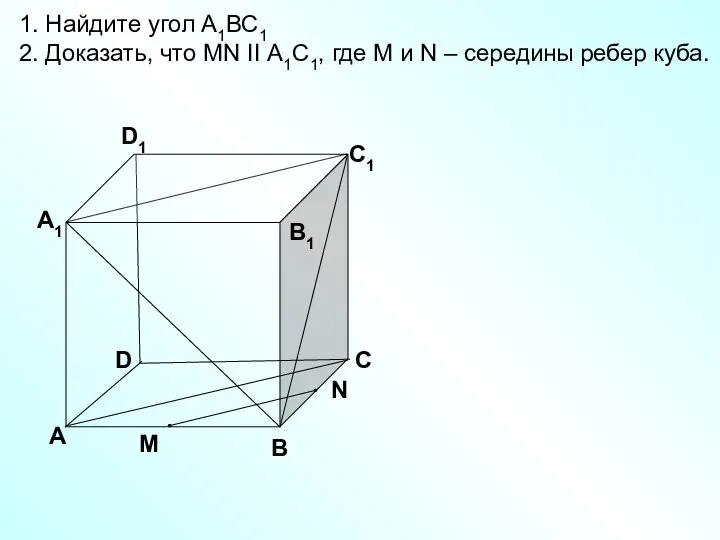
- 36. D А В С А1 D1 С1 В1 1. Найдите угол А1ВС1 2. Доказать, что MN
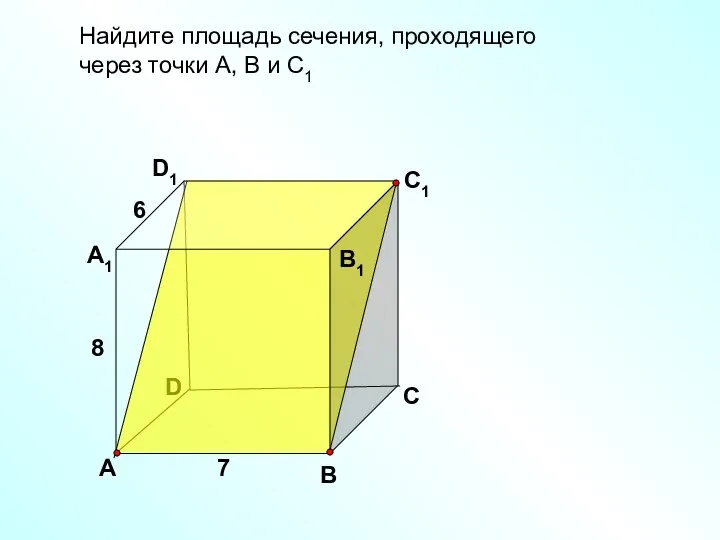
- 37. Найдите площадь сечения, проходящего через точки А, В и С1 D В D1 С1 А А1
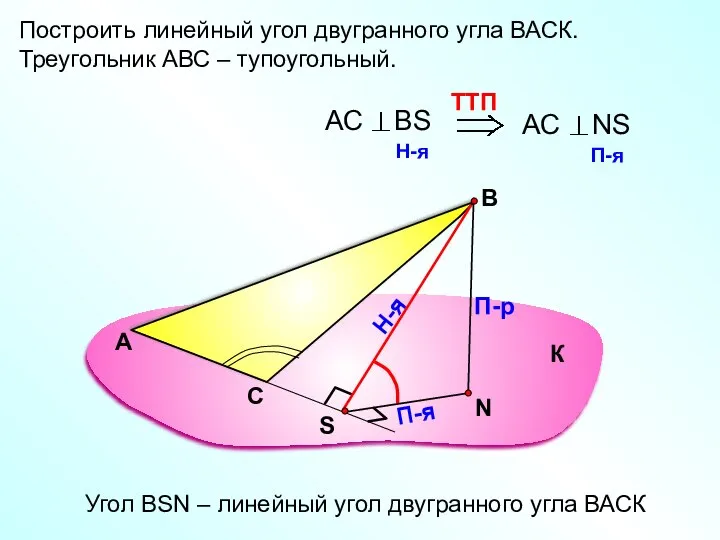
- 38. Построить линейный угол двугранного угла ВАСК. Треугольник АВС – тупоугольный. А В П-р Н-я П-я Угол
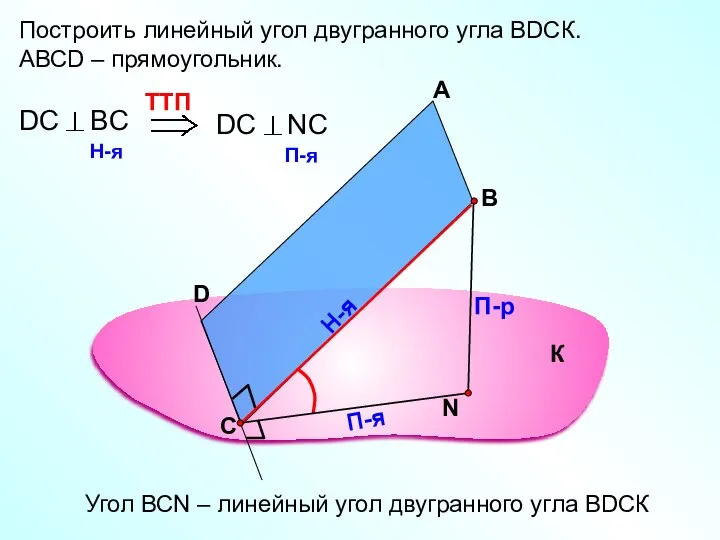
- 39. Построить линейный угол двугранного угла ВDСК. АВСD – прямоугольник. А В П-р Н-я П-я Угол ВСN
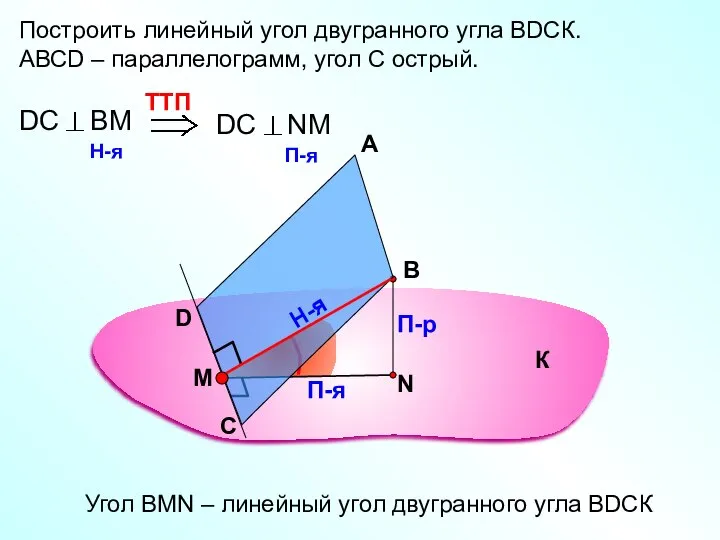
- 40. Построить линейный угол двугранного угла ВDСК. АВСD – параллелограмм, угол С острый. А В П-р П-я
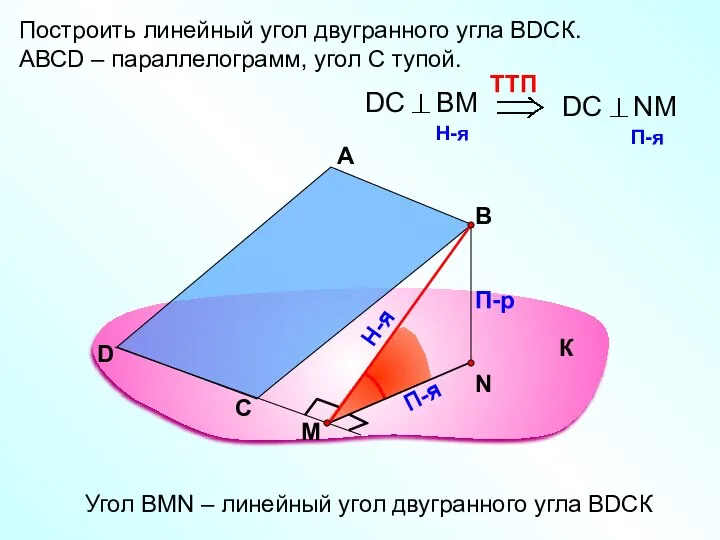
- 41. Построить линейный угол двугранного угла ВDСК. АВСD – параллелограмм, угол С тупой. А В П-р П-я
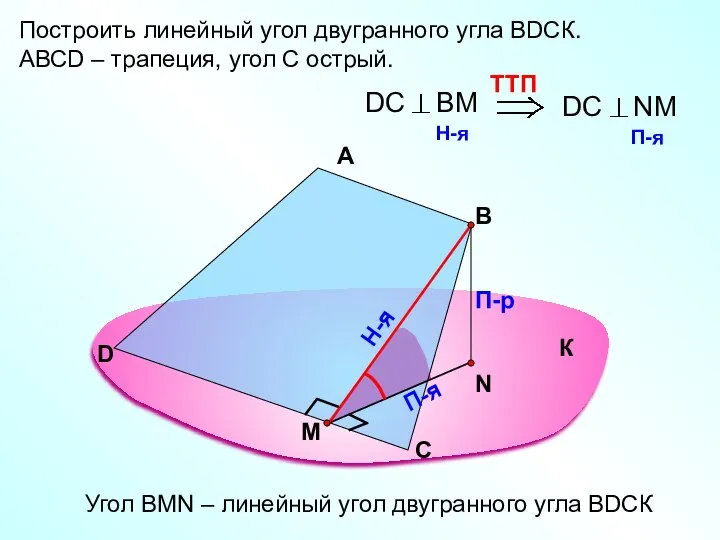
- 42. Построить линейный угол двугранного угла ВDСК. АВСD – трапеция, угол С острый. А В П-р П-я
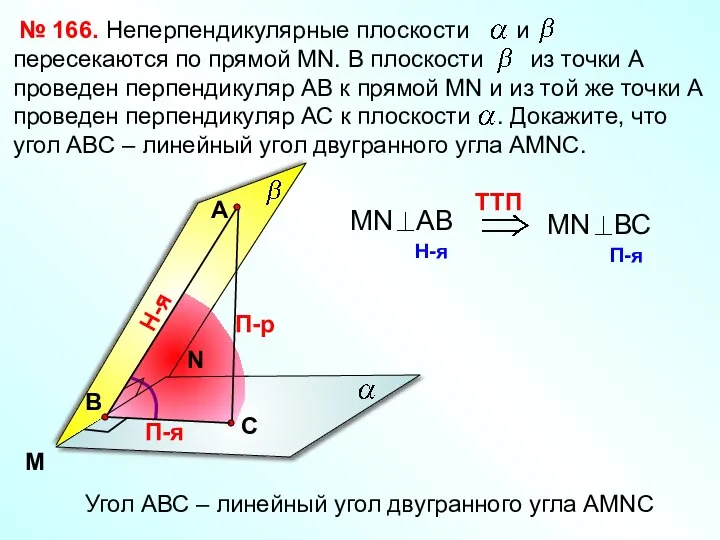
- 43. № 166. M N А П-р Н-я П-я Угол АВС – линейный угол двугранного угла АМNC
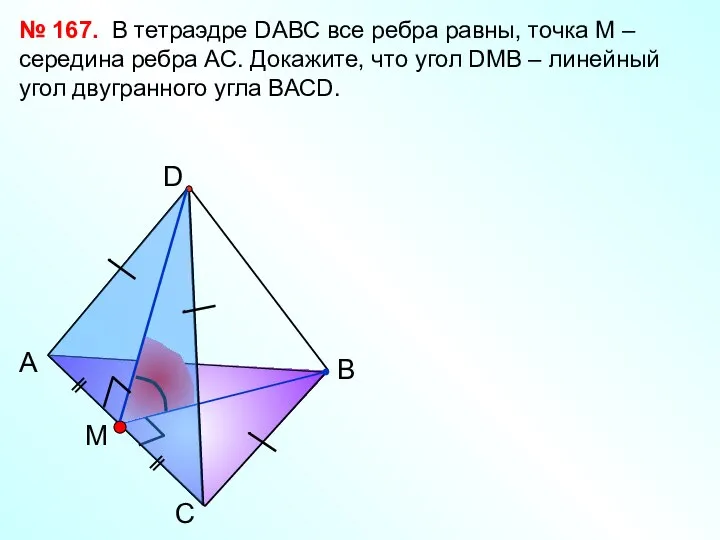
- 44. С А В D M В тетраэдре DАВС все ребра равны, точка М – середина ребра
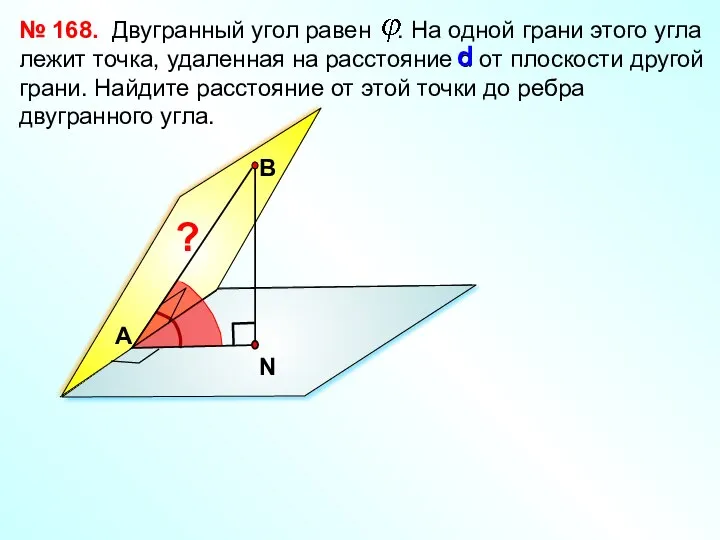
- 45. Двугранный угол равен . На одной грани этого угла лежит точка, удаленная на расстояние d от
- 47. Скачать презентацию

 Презентация на тему Деление многозначного числа на однозначное
Презентация на тему Деление многозначного числа на однозначное  Графическое представление газовых законов
Графическое представление газовых законов Решение целых уравнений. 9 класс
Решение целых уравнений. 9 класс Построение графиков функций при решении квадратных уравнений
Построение графиков функций при решении квадратных уравнений Взаимное расположение прямых и плоскостей
Взаимное расположение прямых и плоскостей Тренажёр. Табличное умножение
Тренажёр. Табличное умножение Сфера и шар
Сфера и шар Граф – набор точек, некоторые из которых соединены линиями
Граф – набор точек, некоторые из которых соединены линиями Спин и расширенное супервремя
Спин и расширенное супервремя Значение степени возведение в степень
Значение степени возведение в степень Анализ геометрической формы предмета
Анализ геометрической формы предмета Эндогенность. Инструментальные переменные
Эндогенность. Инструментальные переменные Свойства функций . 9 класс
Свойства функций . 9 класс Решение задач на проценты
Решение задач на проценты Уравнение. Правила решения уравнения
Уравнение. Правила решения уравнения Стереометрия 1. ЕГЭ
Стереометрия 1. ЕГЭ Знакомая незнакомка. Парабола
Знакомая незнакомка. Парабола Сложение и вычитание в пределах 100
Сложение и вычитание в пределах 100 Степенная функция. Определение
Степенная функция. Определение Сумма углов треугольника
Сумма углов треугольника Уравнение прямой
Уравнение прямой Основные правила построения сечений
Основные правила построения сечений Графики степенных функций
Графики степенных функций Степенная функция
Степенная функция Неопределённый интеграл. Элементы интегрального исчисления
Неопределённый интеграл. Элементы интегрального исчисления Решение систем линейных уравнений при помощи компьютерных технологий
Решение систем линейных уравнений при помощи компьютерных технологий Тренировка интеллекта
Тренировка интеллекта Презентация на тему Степень с рациональным показателем (9 класс)
Презентация на тему Степень с рациональным показателем (9 класс)