Слайд 2Метод Гаусса – это метод последовательного исключения переменных
Систему уравнений приводят к эквивалентной

ей системе с треугольной матрицей. Это называется прямым ходом.
Из полученной треугольной системы переменные находят с помощью последовательных подстановок. Это называется обратным ходом.
Слайд 3При выполнении прямого хода используют следующие преобразования:
Умножение или деление коэффициентов свободных членов

на одно и то же число;
Сложение и вычитание уравнений;
Перестановка уравнений системы;
Исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю.
Слайд 4Решить систему уравнений методом Гаусса
Нужно записать расширенную матрицу системы
Вертикальная черта внутри матрицы не

несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
Слайд 5Матрица системы – это матрица, составленная только из коэффициентов при неизвестных.
Расширенная матрица системы –

это та же матрица системы плюс столбец свободных членов, в данном случае.
Слайд 6Решение.
Умножим первую строку на (-2)

Слайд 7ко второй строке прибавим первую строку умноженную на -2

Слайд 8Разделим опять первую строку на (-2)
строка, которую ПРИБАВЛЯЛИ – не изменилась.
Всегда меняется строка, К КОТОРОЙ

ПРИБАВЛЯЮТ.
Слайд 9Цель элементарных преобразований –
привести матрицу к ступенчатому виду. Сам термин «ступенчатый вид» не

вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный
Слайд 10В результате элементарных преобразований получена эквивалентная исходной система уравнений
Выполняем обратный ход, т.е. подстановку

в первое уравнение вместо у,
х =-5+у
х=-5+1
х=-4
Ответ: (-4; 1)
Слайд 11Решить систему уравнений методом Гаусса
Решение.
Переставим третье уравнение на место первого и запишем

расширенную матрицу:
Слайд 12Чтобы в первом столбце получить а2=а3=0, умножим 1-ю строку сначала на 3,

а затем на 2 и вычтем результаты из 2-й и 3-й строк
Слайд 13Разделим 2-ю строку на 8, полученные результаты умножим на 3 и вычтем

из 3-й строки












 Линейная функция и её график
Линейная функция и её график Презентация по математике "Выполните задание !" -
Презентация по математике "Выполните задание !" -  ЕГЭ Профиль. Решение задания №7
ЕГЭ Профиль. Решение задания №7 Теоремы о пределах. Нахождение пределов
Теоремы о пределах. Нахождение пределов Квадратичная функция
Квадратичная функция лекция 2
лекция 2 Презентация на тему История теоремы Пифагора
Презентация на тему История теоремы Пифагора  Некоторые свойства прямоугольных треугольников
Некоторые свойства прямоугольных треугольников Тригонометрические функции суммы и разности двух углов, двойного угла. Формулы половинного угла
Тригонометрические функции суммы и разности двух углов, двойного угла. Формулы половинного угла Чтение графика функций
Чтение графика функций Прямые измерения, косвенные, совокупные и совместные
Прямые измерения, косвенные, совокупные и совместные Основы геометрии
Основы геометрии Теорема Пифагора
Теорема Пифагора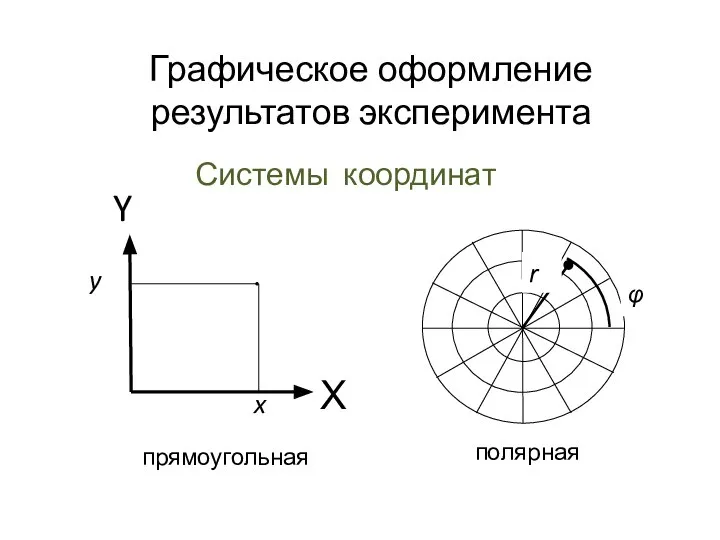 Графическое оформление результатов эксперимента
Графическое оформление результатов эксперимента Раскрытие скобок
Раскрытие скобок Первый замечательный предел
Первый замечательный предел Решение задач. Касательная к окружности
Решение задач. Касательная к окружности Надежность производственных и технологических систем. Математические модели в теории надежности
Надежность производственных и технологических систем. Математические модели в теории надежности Решение задач на применение аксиом стереометрии и их следствий
Решение задач на применение аксиом стереометрии и их следствий Игра - тренажёр Собери солнышко. Состав чисел 11, 12, 13. 1 класс
Игра - тренажёр Собери солнышко. Состав чисел 11, 12, 13. 1 класс Названия компонентов арифметических действий, знаки действий
Названия компонентов арифметических действий, знаки действий Функция нескольких действительных переменных. Условный экстремум
Функция нескольких действительных переменных. Условный экстремум Математика. 2 класс. Задачи
Математика. 2 класс. Задачи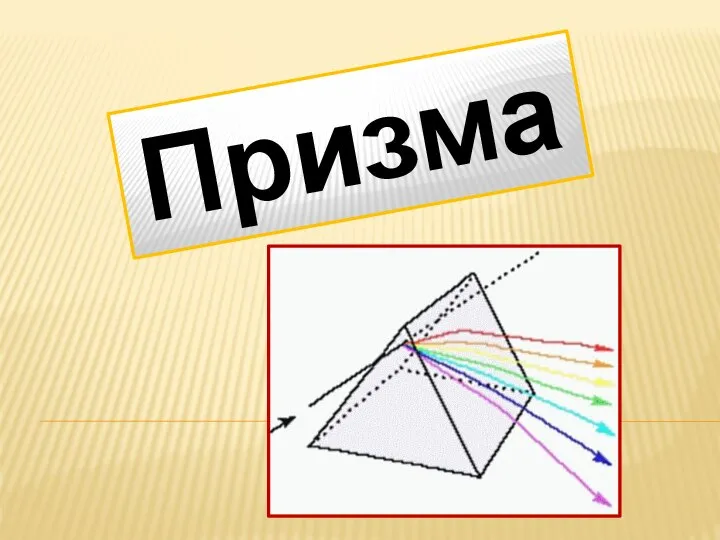 Призма. Дисперсия света в призме
Призма. Дисперсия света в призме Презентация на тему Действия с рациональными числами
Презентация на тему Действия с рациональными числами  Новый год и правильные многогранники
Новый год и правильные многогранники Задачи на движение. Обобщающий урок
Задачи на движение. Обобщающий урок Сложение и вычитание десятичных дробей. 15 февраля в истории Кубани
Сложение и вычитание десятичных дробей. 15 февраля в истории Кубани