Слайд 2Экстремум функции двух переменных
Пример 1. Найдите экстремумы функции
Находим частные производные
2. Объединим в

систему уравнений и решим ее (через замену, поскольку она нелинейна)
Мы нашли предполагаемые точки экстремума:
3. Проверим их на наличие экстремума. Найдем вторые производные
Слайд 3Экстремум функции двух переменных
Пример 1. Найдите экстремумы функции
4. Сформируем дискриминант и найдем

его значения для каждой точки
5. Точки N и К – точки максимума
Слайд 4Экстремум функции двух переменных
Посмотрим на график функции
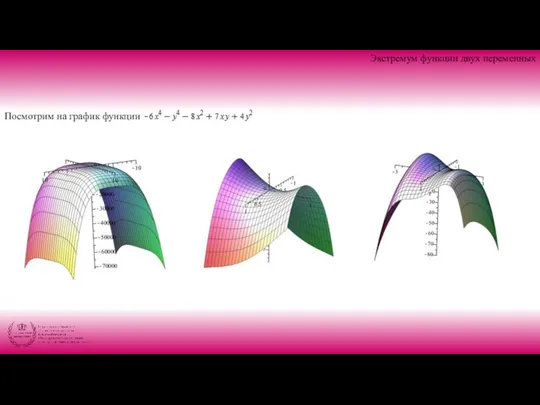
Слайд 5Экстремум функции двух переменных
Пример 2. Найдите экстремумы функции
Сформируем функцию Лагранжа
2. Найдем частные

производные от функции Лагранжа
3. Приравняем их к 0 и найдем стационарные точки
4. Посчитаем вторые производные и определитель
по формуле




 ОГЭ 2022 Математика. Вариант 15
ОГЭ 2022 Математика. Вариант 15 Лабиринты. Решение найденных лабиринтов и поиск универсальных правил
Лабиринты. Решение найденных лабиринтов и поиск универсальных правил Шар и сфера
Шар и сфера О числах
О числах Содержание кривых участков пути. Переходные кривые
Содержание кривых участков пути. Переходные кривые Числа 1 - 4. (1 класс)
Числа 1 - 4. (1 класс) Призма. Площади поверхностей. Объем призмы
Призма. Площади поверхностей. Объем призмы Задача по математике (4 класс, задание 85.1)
Задача по математике (4 класс, задание 85.1) Математическая статистика (среднее арифметическое, мода, размах, медиана) комбинаторика
Математическая статистика (среднее арифметическое, мода, размах, медиана) комбинаторика uravnenie_urok_2
uravnenie_urok_2 Примеры задач с таблицами истинности
Примеры задач с таблицами истинности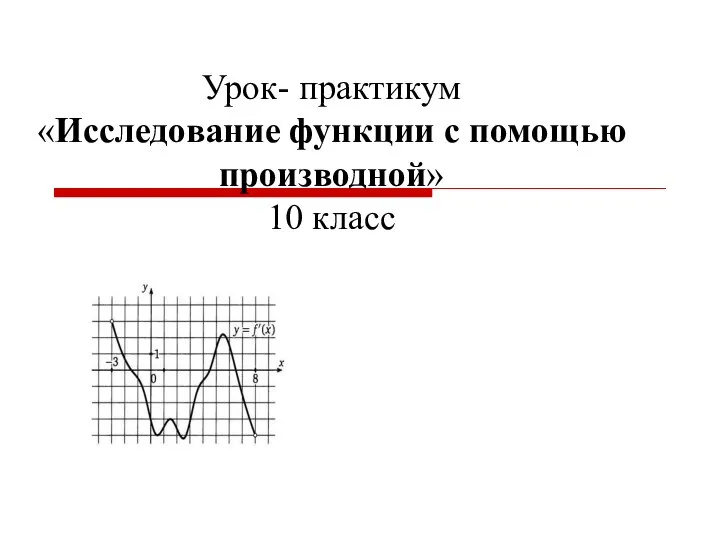 Исследование функции с помощью производной
Исследование функции с помощью производной Логарифм числа
Логарифм числа 6f20c70ecac24a5caad72fa88b388b76
6f20c70ecac24a5caad72fa88b388b76 Презентация на тему Порядок выполнения действий в выражениях со скобками
Презентация на тему Порядок выполнения действий в выражениях со скобками  Интегрированный урок. Применение производной в физике и технике. 11 класс
Интегрированный урок. Применение производной в физике и технике. 11 класс Пперпендикулярные прямые
Пперпендикулярные прямые Ряды динамики
Ряды динамики Показательная функция
Показательная функция Многогранники
Многогранники Математическое моделирование
Математическое моделирование Применение подобия к доказательству теорем и решению задач. Урок 38
Применение подобия к доказательству теорем и решению задач. Урок 38 Логарифмическая линия в ЕГЭ
Логарифмическая линия в ЕГЭ Подобие. Коэффициент подобия
Подобие. Коэффициент подобия Міри центральної тенденції
Міри центральної тенденції Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Презентация на тему Единицы измерения
Презентация на тему Единицы измерения  Определение двойного интеграла
Определение двойного интеграла