Содержание
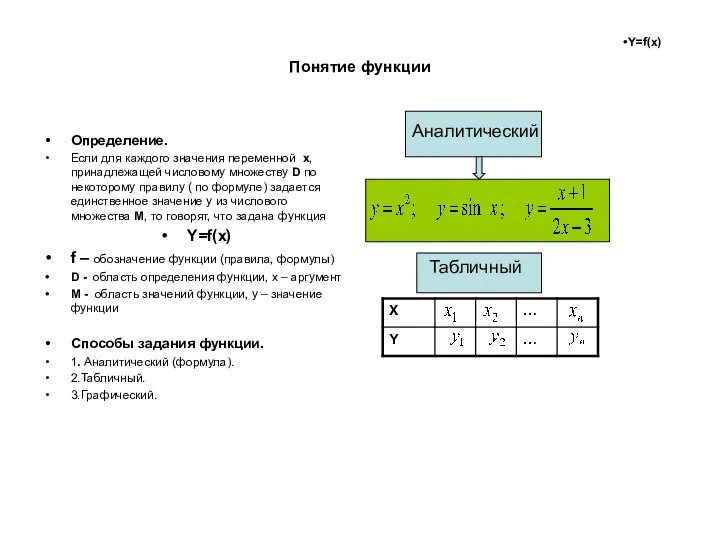
- 2. Понятие функции Определение. Если для каждого значения переменной x, принадлежащей числовому множеству D по некоторому правилу
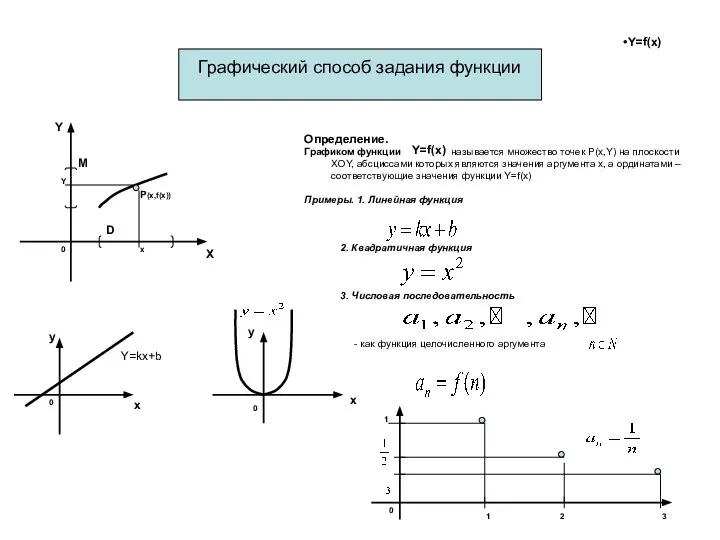
- 3. Графический способ задания функции Определение. Графиком функции называется множество точек P(x,Y) на плоскости XOY, абсциссами которых
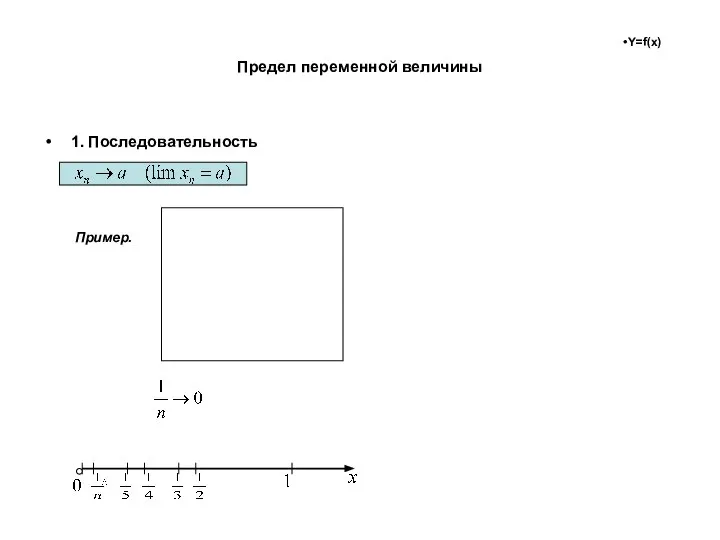
- 41. Предел переменной величины 1. Последовательность Пример.
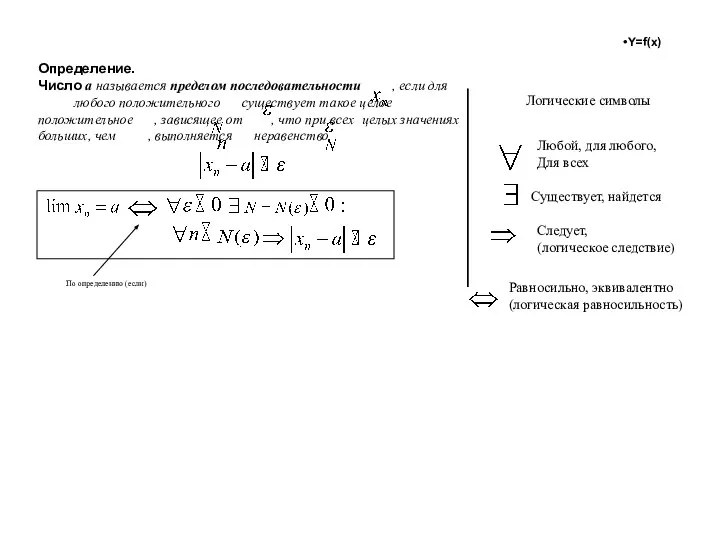
- 42. Определение. Число a называется пределом последовательности , если для любого положительного существует такое целое положительное ,
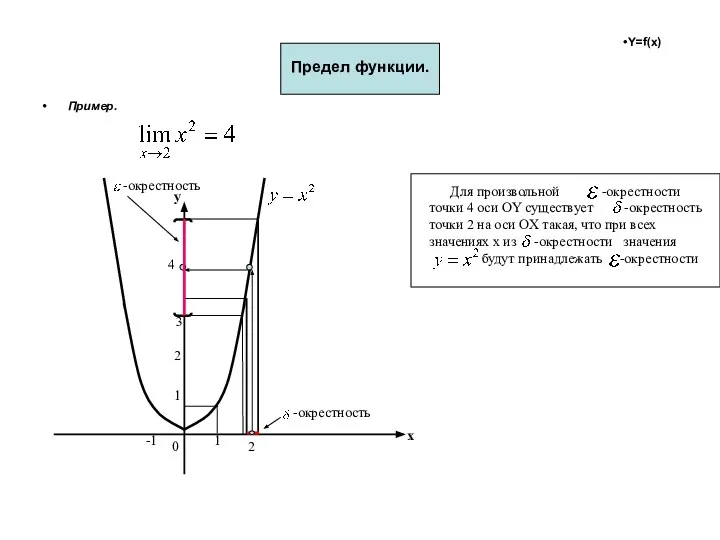
- 43. Предел функции. Пример. х y 0 1 2 1 2 3 4 -1 -окрестность -окрестность Для
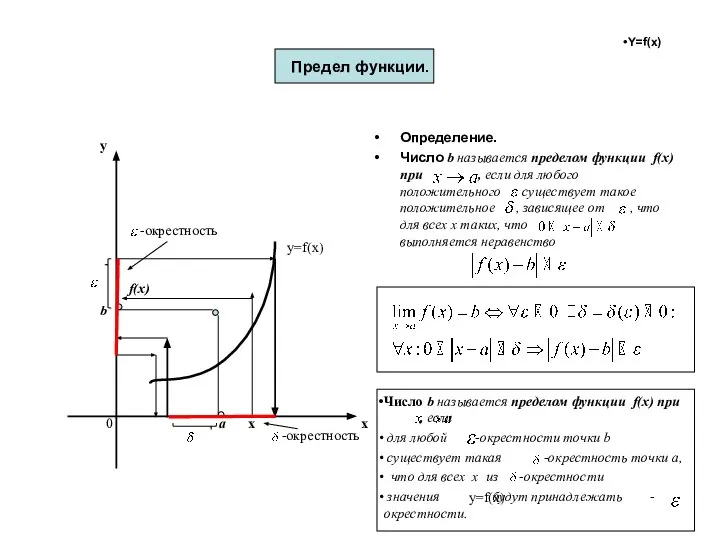
- 44. Число b называется пределом функции f(x) при , если для любой -окрестности точки b существует такая
- 45. Частный случай предела. Определение. Функция f(x) называется бесконечно малой при , если Функция f(x) называется бесконечно
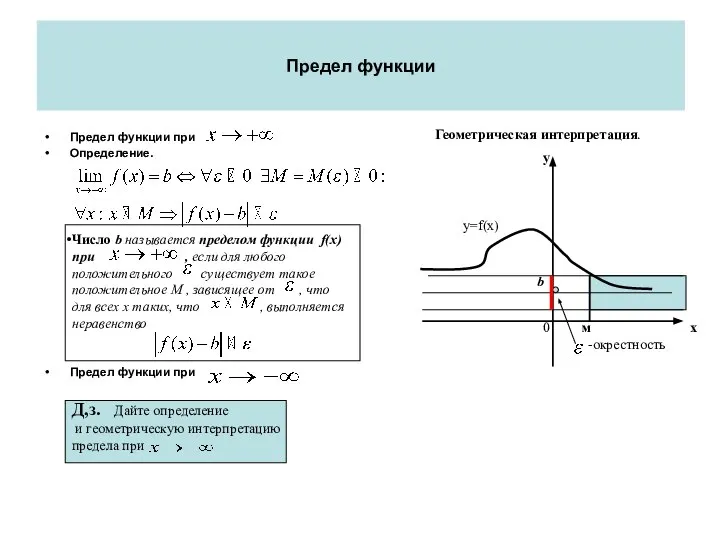
- 46. Предел функции Предел функции при Определение. Предел функции при Число b называется пределом функции f(x) при
- 47. Предел функции Односторонние пределы. 1. Правосторонний предел в точке. Определение. Число b называется правосторонним пределом функции
- 49. Скачать презентацию



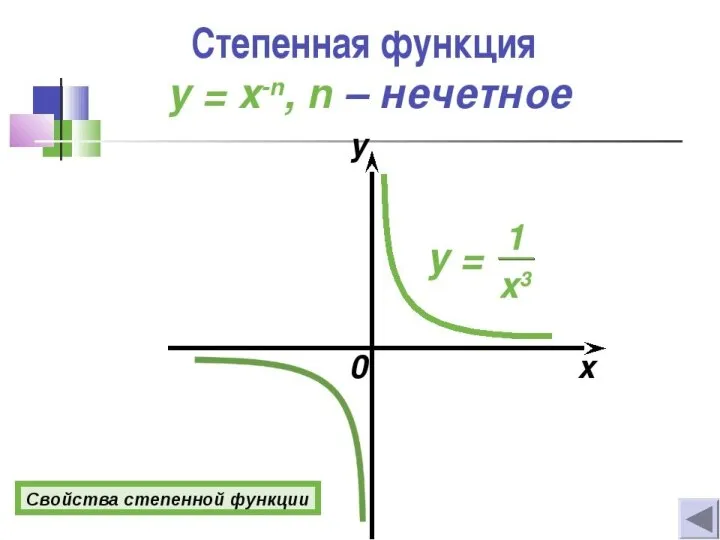
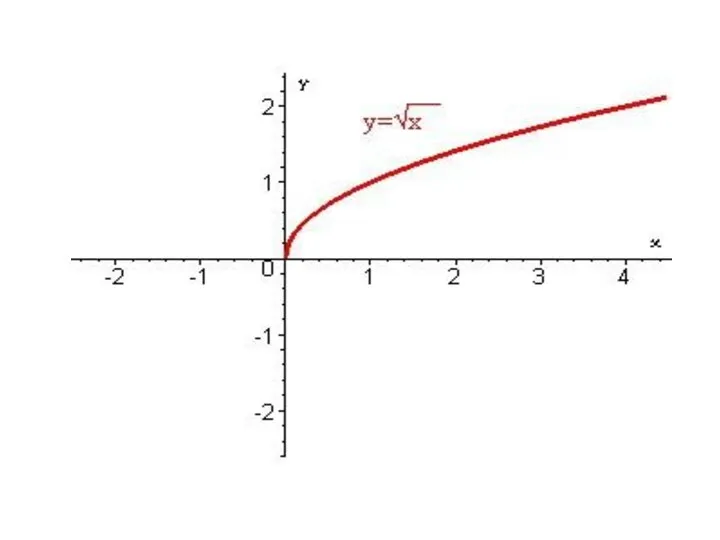
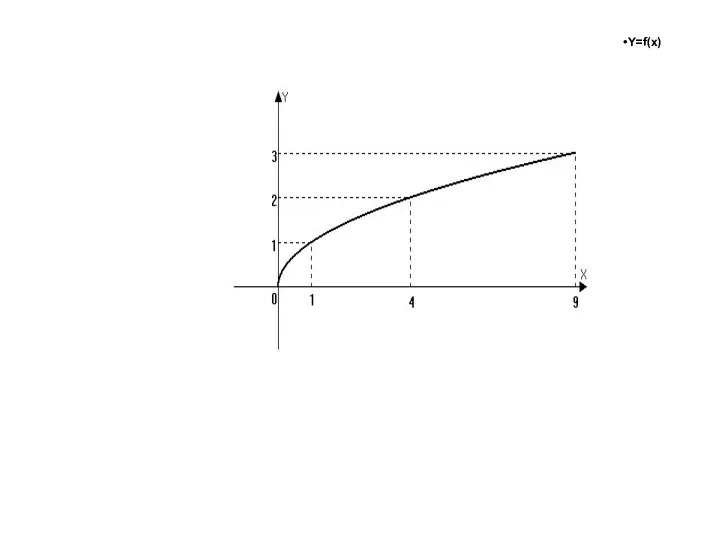
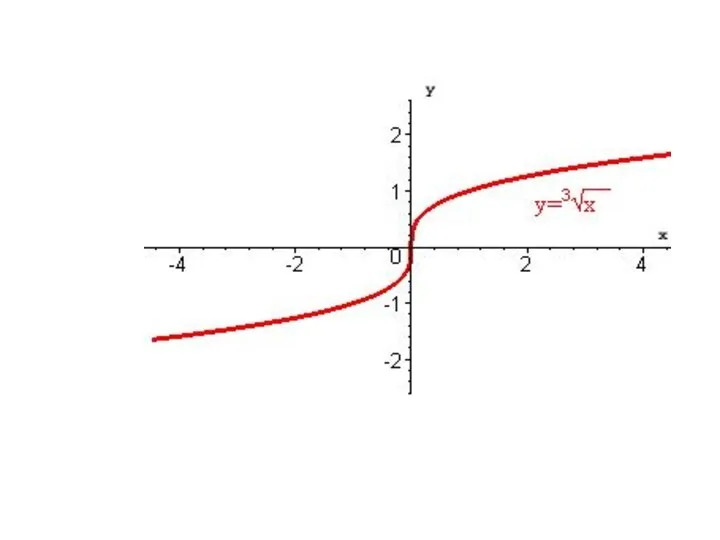







 Углы в пространстве. Перпендикулярность плоскостей
Углы в пространстве. Перпендикулярность плоскостей Умножение - 3
Умножение - 3 Правильный многоугольник
Правильный многоугольник Математика. Закрепление изученного материала. 4 класс
Математика. Закрепление изученного материала. 4 класс Электронные таблицы. Построение графиков и диаграмм
Электронные таблицы. Построение графиков и диаграмм Объем наклонной призмы
Объем наклонной призмы Перпендикулярные прямые
Перпендикулярные прямые Экономический факторный анализ. Теорема о среднем
Экономический факторный анализ. Теорема о среднем Прогрессии. Лекция №2
Прогрессии. Лекция №2 Теорема Пифагора
Теорема Пифагора Сумма углов треугольника
Сумма углов треугольника Математические приемы быстрого счета (лайфхаки)
Математические приемы быстрого счета (лайфхаки) Коллекция игр. 1 класс
Коллекция игр. 1 класс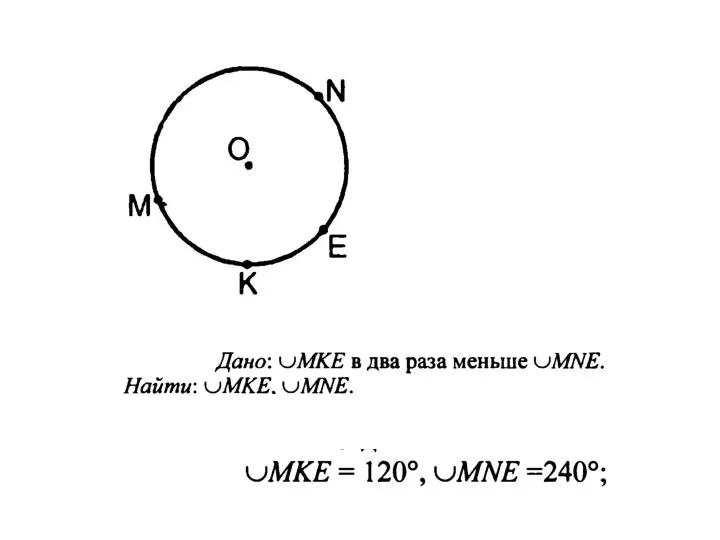 Теорема о вписанном угле
Теорема о вписанном угле Методическая разработка по математике. Тема: Треугольники
Методическая разработка по математике. Тема: Треугольники Табличное представление информации
Табличное представление информации Равносильность формул логики. Законы логики
Равносильность формул логики. Законы логики Арифметическая прогрессия. Всё в твоих руках
Арифметическая прогрессия. Всё в твоих руках Устный счёт
Устный счёт Геометрия треугольника
Геометрия треугольника Презентация на тему Математические головоломки (3 класс)
Презентация на тему Математические головоломки (3 класс)  Первый признак параллельности прямых
Первый признак параллельности прямых Пирамида
Пирамида Час занимательной математики. 5 класс
Час занимательной математики. 5 класс Построить линейный угол двугранного угла
Построить линейный угол двугранного угла Проценты. Задания
Проценты. Задания Презентация на тему Понятие площади и объёма
Презентация на тему Понятие площади и объёма  Геометрическое решение задачи о расстояниях между точками
Геометрическое решение задачи о расстояниях между точками