Слайд 2 ДРЕВНИЕ ГРЕКИ СЧИТАЛИ ОКРУЖНОСТЬ СОВЕРШЕННЕЙШЕЙ
И «САМОЙ КРУГЛОЙ» ФИГУРОЙ.
И В
НАШЕ ВРЕМЯ В НЕКОТОРЫХ
СИТУАЦИЯХ, КОГДА ХОТЯТ ДАТЬ
ОСОБУЮ ОЦЕНКУ, ИСПОЛЬЗУЮТ СЛОВО «КРУГЛЫЙ», КОТОРОЕ СЧИТАЕТСЯ СИНОНИМОМ СЛОВА ПОЛНЕЙШИЙ. ЕЩЕ В ДРЕВНОСТИ ЛЮДЯМ БЫЛИ ИЗВЕСТНЫ МНОГИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ, В ТОМ ЧИСЛЕ ОКРУЖНОСТЬ. ОБ ЭТОМ СВИДЕТЕЛЬСТВУЮТ АРХЕОЛОГИЧЕСКИЕ
РАСКОПКИ. ОКРУЖНОСТЬ –
САМАЯ ПРОСТАЯ КРИВАЯ ЛИНИЯ.
Слайд 3ЦЕЛИ КУРСА:
Развитие устойчивого интереса учащихся к изучению математики.
Формирование умений решать задачи

на вписанные и описанные окружности.
Воспитание понимания, что математика является инструментом познания окружающего мира.
Определение уровня способности учащихся и их готовности в дальнейшем к обучению в школе и успешной сдачи ГИА.
Слайд 4ИЗУЧЕНИЕ ДАННОГО ЭЛЕКТИВНОГО КУРСА ПОЗВОЛИТ РЕАЛИЗОВАТЬ СЛЕДУЮЩИЕ ЗАДАЧИ:
Систематизировать ранее полученные знания по

решению планиметрических задач на вписанные и описанные окружности.
Познакомить учащихся с различными типами задач и различными способами их решения.
Развивать логическое мышление учащихся, обогащать и расширять математический кругозор учащихся.
Научить применять математические знания в решении повседневных жизненных задач бытового характера
Слайд 5ОБРАЗОВАТЕЛЬНЫЙ ПРОДУКТ: РЕШЕНИЯ ЗАДАЧ РАЗЛИЧНОГО ТИПА, СОЗДАНИЕ СПРАВОЧНОГО МАТЕРИАЛА, ПРЕЗЕНТАЦИИ.
Этапы изучения курса:

1 этап: повторение основных теоретических знаний. Содержание данного этапа указано для каждого раздела.
2 этап: решение простейших задач. Контроль работы учащихся в группах и парах. Работа по дидактическому материалу.
3 этап: решение трудных и нестандартных задач. Введение таких задач необходимо, так как решение одной сложной задачи может заменить решение нескольких простейших задач. Контроль работы учащихся на данном этапе осуществляется учителем.
4 этап: предварительный контроль в форме тестовой и зачетных работ учащихся.
5 этап: решение задач по материалам ГИА, составление справочного материала.
Слайд 6РАЗДЕЛ 1. «ОКРУЖНОСТЬ И ЕЁ ЭЛЕМЕНТЫ» (2 ЧАСА)
*основные свойства окружности;
*замечательные свойства окружности

(геометрические места точек);
*формулы площади круга и длины окружности, площади кругового сектора, длины дуги в несколько градусов;
*различные случай касания окружностей;
*теорема о пересекающихся хордах;
*теорема о длинах касательных, проведенных из одной точки к окружности;
*углы: между касательной и хордой; между двумя пересекающимися хордами; между двумя секущими; между касательной и секущей; между двумя касательными;
*углы, связанные с окружностью (центральные углы, вписанные углы);
Слайд 7РАЗДЕЛ 2. «ВПИСАННАЯ ОКРУЖНОСТЬ» (4 ЧАСА)
* теорема об окружности, вписанной в треугольник;

* выражение площади треугольника через радиус вписанной окружности;
* свойство и признак описанного четырехугольника, и его применение при решении задач;
*площадь описанного четырехугольника.
Слайд 8РАЗДЕЛ 3. «ОПИСАННАЯ ОКРУЖНОСТЬ» (4 ЧАСА)
* теорема об окружности, описанной около треугольника;

* следствие из теоремы синусов о радиусе окружности, описанной около треугольника;
* свойство и признак вписанного четырехугольника, и его применение при решении задач;
* формула Герона, для четырехугольника, около которого можно описать окружность.
Слайд 9РАЗДЕЛ 4. «КОМБИНАЦИЯ ОКРУЖНОСТЕЙ» (2 ЧАСА)
* комбинация окружностей, вписанная и описанная

около треугольника и четырехугольника.
* площадь четырехугольника являющегося одновременно вписанным и описанным.
*взаимное расположение двух окружностей;
*ключевая задача об общей касательной двух касающихся окружностей.
Слайд 10ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ:
- овладение знаниями и умениями в области геометрии, необходимыми для изучения

естественнонаучных дисциплин, продолжения образования и освоения избранной специальности на современном уровне;
-формирование навыков обобщения и систематизации теоретических знаний для решения задач;
-развитие логического мышления, алгоритмической культуры, математического мышления и интуиции, необходимых для успешной адаптации к реальной жизни и выбора профессии;
- формирование навыков исследовательской деятельности, постановки и решения проблемных вопросов; умение сравнивать, анализировать, рассуждать, выдвигать гипотезы, доказывать, делать выводы, творчески подходить к любому делу;
- формирование навыков самообразования, критического мышления, самоорганизации и самоконтроля, работы в команде.
Слайд 11Мир, в котором мы живём, наполнен геометрией домов и улиц, гор и

полей, творениями природы и человека. Лучше ориентироваться в нём, открывать новое, понимать красоту и мудрость окружающего мира поможет нам хорошее знание предмета геометрия. Великий английский учёный Исаак Ньютон сказал: «Геометрия за то и прославляется, что, заимствовав извне столь мало основных положений, она столь много достигает».










 Параллельный перенос
Параллельный перенос Логарифмические уравнения. Обобщающий урок
Логарифмические уравнения. Обобщающий урок Презентация на тему Иррациональные уравнения
Презентация на тему Иррациональные уравнения  Задачи на уменьшение числа в несколько раз
Задачи на уменьшение числа в несколько раз Формулы сокращенного умножения и их применение
Формулы сокращенного умножения и их применение Золотое сечение
Золотое сечение Эскизы кривых на плоскости, заданных параметрически
Эскизы кривых на плоскости, заданных параметрически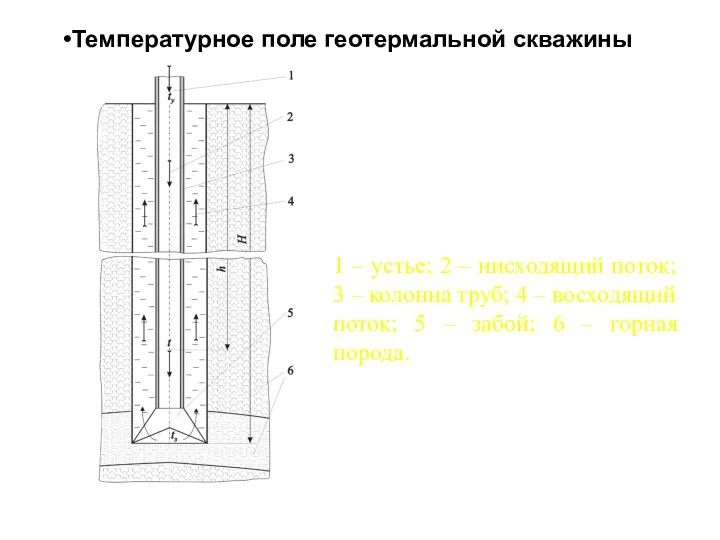 Температурное поле геотермальной скважины
Температурное поле геотермальной скважины Числа - близнецы
Числа - близнецы Презентация на тему Медиана
Презентация на тему Медиана  Поле чудес. Геометрия
Поле чудес. Геометрия Пересечение линии и поверхности. Позиционные задачи. (Лекция 8.2)
Пересечение линии и поверхности. Позиционные задачи. (Лекция 8.2) Логические элементы
Логические элементы Математическая ярмарка
Математическая ярмарка Узоры и орнаменты на посуде
Узоры и орнаменты на посуде Дифференциальные уравнения I порядка с разделяющимися переменными
Дифференциальные уравнения I порядка с разделяющимися переменными Серединный перпендикуляр
Серединный перпендикуляр Вычисление значений выражений содержащих аркфункции от функции
Вычисление значений выражений содержащих аркфункции от функции Площадь параллелограмма
Площадь параллелограмма Сложение и вычитание многозначных чисел. Игра Чей шарик?
Сложение и вычитание многозначных чисел. Игра Чей шарик? Уравнения приводимые к квадратным. Биквадратные уравнения
Уравнения приводимые к квадратным. Биквадратные уравнения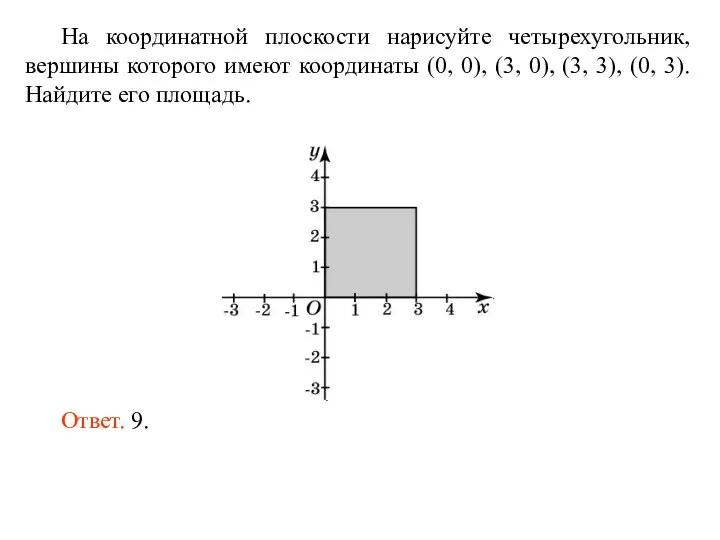 Площадь фигур
Площадь фигур Возведение в квадрат суммы и разности двух выражений
Возведение в квадрат суммы и разности двух выражений Математика. Лекция 1
Математика. Лекция 1 Интерактивный плакат Треугольник
Интерактивный плакат Треугольник Роль теории коммуникации, теории информации,теории вероятностей
Роль теории коммуникации, теории информации,теории вероятностей ПГНИУ-20.09.22 МЛ Л 4
ПГНИУ-20.09.22 МЛ Л 4 Дроби вокруг нас. 2 класс
Дроби вокруг нас. 2 класс