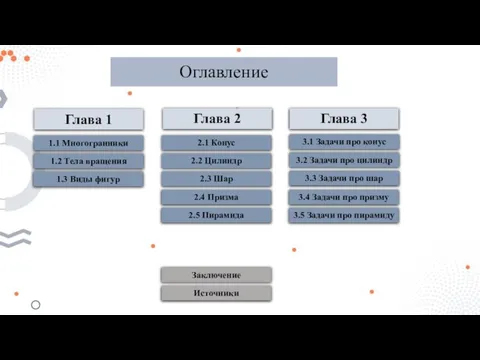
Содержание
- 2. Глава 2 2.1 Конус 2.2 Цилиндр 2.3 Шар 2.4 Призма 2.5 Пирамида Заключение Оглавление Глава 1
- 3. Глава 1: Многогранники и тела вращения Для начала стоит разобраться что же за фигура многогранник: Многогранник
- 4. 1.2 Тела вращения Для полного понимания картины, следует узнать что такое тела вращения: Тела вращения —
- 5. 1.3 Виды фигур Существует огромное множество как многогранников, так и тел вращения, но мы рассмотрим несколько
- 6. 2.1 Конус Объем конуса равен: R – радиус основания конуса, h – его высота. Формула для
- 7. 2.2 Цилиндр Все что вам необходимо сделать, что бы вычислить объём цилиндра, это найти его высоту
- 8. 2.3 Шар Объём сферы можно вычислить через радиус этой самой сферы: В этой формуле: V —
- 9. 2.4 Призма Формула для вычисления объёма призмы: V=Sh Где: S – площадь основания h – высота
- 10. 2.5 Пирамида Формула для нахождения объема пирамиды через площадь основания и высоту: Где: S — площадь
- 11. Конус. Задача 1. Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на π
- 12. Цилиндр. Задача 1. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра,
- 13. шар Задача 1. Объем шара равен 288π . Найдите площадь его поверхности, деленную на π .
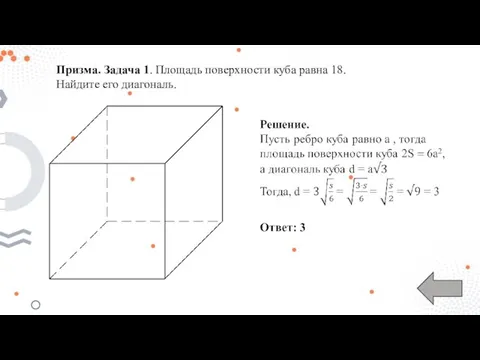
- 14. Призма. Задача 1. Площадь поверхности куба равна 18. Найдите его диагональ.
- 15. Пирамида Задача 1. Найти площадь поверхности правильной четырёхугольной пирамиды, у которой сторона основания равна 6, а
- 16. Заключение Знания полученные сегодня действительно можно считать полезными, поскольку вопросы связанные с нахождением объёма и площади
- 18. Скачать презентацию













 2.МатСтатистика-Критерии и Различия
2.МатСтатистика-Критерии и Различия Вычисление значений числовых выражений с действиями разной степени. Проверка деления умножением. 3 класс
Вычисление значений числовых выражений с действиями разной степени. Проверка деления умножением. 3 класс Презентация на тему Готфрид Вильгельм Лейбниц
Презентация на тему Готфрид Вильгельм Лейбниц  Графический диктант. Тема: Делимость чисел
Графический диктант. Тема: Делимость чисел Практическое применение площадей геометрических фигур
Практическое применение площадей геометрических фигур Государственное общеобразовательное учреждение Гимназия№49 Приморского района Санкт -Петербурга «Путешествие Алисы в страну Ма
Государственное общеобразовательное учреждение Гимназия№49 Приморского района Санкт -Петербурга «Путешествие Алисы в страну Ма Площади геометрических фигур
Площади геометрических фигур Презентация на тему Свойства степени с натуральным показателем
Презентация на тему Свойства степени с натуральным показателем  Инфекционные заболевания, их классификация и профилактика
Инфекционные заболевания, их классификация и профилактика pril1
pril1 Серединный перпендикуляр
Серединный перпендикуляр Вычисление углов между прямыми и плоскостями
Вычисление углов между прямыми и плоскостями Число или цифра 3
Число или цифра 3 Турнир знаний. Что это за формула
Турнир знаний. Что это за формула Задачи про виноград и изюм
Задачи про виноград и изюм Презентация на тему Параллельный перенос и Поворот
Презентация на тему Параллельный перенос и Поворот  Решение задач. Параллельные прямые
Решение задач. Параллельные прямые Тест по теме: Углы. Параллельные прямые. Перпендикулярные прямые
Тест по теме: Углы. Параллельные прямые. Перпендикулярные прямые Решение задач на проценты
Решение задач на проценты Факториал. Теорема
Факториал. Теорема Векторы. Действия с векторами
Векторы. Действия с векторами Применение теории паркета для доказательства свойств и признаков параллелограмма и трапеции
Применение теории паркета для доказательства свойств и признаков параллелограмма и трапеции Числовые ряды
Числовые ряды Текстовые задачи. Движение по кругу и по воде
Текстовые задачи. Движение по кругу и по воде Золотое сечение
Золотое сечение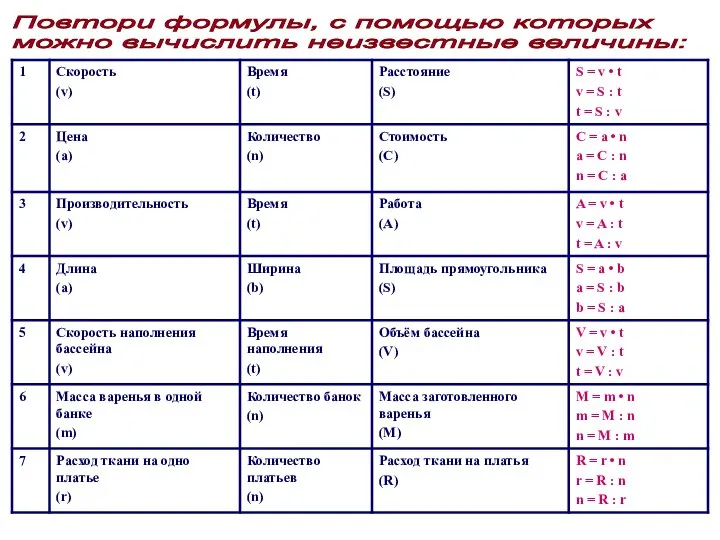 Скорость (v), Время (t), Расстояние (S)
Скорость (v), Время (t), Расстояние (S) Степенные ряды
Степенные ряды Задачи на проценты. Решения
Задачи на проценты. Решения