Содержание
- 2. Дифференциальным уравнением (ДУ) Решением ДУ является - называется уравнение, содержащее производные от искомой функции или её
- 3. 3 4 1 1 1
- 6. Пример 1. Найдите частное решение дифференциального уравнения , если y=2, при Решение: y=2 при x=
- 7. Пример 2. Скорость тела, выходящего из состояния покоя, равна Определите путь, пройденный телом за 3с. Т.
- 8. Пример 3. Найдите уравнение линии, проходящей через точку М(1;3) и имеющей касательную, угловой коэффициент которой равен
- 9. Пример 4. Скорость размножения некоторых бактерий пропорциональна их количеству в рассматриваемый момент времени t. Количество бактерий
- 10. Пример 4. Скорость размножения некоторых бактерий пропорциональна их количеству в рассматриваемый момент времени t. Количество бактерий
- 11. Пример 5. Скорость распада радия пропорциональна его количеству в данный момент времени. Найдите закон радиоактивного распада,
- 13. Скачать презентацию

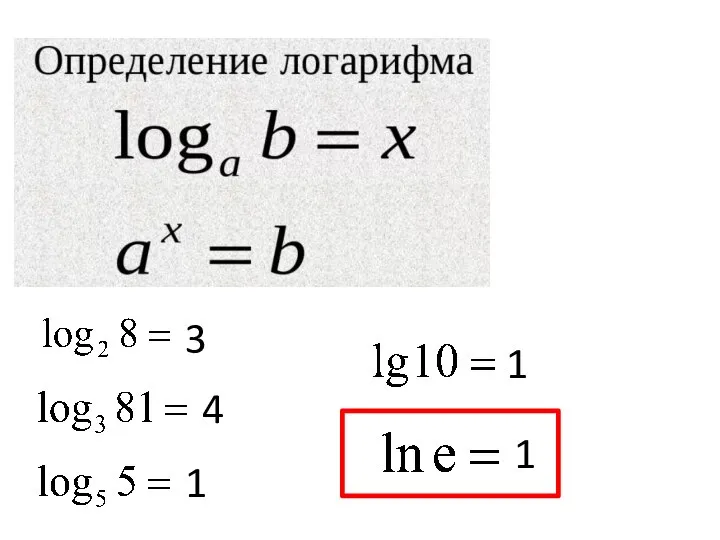
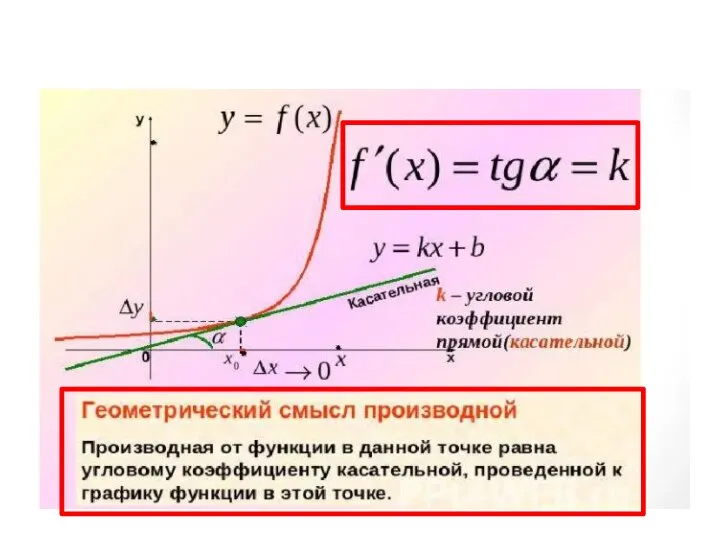







 Электронное пособие. Основные понятия и определения в математике
Электронное пособие. Основные понятия и определения в математике Рекурсивные алгоритмы
Рекурсивные алгоритмы Графики элементарных функций. Повторение
Графики элементарных функций. Повторение Движение. Его виды и применение. 9 класс
Движение. Его виды и применение. 9 класс Презентация на тему Использование графов в решении логических задач
Презентация на тему Использование графов в решении логических задач  Применение функциональных зависимостей в реальных процессах и явлениях
Применение функциональных зависимостей в реальных процессах и явлениях Графики. График движения
Графики. График движения Теорема о свойстве биссектрисы с доказательством
Теорема о свойстве биссектрисы с доказательством Иррациональные уравнения (часть 1)
Иррациональные уравнения (часть 1) Арктангенс и арккотангенс
Арктангенс и арккотангенс Множественные связи. Порядковые и категоризованные переменные
Множественные связи. Порядковые и категоризованные переменные Падпрасторы лінейнай прасторы
Падпрасторы лінейнай прасторы Решение задач
Решение задач Выражение (для печатной и электронной формы учебника)
Выражение (для печатной и электронной формы учебника) Геометрический диктант
Геометрический диктант Практическое применение площадей геометрических фигур
Практическое применение площадей геометрических фигур Неравенства (9 класс)
Неравенства (9 класс) Площадь фигуры. Сравнение площадей
Площадь фигуры. Сравнение площадей Спиннеры и метематика
Спиннеры и метематика Аксиомы стереометрии
Аксиомы стереометрии Математическая викторина В гостях у мудрой совы 2 класс
Математическая викторина В гостях у мудрой совы 2 класс Повторение изученного материала. 1 класс
Повторение изученного материала. 1 класс Организации проектной деятельности
Организации проектной деятельности Решение тригонометрических неравенств
Решение тригонометрических неравенств Презентация на тему Решение систем неравенств (8 класс)
Презентация на тему Решение систем неравенств (8 класс)  Решение задач по теме Параллельные прямые
Решение задач по теме Параллельные прямые Решение задач на применение признаков подобия
Решение задач на применение признаков подобия Признаки равенства треугольников. Задачи на готовых чертежах
Признаки равенства треугольников. Задачи на готовых чертежах