Множества

Множества
Множество – совокупность некоторых объектов, рассматриваемая как единое целое
a∈A
Г. Кантор
N, Z, Q, R
A ⊆ B
Свойства:
A – подмножество B, если множество A состоит из элементов, принадлежащих B
a∉A
N ⊆ Z ⊆ Q ⊆ R
1) A ⊆ A
2) Если A ⊆ B и B ⊆ A, то A = B
3) Если A ⊆ B и B ⊆ C, то A ⊆ C
∅ ⊆ A
|A| - мощность

Множества
Булеан множества P(A) – множество всех подмножеств множества A
Свойства:
A = {a,b,c}
1) A = A
2) Если A = B, то B = A
3) Если A = B и B = C, то A = C
Если |A|=n, то |P(A)|=
2n
P(A) = {
∅
, {a}, {b}, {c}
, {a,b}, {a,c}, {b,c}
, A
}
A = B
Множества A и B равны, если A и B состоят из одних и тех же элементов

Способы задания множества
A = {a, b, c, 2, 3}
1) Перечисление элементов:
A = { x | P(x) }
2) Обобщение 1 способа (закономерность):
K = {20, 21, 22, 23, …}
3) Характеристическим свойством:
A = { x∈R | x>0 }
4) С помощью операций над множествами (см. позже)
N, Z, Q, R
5) Стандартные обозначения:

Способы задания множества
Сегмент [a,b] =
6) Стандартные обозначения подмножеств множества R:
{ x∈R | a ≤ x ≤ b }
Интервал (a,b) =
{ x∈R | a < x < b }
Полусегмент [a,b) =
{ x∈R | a ≤ x < b }
Полуинтервал (a,b] =
{ x∈R | a < x ≤ b }

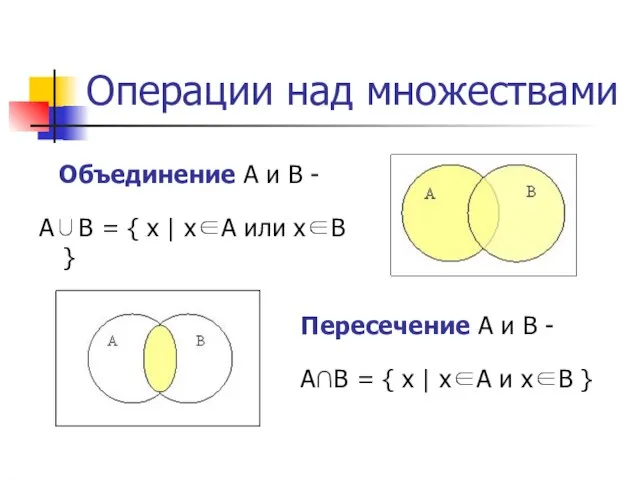
Операции над множествами
Объединение A и B -
A∪B = { x | x∈A или x∈B }
Пересечение A и B -
A∩B = { x | x∈A и x∈B }

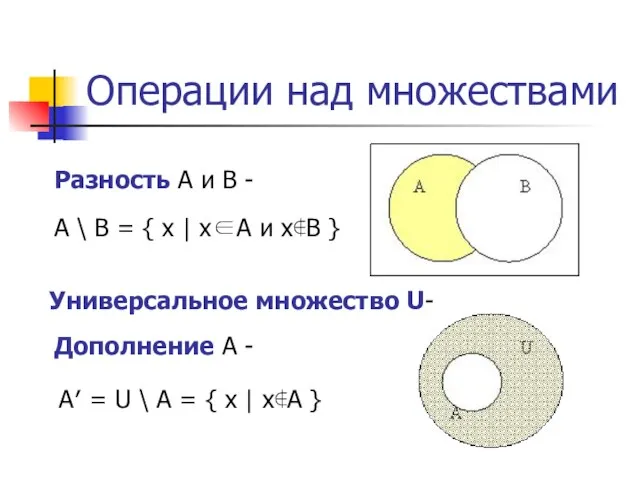
Операции над множествами
Разность A и B -
A \ B = { x | x∈A и x∉B }
Дополнение A -
A′ = U \ A =
Универсальное множество U-
{ x | x∉A }

Свойства операций
1. Ассоциативность:
4. Дистрибутивность:
(А∪B)∪C = A∪(B∪C)
(А∩B)∩C = A∩(B∩C)
2. Коммутативность:
А∪B = B∪A
А∩B = B∩A
3. А∪A = A,
А∩A = A
A∩(B∪C) = (A∩B)∪(A∩C)
A∪(B∩C) = (A∪B)∩(A∪C)
(А∪B)∩A = A,
(А∩B)∪A = A
5. Поглощение: