Возведение одночлена в степень

ЧТОБЫ ВОЗВЕСТИ СТЕПЕНЬ В СТЕПЕНЬ, НУЖНО ОСНОВАНИЕ ОСТАВИТЬ ТЕМ ЖЕ, А ПОКАЗАТЕЛИ СТЕПЕНЕЙ ПЕРЕМНОЖИТЬ.

(a5)4
=a5∙a5∙a5∙a5
=a5+5+5+5
=a20
Если a – произвольное число, m и n – любые натуральные числа, то:
(am)n=amn
n раз
n раз
(am)n
=am∙am∙…∙am
=am+m+…+m
=amn

(abc)n
=anbncn
(abcd)n
=anbncndn
ЧТОБЫ ВОЗВЕСТИ В СТЕПЕНЬ ПРОИЗВЕДЕНИЕ, НУЖНО ВОЗВЕСТИ В ЭТУ СТЕПЕНЬ КАЖДЫЙ МНОЖИТЕЛЬ И РЕЗУЛЬТАТЫ ПЕРЕМНОЖИТЬ.

(ab)4
=(ab)∙(ab)∙(ab)∙(ab)
=(a∙a∙a∙a)∙(b∙b∙b∙b)
=
=a4b4
Если a и b – произвольные числа и n – натуральное число, то:
(ab)n=anbn
(ab)n
=(ab)∙(ab)∙…∙(ab)
=(a∙a∙…∙a)∙(b∙b∙…∙b)
=anbn
n раз
n раз
n раз

n раз
a n
=
b
a
b
∙
a
b
∙…∙
a
b
=
an
bn
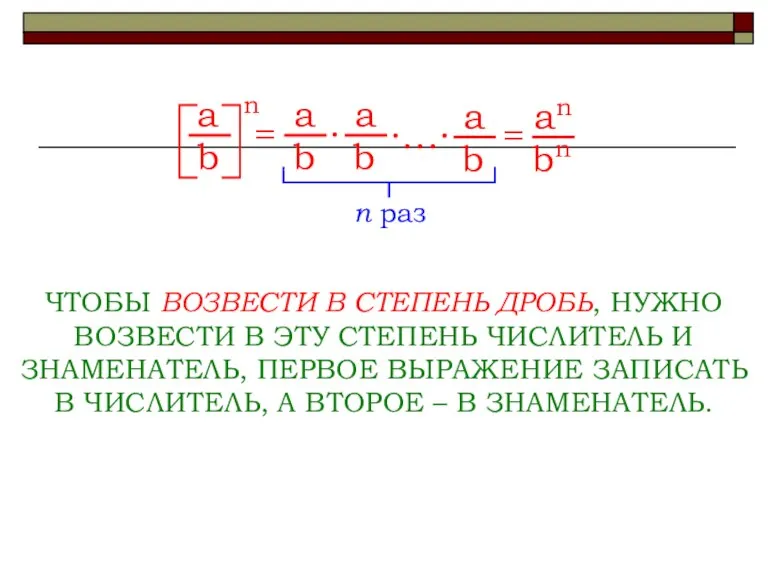
ЧТОБЫ ВОЗВЕСТИ В СТЕПЕНЬ ДРОБЬ, НУЖНО ВОЗВЕСТИ В ЭТУ СТЕПЕНЬ ЧИСЛИТЕЛЬ И ЗНАМЕНАТЕЛЬ, ПЕРВОЕ ВЫРАЖЕНИЕ ЗАПИСАТЬ В ЧИСЛИТЕЛЬ, А ВТОРОЕ – В ЗНАМЕНАТЕЛЬ.

(ab)n=anbn
(am)n=amn

Возведем одночлен -3a3b2 в шестую степень:
ПРИМЕР 1:
(-3a3b2)6
=(-3)6∙(a3)6∙(b2)6
=729a18b12

Возведем одночлен –x4y3z в третью степень:
ПРИМЕР 2:
(–x4y3z)3
=(-1)3∙(x4)3∙(y3)3∙z3
=-x12y9z3

Работа с учебником
Стр. 111
№ 473