парні і непарні функції-1

ПАРНІ І НЕПАРНІ ФУНКЦІЇ

Парні і непарні функції
Означення. Функцію f називають парною, якщо для будь-якого x з області визначення f (–x) = f (x).
Означення. Функцію f називають непарною, якщо для будь-якого x з області визначення f (–x) = –f (x).
Очевидно, що функція y = x2 є парною, а функція y = x3 — непарною.

Парні і непарні функції
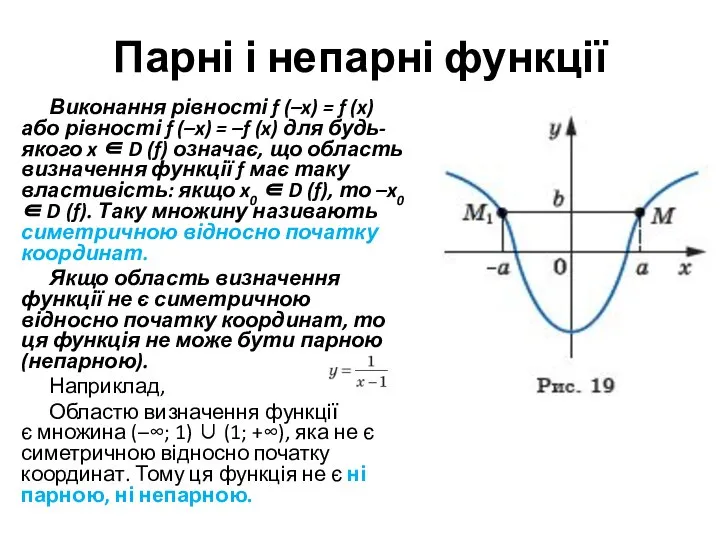
Виконання рівності f (–x) = f (x) або рівності f (–x) = –f (x) для будь-якого x ∈ D (f) означає, що область визначення функції f має таку властивість: якщо x0 ∈ D (f), то –x0 ∈ D (f). Таку множину називають симетричною відносно початку координат.
Якщо область визначення функції не є симетричною відносно початку координат, то ця функція не може бути парною (непарною).
Наприклад,
Областю визначення функції є множина (–∞; 1) ∪ (1; +∞), яка не є симетричною відносно початку координат. Тому ця функція не є ні парною, ні непарною.

Приклад 1
Доведіть, що функція f (x) = x3 – x є непарною.
Розв’язання.
Оскільки D (f) = R, то область визначення функції f симетрична відносно початку координат.
Для будь-якого x ∈ D (f) маємо f (–x) = (–x)3 – (–x) = –x3 + x = = –f (x).
Отже, функція f є непарною.

Приклад 2

Теорема 4.1
Вісь ординат є віссю симетрії графіка парної функції.
Доведення.
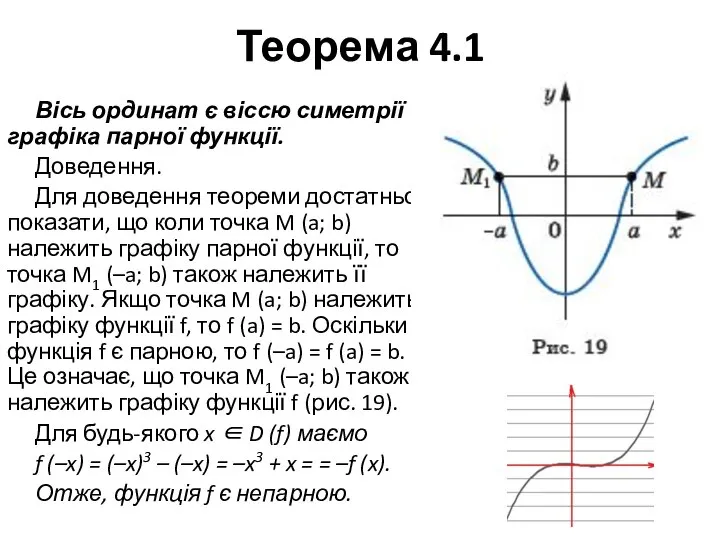
Для доведення теореми достатньо показати, що коли точка M (a; b) належить графіку парної функції, то точка M1 (–a; b) також належить її графіку. Якщо точка M (a; b) належить графіку функції f, то f (a) = b. Оскільки функція f є парною, то f (–a) = f (a) = b. Це означає, що точка M1 (–a; b) також належить графіку функції f (рис. 19).
Для будь-якого x ∈ D (f) маємо
f (–x) = (–x)3 – (–x) = –x3 + x = = –f (x).
Отже, функція f є непарною.

Теорема 4.2
Початок координат є центром симетрії графіка непарної функції.
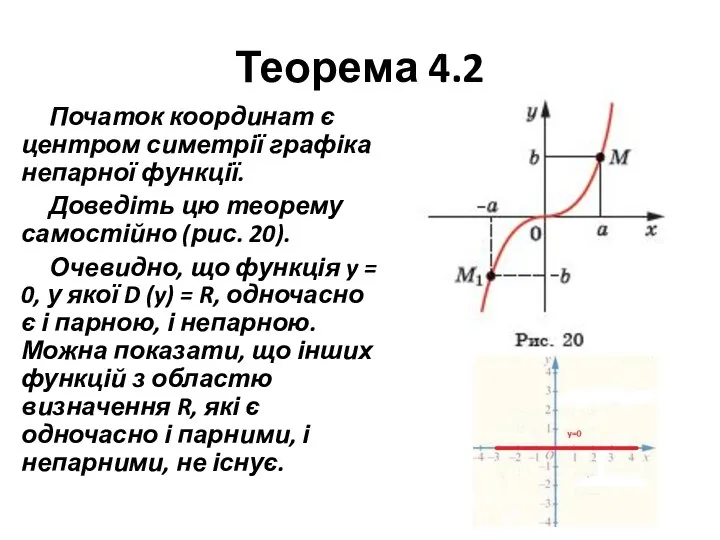
Доведіть цю теорему самостійно (рис. 20).
Очевидно, що функція y = 0, у якої D (y) = R, одночасно є і парною, і непарною. Можна показати, що інших функцій з областю визначення R, які є одночасно і парними, і непарними, не існує.

Первинне закріплення теоретичного матеріалу
Яку функцію називають парною?
Яку функцію називають непарною?
Яку множину називають симетричною відносно початку координат?
Сформулюйте властивість графіка парної функції.
Сформулюйте властивість графіка непарної функції.

Тренувальні вправи

Тренувальні вправи

Тренувальні вправи

Тренувальні вправи

Вправа для повторення