Содержание
- 2. Учебные материалы
- 3. Комбинаторика изучает число комбинаций из предметов Перестановки - важен только порядок. Пример. Сколькими способами можно расставить
- 4. Рассмотрим n занумерованных ячеек: Pn = n(n - 1)(n - 2)...⋅3⋅2⋅1=n! (факториал)
- 5. Размещения: определение, формулы для вычисления числа размещений (без возвращения/с возвращением), пример
- 6. -- важен порядок и состав. Пример. Всего 10 цифр. Сколькими способами можно составить трехзначный номер? Размещения
- 7. Формула выводится с помощью k ячеек
- 8. Размещения с повторениями. Все важно – и порядок, и предметы, причем их можно повторять.
- 9. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по каждой
- 11. Сочетания: определение, формулы для вычисления числа сочетаний , пример
- 12. Разные предметы, порядок не важен. Пример. В группе 20 человек. Сколькими способами можно выбрать трех делегатов
- 14. Создатели теории вероятностей
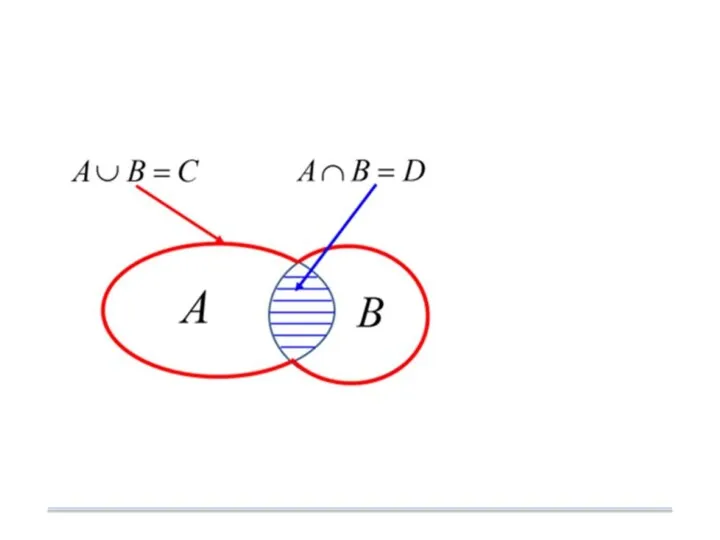
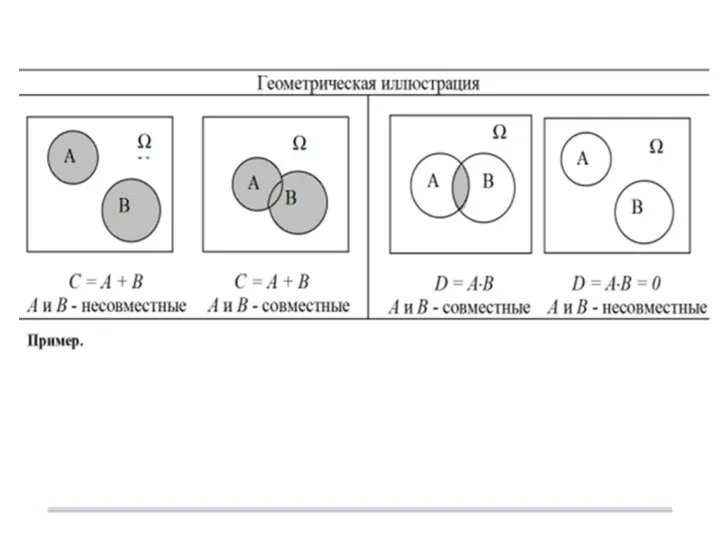
- 19. 5.2. Алгебра событий
- 26. Определение вероятности событий: классическое, геометрическое, статистическое
- 28. Примеры непосредственного вычисления вероятностей случайных событий Формула
- 29. Брошена игральная кость. Какова вероятность выпадения простого числа? Перечислим все простые числа от 1 до 6.
- 30. Брошен кубик два раза подряд. Какова вероятность, что оба раза выпадут четные числа? Событие --- выпали
- 31. Правило умножения Если комбинация состоит из вариантов, каждый вариант состоит из других вариантов то пара состоит
- 32. Вычислим , то есть перечислим пары
- 33. Монету бросали 3 раза. Найти вероятность того, что «решка» выпала 2 раза. Переберём все возможные исходы
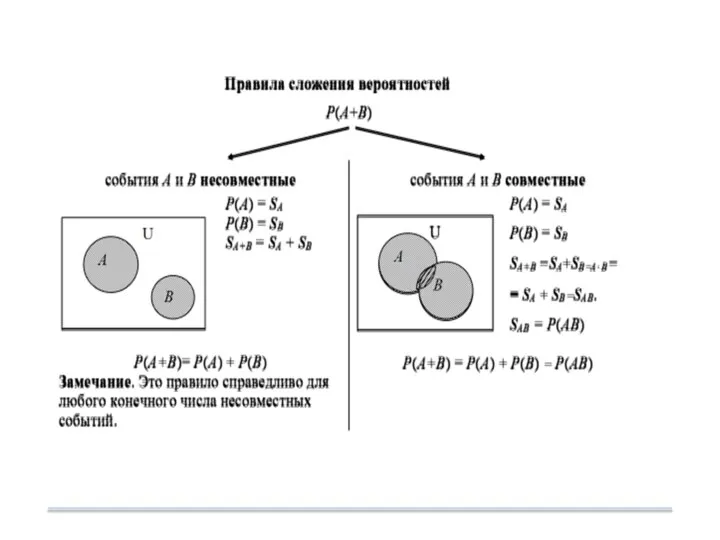
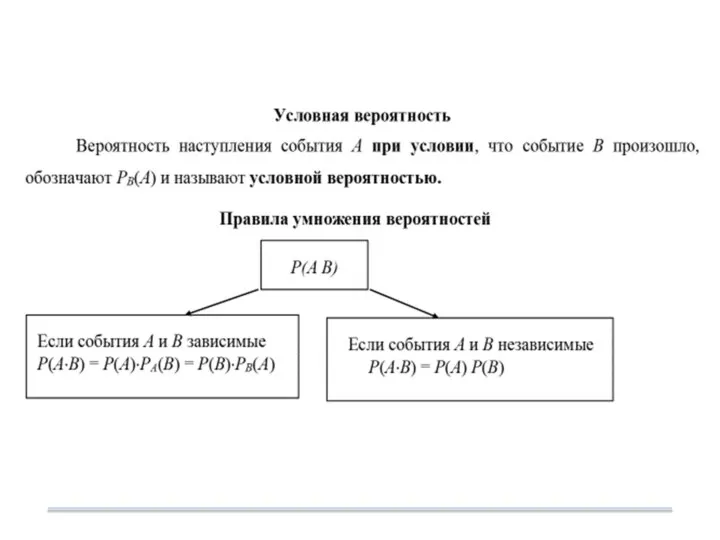
- 34. 5.3.Основные теоремы теории вероятностей
- 43. Повторные испытания Бернулли
- 50. ФОРМУЛА ПУАССОНА
- 53. Формула полной вероятности Пусть даны два события и причем является суммой новых событий:
- 55. Так как то получаем формулу, которая называется формулой полной вероятности
- 56. Пример. В группе спортсменов 5 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму: для
- 57. Введем событие --- спортсмен выполнит норму. Гипотезы: --- лыжник, --- велосипедист, --- бегун.
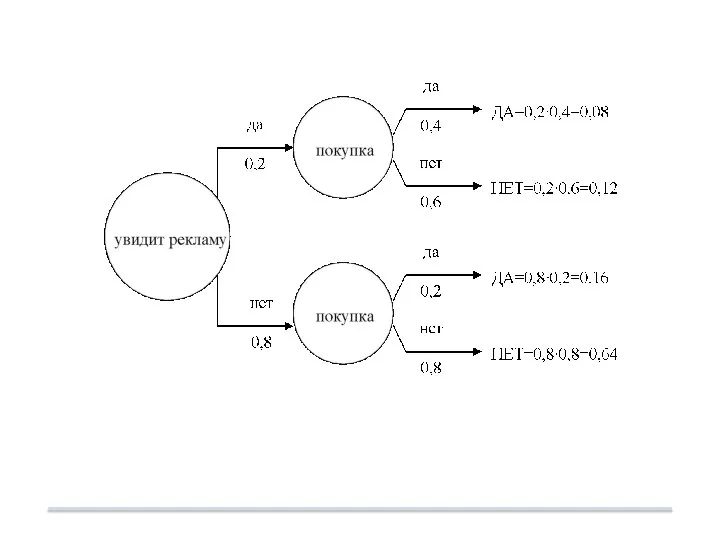
- 60. Вероятность того, что потребитель увидит рекламу некоторого товара, оценивается как 0,2. Вероятность покупки этого товара потребителем
- 61. Решение: используем так называемое «дерево вероятностей» В качестве отправной точки изобразим круг, обозначающий событие «увидит рекламу»
- 63. Двигаясь по каждой «ветке» слева направо, перемножим все вероятности, попадающиеся на пути, и запишем полученные значения
- 64. Если рассмотрение событий (гипотез) Н1, Н2,…, Нп позволяет делать какие-то заключения относительно события A, то естественно
- 65. Пример. Клиент звонит на сервисный номер с целью получить консультацию. Все звонки распределяются между тремя колл-центрами.
- 66. Решение: обозначим событие А – информация неточная, событие Hi – оператор относится к i-му колл-центру. Распишем
- 68. Скачать презентацию








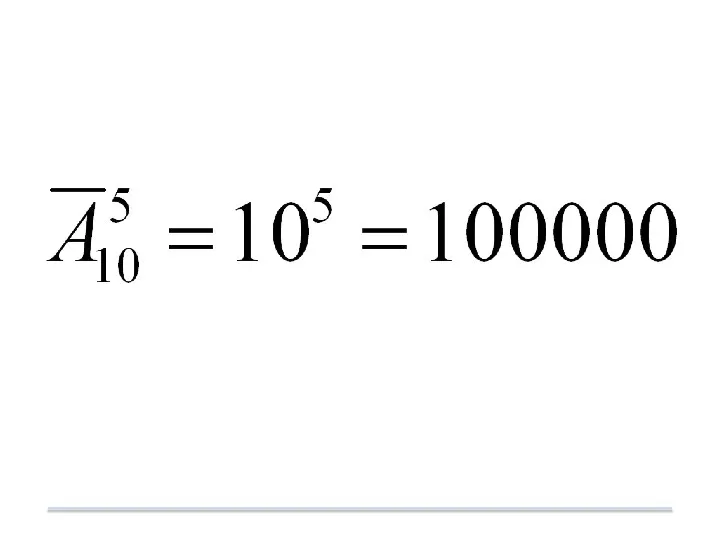


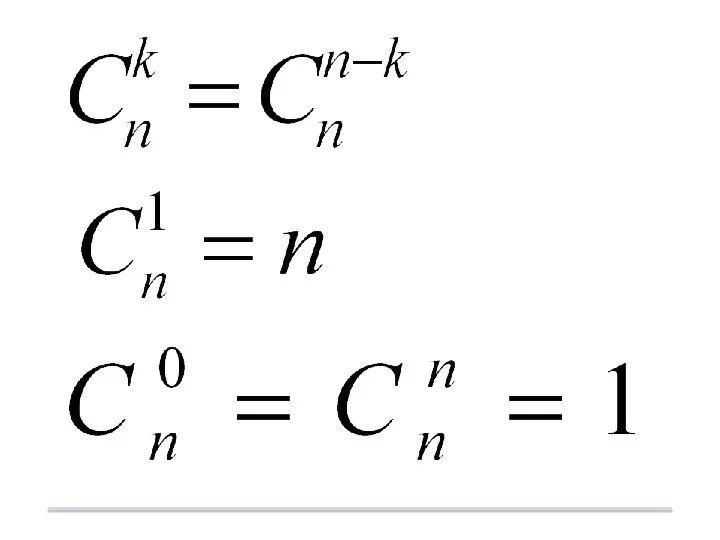








































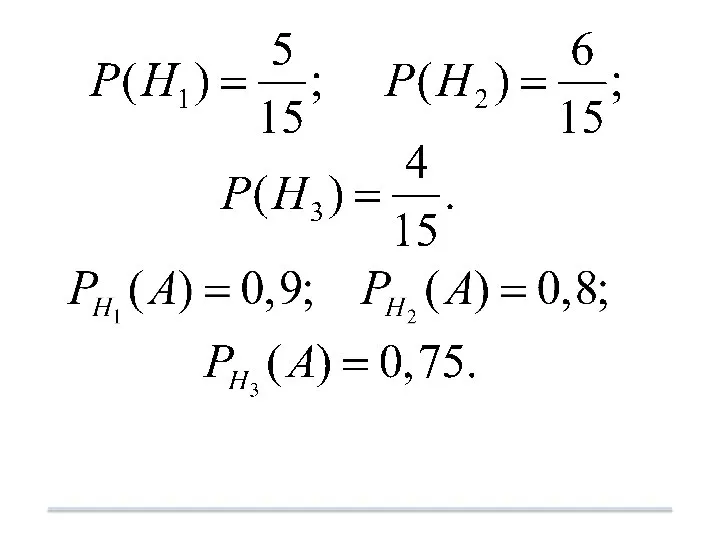
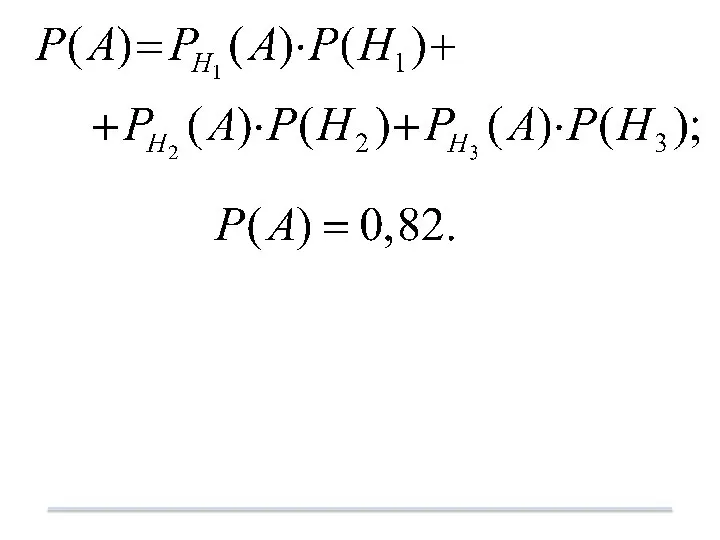






 Урок геометрии в 7 классе Искусство рассуждать
Урок геометрии в 7 классе Искусство рассуждать Проверочная работа
Проверочная работа Формулы двойного аргумента
Формулы двойного аргумента Функции и их графики
Функции и их графики Презентация на тему Занимательная математика (4 класс)
Презентация на тему Занимательная математика (4 класс)  Несобственные интегралы второго рода
Несобственные интегралы второго рода Числовая последовательность
Числовая последовательность Сигнальные карточки
Сигнальные карточки Презентация на тему Функция y=x2
Презентация на тему Функция y=x2  Площадь треугольника
Площадь треугольника Представление информации. Решение задач на проценты
Представление информации. Решение задач на проценты Рациональные уравнения
Рациональные уравнения Рене Декарт (1596 -1650)
Рене Декарт (1596 -1650) Математика. Задачи
Математика. Задачи На лесной поляне
На лесной поляне Поверхности второго порядка
Поверхности второго порядка Признаки равенства треугольников
Признаки равенства треугольников Экономический факторный анализ. Теорема о среднем
Экономический факторный анализ. Теорема о среднем Метод резолюций в алгебре высказываний
Метод резолюций в алгебре высказываний Ломаная линия. Обозначение ломаной
Ломаная линия. Обозначение ломаной Элементы круга и окружности в задачах ОГЭ
Элементы круга и окружности в задачах ОГЭ Начальные геометрические сведения. Признаки равенства треугольников
Начальные геометрические сведения. Признаки равенства треугольников Состав 12 и 11. Карточки
Состав 12 и 11. Карточки Шаблон презентации по математике
Шаблон презентации по математике Иррациональные уравнения
Иррациональные уравнения Презентация на тему Объём многогранника
Презентация на тему Объём многогранника  Составление текстовых задач по математике , связанные с историей, литературой, географией и др
Составление текстовых задач по математике , связанные с историей, литературой, географией и др Эта загадочная Бутылка Клейна
Эта загадочная Бутылка Клейна