Содержание
- 2. Растеризация — это перевод изображения, описанного векторным форматом в пиксели или точки, для вывода на дисплей
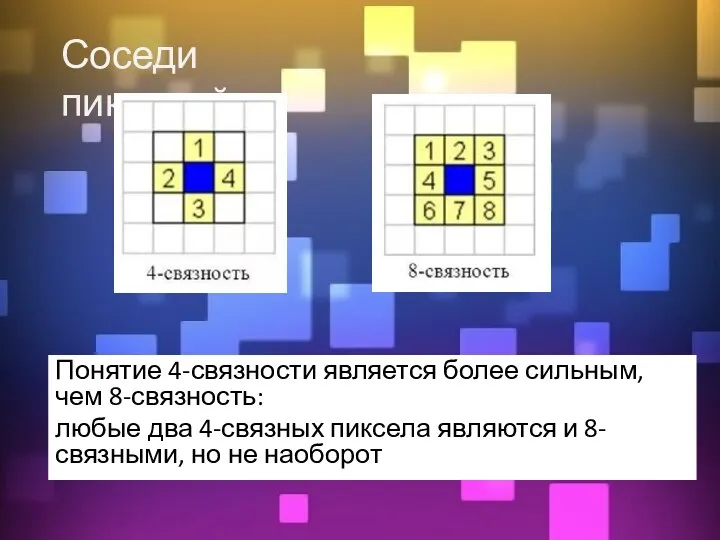
- 3. Понятие связности
- 4. Понятие 4-связности является более сильным, чем 8-связность: любые два 4-связных пиксела являются и 8-связными, но не
- 7. Простейший алгоритм растрового представления отрезка // File Line1.cpp void Line ( int x1, int y1, int
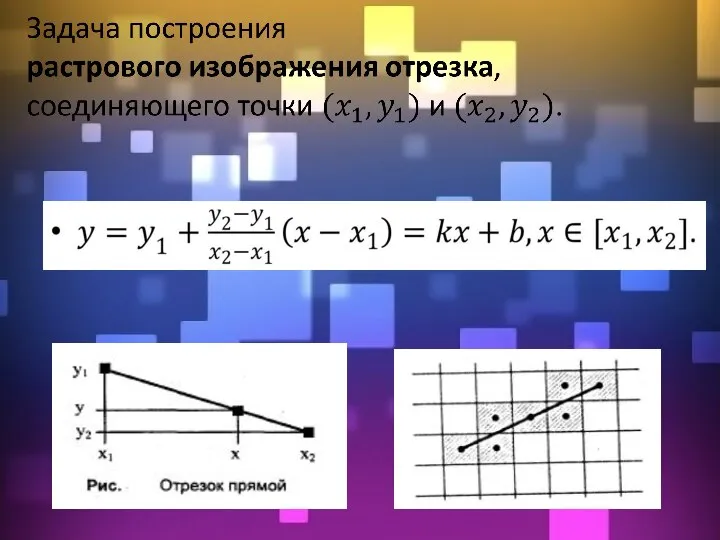
- 8. Процесс определения пикселов, наилучшим образом аппроксимирующих заданный отрезок, называется разложением в растр.
- 9. В 1965 году Брезенхейм предложил простой целочисленный алгоритм для растрового построения отрезка, первоначально предназначенный для использования
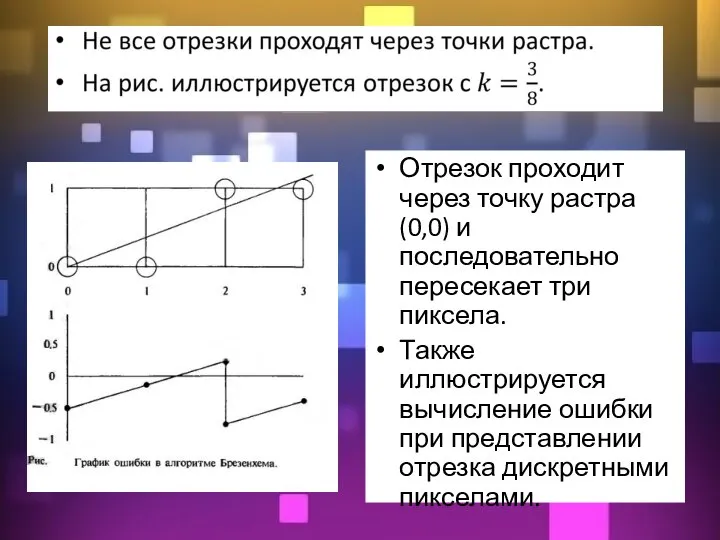
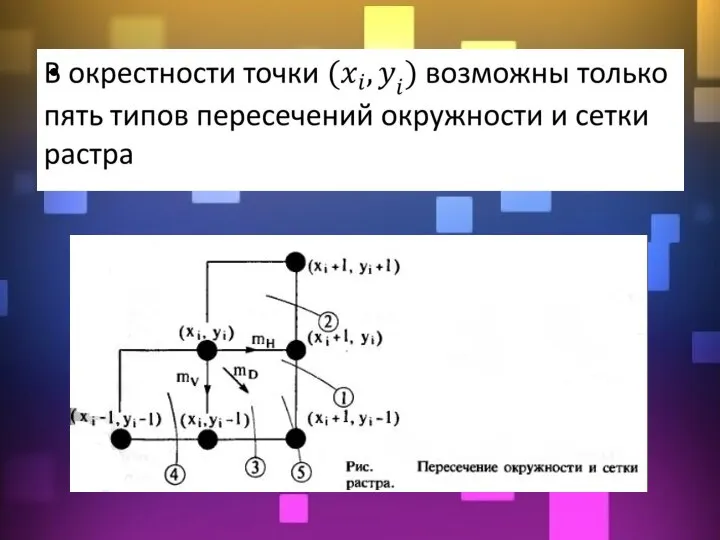
- 11. Отрезок проходит через точку растра (0,0) и последовательно пересекает три пиксела. Также иллюстрируется вычисление ошибки при
- 12. Алгоритмы построения отрезка имеют ряд недостатков: 1. выполняют операции над числами с плавающей точкой, а желательно
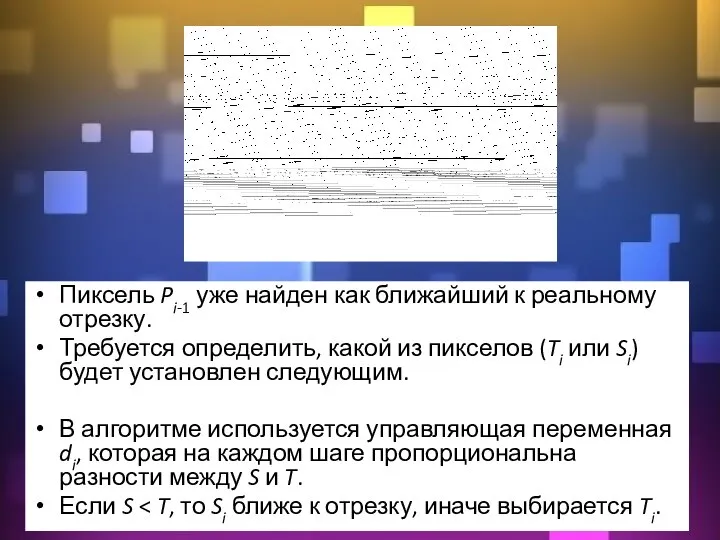
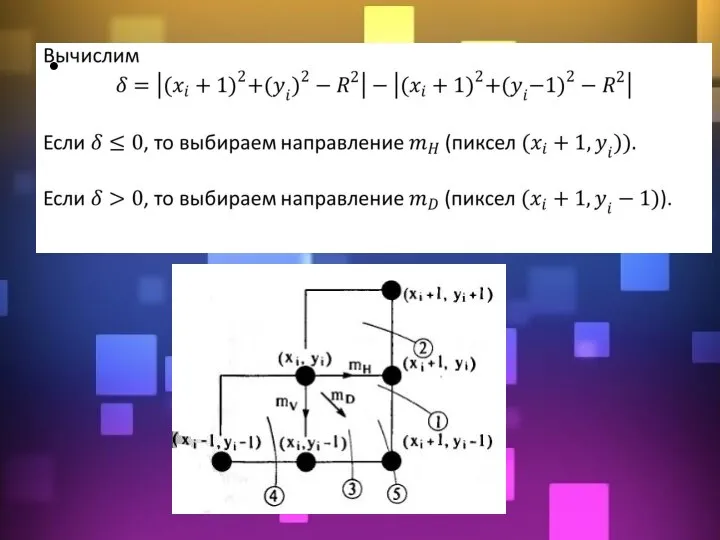
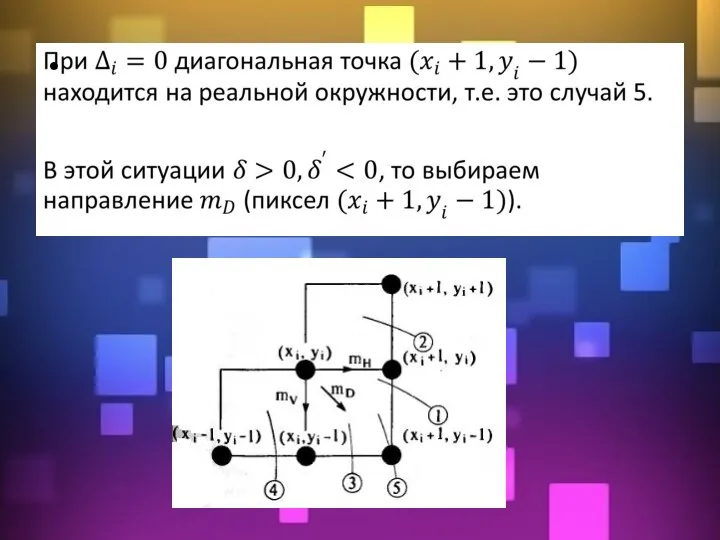
- 13. Пиксель Pi-1 уже найден как ближайший к реальному отрезку. Требуется определить, какой из пикселов (Ti или
- 14. Пусть отрезок проходит из точки (x1, y1) в точку (x2, y2). Исходя из начальных условий, точка
- 16. di = 2 xi-1 dy –2 yi-1 dx + 2 dy – dx. di+1 = 2
- 17. Если di ≥ 0, тогда выбирается Ti и yi = yi–1 + 1, di+1 = di
- 18. void MyLine(int x1, int y1, int x2, int y2, int c) { int dx, dy, inc1,
- 19. Методы устранения ступенчатости Основная причина появления лестничного эффекта заключается в том, что отрезки, ребра многоугольника, цветовые
- 20. Метод увеличения частоты выборки Каждый пиксель делится на подпиксели в процессе формирования растра более высокого разрешения.
- 21. Метод, основанный на использовании полутонов Интенсивность пикселя на ребре устанавливается пропорционально площади части пикселя, находящегося внутри
- 22. Растровое представление окружности
- 31. Окружность в I октанте сгенерирована. II октант получается зеркальным отражением относительно прямой y=x. Получаем I квадрант.
- 32. Двумерные матрицы соответствующих преобразований
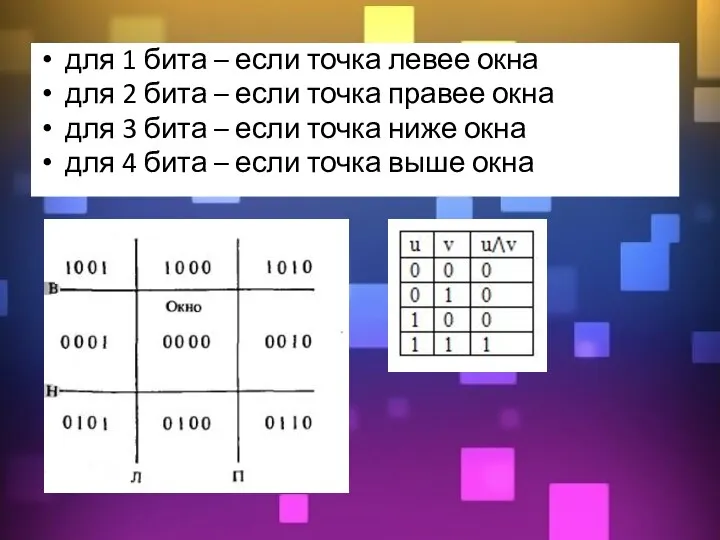
- 33. Отсечение отрезка. Алгоритм Сазерленда'Кохена Цель алгоритма: определение тех точек отрезка, которые лежат внутри отсекающего окна.
- 34. Отрезок называется видимым (лежащим внутри окна), если обе его концевые точки лежат внутри окна, например, отрезок
- 35. для 1 бита – если точка левее окна для 2 бита – если точка правее окна
- 38. Скачать презентацию



























 Нелинейное программирование
Нелинейное программирование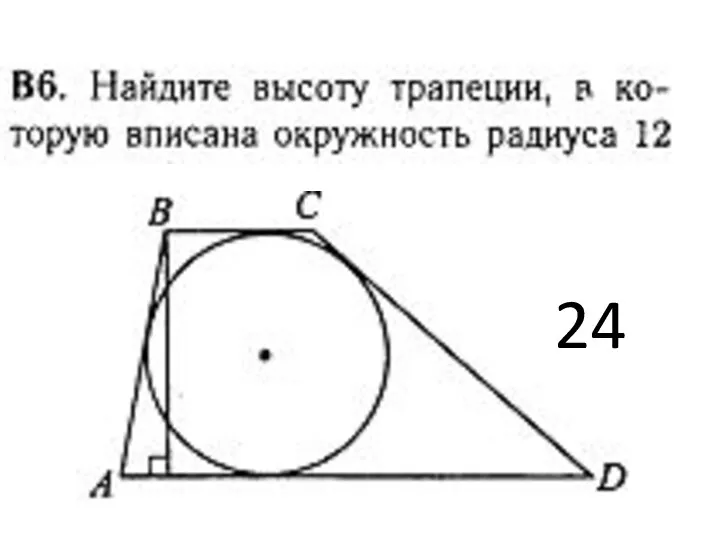 Задачи по геометрии
Задачи по геометрии Декартово произведение множеств. Лекция №5
Декартово произведение множеств. Лекция №5 Алгебраический способ решения задач
Алгебраический способ решения задач Упрощение выражений. Решение уравнений
Упрощение выражений. Решение уравнений Математика в профессии повара
Математика в профессии повара Презентация на тему Математическая сказка "Гуси лебеди" 3 класс
Презентация на тему Математическая сказка "Гуси лебеди" 3 класс  Интерактивная дидактическая игра Состав чисел до 10. Математика, 1 класс
Интерактивная дидактическая игра Состав чисел до 10. Математика, 1 класс Применение интеграла к вычислению площадей
Применение интеграла к вычислению площадей Лекции 19. Алгоритмы Маркова
Лекции 19. Алгоритмы Маркова Построение и анализ параллельных алгоритмов
Построение и анализ параллельных алгоритмов Внетабличное умножение и деление. Устный счёт
Внетабличное умножение и деление. Устный счёт Проценты. Примеры цепочкой
Проценты. Примеры цепочкой Презентация на тему Средняя линия треугольника (8 класс)
Презентация на тему Средняя линия треугольника (8 класс)  Решение задач на прямую и обратную пропорциональность
Решение задач на прямую и обратную пропорциональность Цифра 1. Посчитаем до 10
Цифра 1. Посчитаем до 10 Решите примеры
Решите примеры Презентация на тему Внетабличное умножение и деление
Презентация на тему Внетабличное умножение и деление  Графики в ОГЭ
Графики в ОГЭ Тела вращения. Урок 142
Тела вращения. Урок 142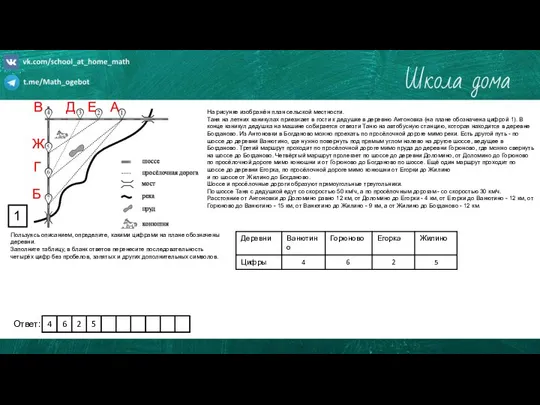 Практико-ориентированное задание
Практико-ориентированное задание Обыкновенные дроби
Обыкновенные дроби pril
pril Матрицы и действия над ними
Матрицы и действия над ними Решение систем с неизвестными множествами
Решение систем с неизвестными множествами Геометрическая прогрессия в экономике
Геометрическая прогрессия в экономике Помоги Незнайке выполнить задание от Знайки
Помоги Незнайке выполнить задание от Знайки Деление
Деление