Теория пределов. Понятие предела. Предел функции в точке. Теоремы о пределах. Замечательные пределы. Бесконечно малые функции

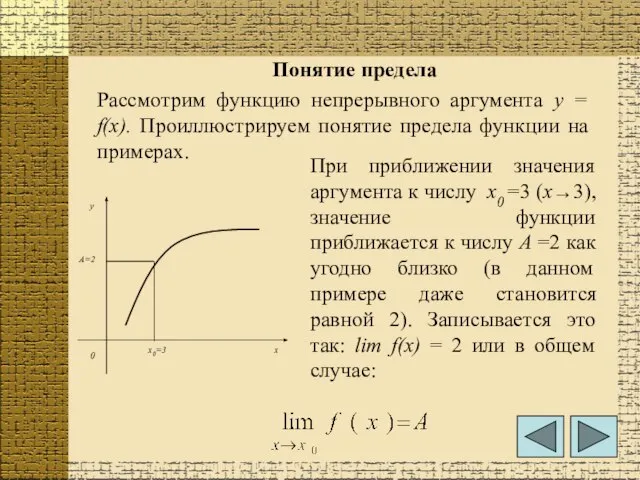
Понятие предела
Рассмотрим функцию непрерывного аргумента у = f(х). Проиллюстрируем понятие предела функции на примерах.
При приближении значения аргумента к числу х0 =3 (х→3), значение функции приближается к числу А =2 как угодно близко (в данном примере даже становится равной 2). Записывается это так: lim f(х) = 2 или в общем случае:

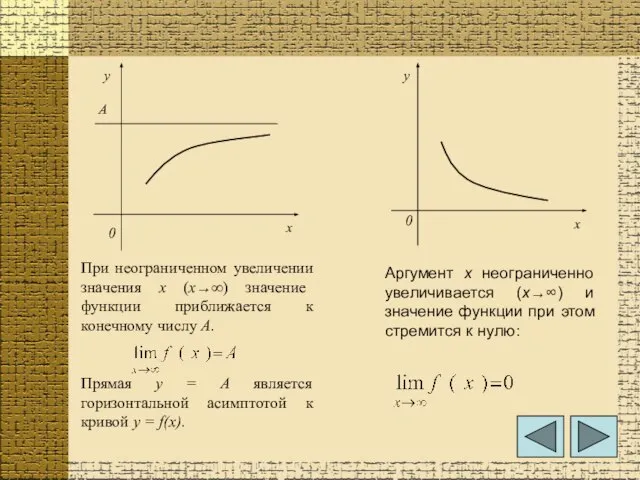
При неограниченном увеличении значения х (х→∞) значение функции приближается к конечному числу А.
Прямая у = А является горизонтальной асимптотой к кривой у = f(х).
Аргумент х неограниченно увеличивается (х→∞) и значение функции при этом стремится к нулю:

Теоремы о пределах
Теорема 1. Предел суммы функций f(х) и g(х)
при х→ + ∞ равен сумме их пределов:
Теорема 2. Предел произведения функций f(х) и g(х)
при х→ + ∞ равен произведению их пределов:
Следствие. Постоянный множитель можно выносить за знак предела:

Теорема 3. Если предел знаменателя g(х) при х→ + ∞ отличен от нуля, то предел дроби при х→ + ∞ равен отношению пределов числителя и знаменателя:
Предел функции в точке
Число b называется пределом функции f(x) при х → а, если разность f(x) – b , бесконечно малая функция при
х → а. Пишут

Пример 1. Вычислим
Решение:
Пример 2. Вычислим

Раскрытие неопределенностей вида
Рассмотрим предел
Вывод: если числитель дроби при х = а отличен от нуля, а ее знаменатель при х = а обращается в ноль, то предел при х = а не существует или равен ∞.

Пример 3. Вычислим
Решение:
Замечание ах2 + bx + c = a(x – x1)(x – x2);
a2 – b2 = (a – b)(a + b).

Пример 4. Вычислим
Решение:
(a-b)(a+b)=a2-b2

Пример 5. Вычислим
Пример 6. Вычислим
0 0
0 0

Пример 7. Вычислим
0 0
0 0 0

Пример 8. Вычислим

Вообще справедлива следующая теорема:
Теорема 4. Если числитель и знаменатель алгебраической дроби имеют одинаковые степени, то предел этой дроби при х⭢ + ∞ равен отношению коэффициентов при старших членах:
,
где ап ≠ 0, bn ≠ 0.

Если же степень числителя меньше степени знаменателя, то дробь бесконечно мала при х→+∞, т.е. ее предел равен нулю.
Наконец, если степень числителя больше степени знаменателя, то в этом случае предела нет, но говорят, что дробь стремится к бесконечности при х→+∞, и пишут

Первый и второй замечательные пределы
Большое практическое приложение имеют следующие пределы:
1-ый замечательный предел:
2-й замечательный предел:
1-я форма 2-я форма
е=2,72

Пример 1. Вычислим

Пример 2. Вычислим

Пример 3. Вычислим
Пример 4. Вычислим

Пример 5. Вычислим

Пример 6. Вычислим

Пример 7. Вычислим