Предел_посл_1

/24
V. Khudenko

§ 1 Числовая последовательность и ее предел
Числовой последовательностью называется функция натурального аргумента.
Обозначение:
Число x(n) называется общим членом последовательности, а формула
называется формулой общего члена последовательности .
V. Khudenko

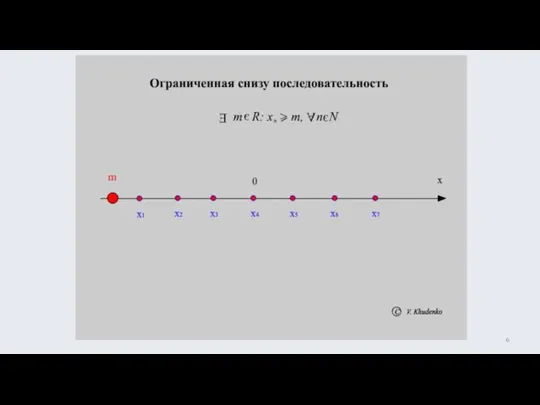
ограничена снизу на N

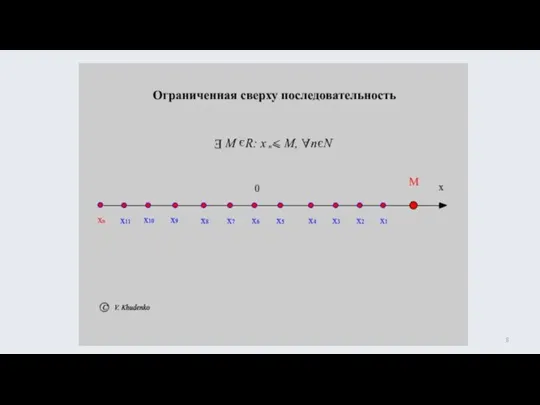
ограничена сверху на N

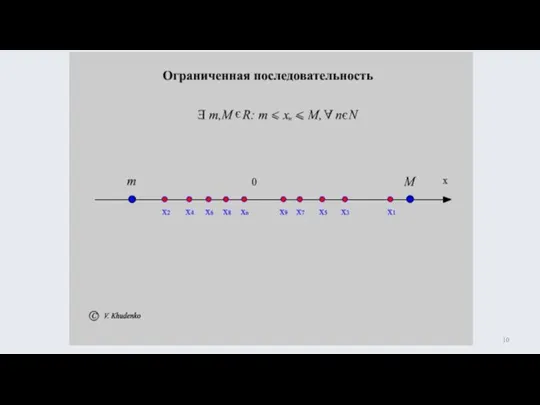
ограничена на N

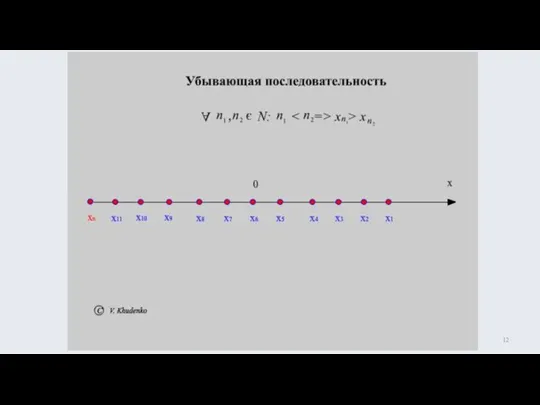
убывает на N
/24

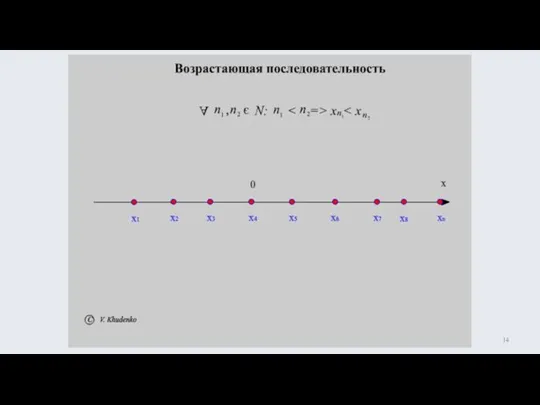
- возрастает на N
/24

Убывающие и возрастающие последовательности называются монотонными
Предел числовой последовательности
Понятие предела является одним из фундаментальных в математике. На этом понятии, как на фундаменте строится здание математического анализа.
V. Khudenko

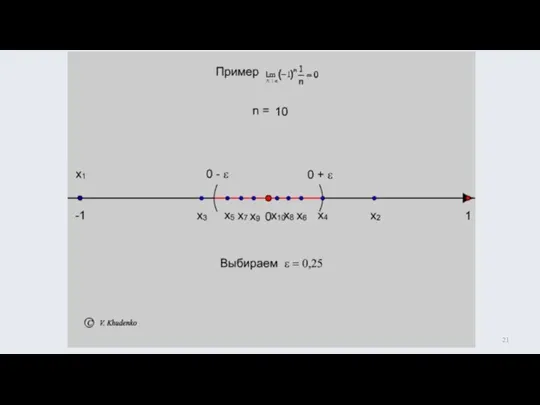
Число а называется пределом числовой последовательности , если для любого, сколь угодно малого положительного числа ε найдется такое натуральное число ,
что для всех члены этой последовательности удовлетворяют неравенству
В этом случае говорят, что последовательность имеет предел и пишут
V. Khudenko

Последовательность, имеющую предел называют сходящейся.
Эквивалентное определение
Число а называется пределом числовой последовательности , если в любой сколь угодно малой ε - окрестности числа а
содержатся все члены этой последовательности, начиная с некоторого числа
V. Khudenko

Свойства пределов последовательностей
Теорема 1. Если последовательность сходится, то она ограничена
Пусть - сходящаяся последовательность.
По определению предела последовательности существует натуральное число ,
что для любого выполняется неравенство Тогда для имеет место неравенство:
т.е.

Пусть
Тогда что и означает ограниченность числовой последовательности
Это только необходимый признак, например последовательность
ограниченная, но не сходящаяся.
Теорема 1.2. Если последовательность имеет предел, то только один.
Предположим, что
V. Khudenko

Пусть для определенности a
0 такое, что
Рассмотрим ε окрестности точек а и b . По выбору произвольного числа ε эти окрестности не пересекаются
Из того факта, что точка а является пределом последовательности следует, что все члены последовательности (за исключением конечного их числа) содержатся в ε окрестности этой точки.
V. Khudenko

Так как окрестности не пересекаются, то в ε окрестности точки b содержатся только конечное число членов последовательности.
Получаем противоречие с предположением, что .
Данное противоречие доказывает теорему.
Если встречается такая неограниченная последовательность, что с возрастанием n члены последовательности неограниченно возрастают, то такие последовательности называются бесконечно большими
V. Khudenko

V. Khudenko

V. Khudenko

V. Khudenko

Числовую последовательность называют бесконечно малой если ее предел равен нулю.
V. Khudenko

Свойства бесконечно малых и бесконечно больших последовательностей
Терема 1.3. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.
(1.1)
(1.2)
выполняется (*)
(**)
V. Khudenko

Обозначим возьмем
тогда неравенства (*) и (**) будут выполняться одновременно.
Мы получили, что для ∀ε>0 существует натуральное число n*, что для всех n>n*
Выполняется неравенство
следовательно, последовательность
является бесконечно малой.
V. Khudenko

Теорема 1.4. Произведение бесконечно малой последовательности на ограниченную является бесконечно малой.
Пусть (1.3)
и M>0
По определению предела последовательности
для
V. Khudenko

Следствие. Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема 1.5. Равносильны следующие два утверждения:
1)Обратная к бесконечно малой последовательности является бесконечно большой последовательностью;
2) Обратная к бесконечно большой последовательности является бесконечно малой последовательностью
V. Khudenko

1).Пусть , тогда
По свойствам числовых неравенств получаем, что для
т.е последовательность удовлетворяет определению бесконечно большой последовательности.
2) Пусть , следовательно,
по свойствам числовых неравенств
- бесконечно малая
V. Khudenko

Предел и неравенства
Теорема 1.5. Пусть и две сходящиеся последовательности
причем
тогда
Выберем тогда ε окрестности точек а и не будут пересекаться.
V. Khudenko