Прямой круговой конус

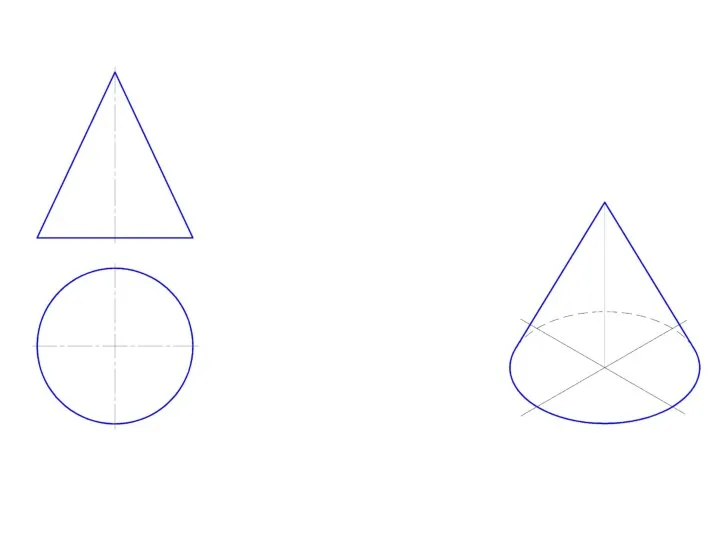
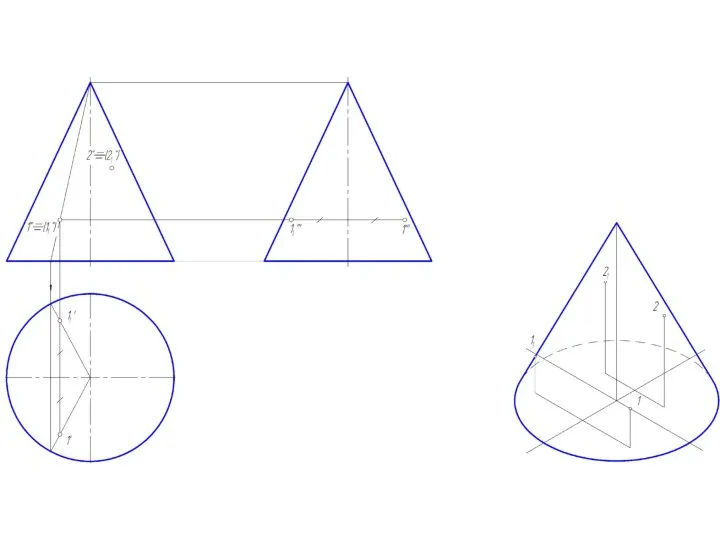
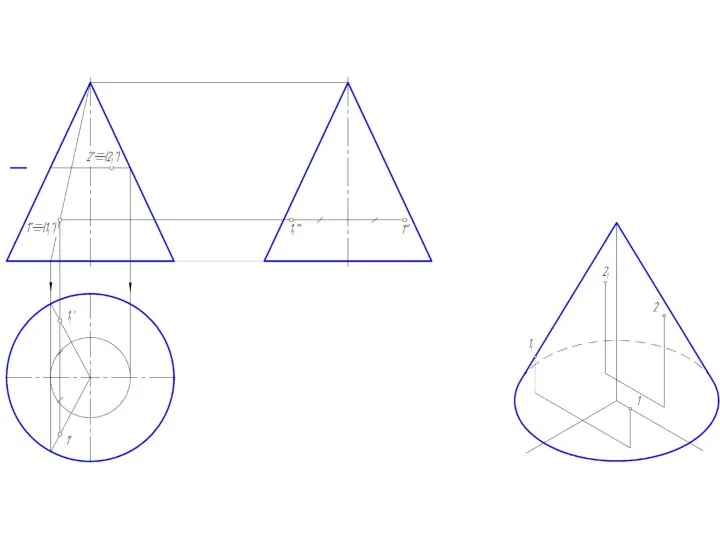
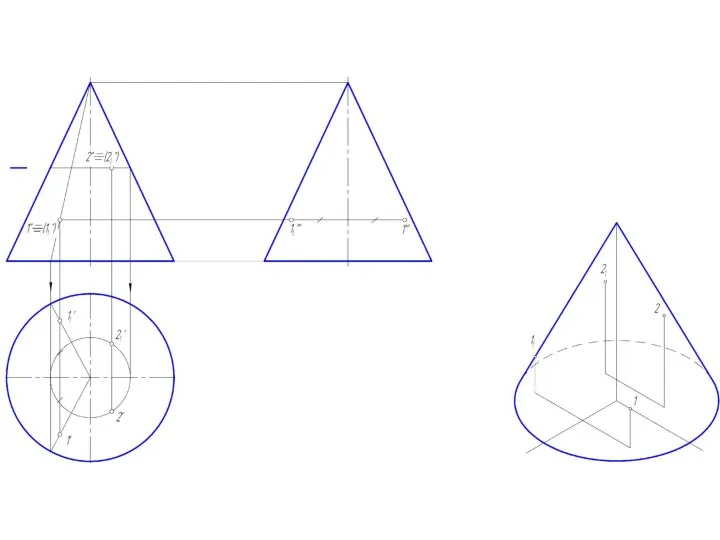
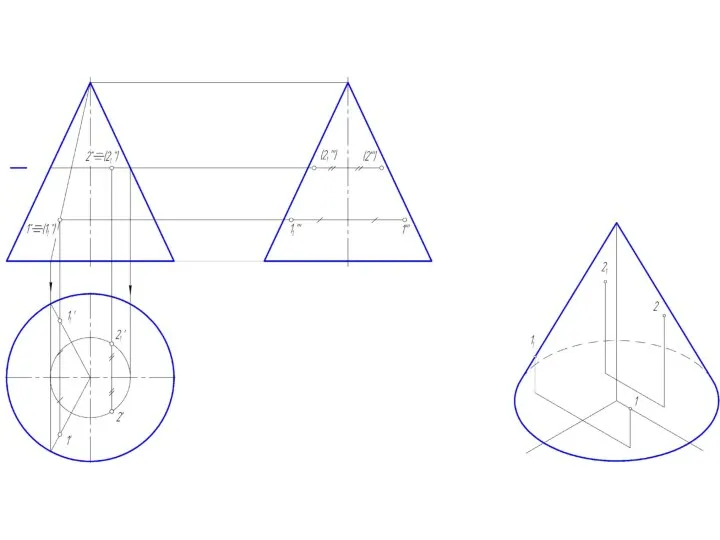
Точка на поверхности прямого кругового конуса
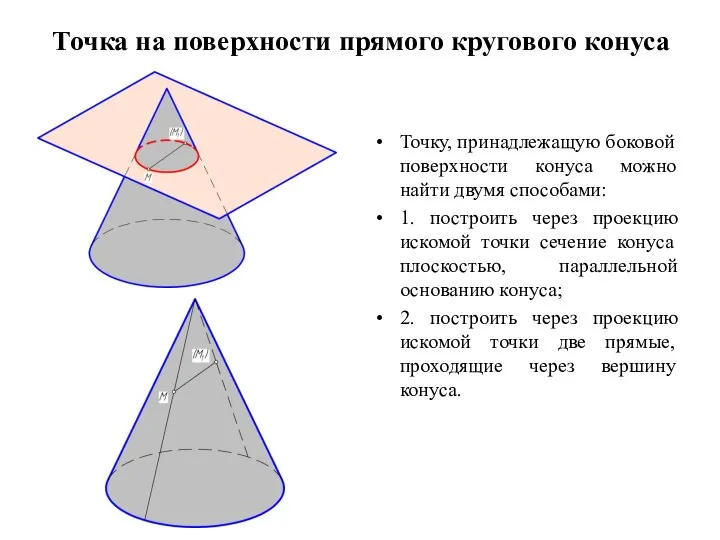
Точку, принадлежащую боковой поверхности конуса можно найти двумя способами:
1. построить через проекцию искомой точки сечение конуса плоскостью, параллельной основанию конуса;
2. построить через проекцию искомой точки две прямые, проходящие через вершину конуса.

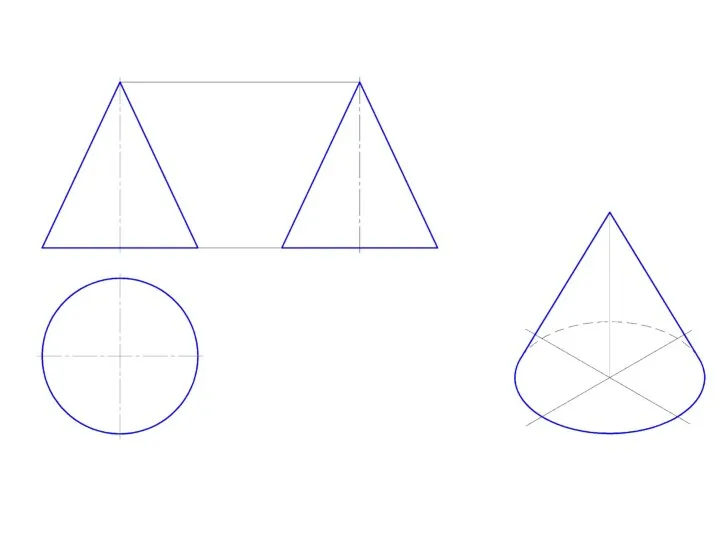
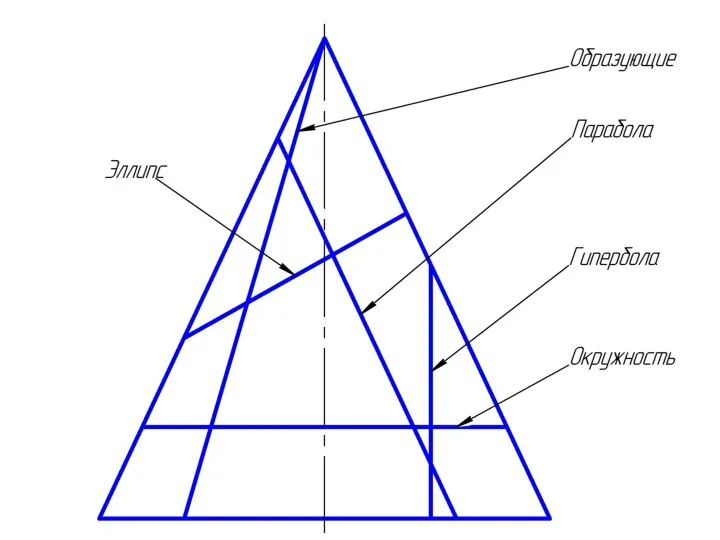
Пересечение прямого кругового конуса плоскостью
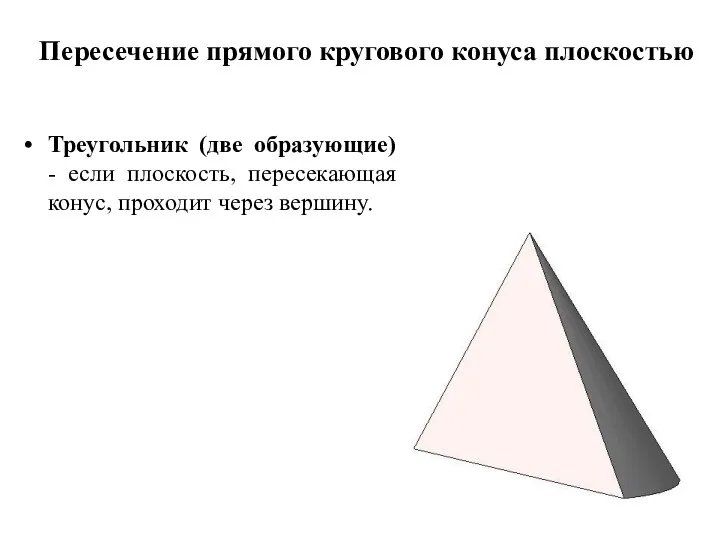
Треугольник (две образующие) - если плоскость, пересекающая конус, проходит через вершину.

Если конус пересекается плоскостью, не проходящей через его вершину, то в пересечении получается одна из следующих четырех кривых:
окружность – если секущая плоскость перпендикулярна оси конуса;
эллипс – если секущая плоскость пересекает все образующие
(не параллельна ни одной из образующих конуса);
парабола – если секущая плоскость параллельна только одной из образующих;
гипербола – секущая плоскость параллельна двум образующим.

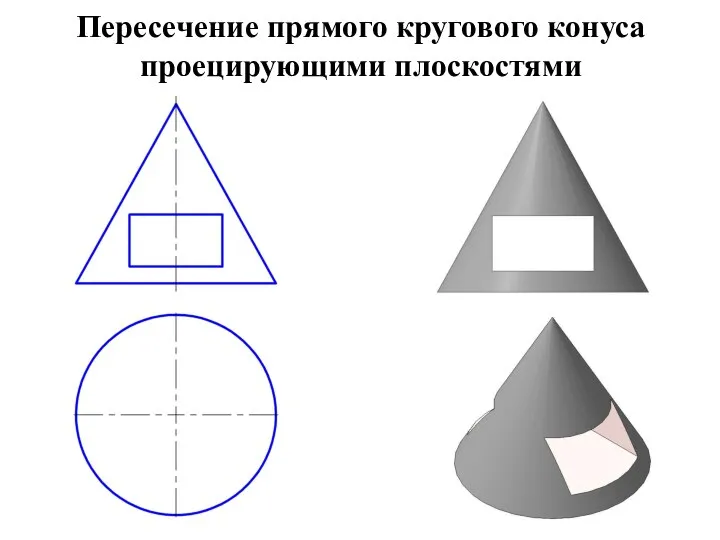
Пересечение прямого кругового конуса проецирующими плоскостями

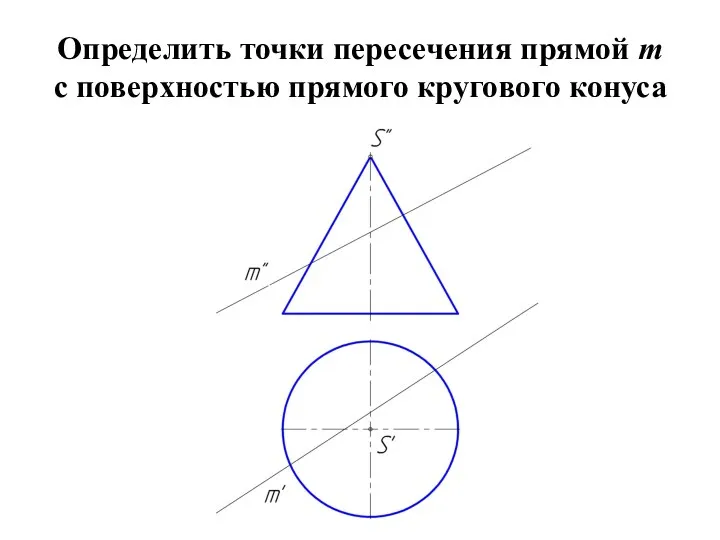
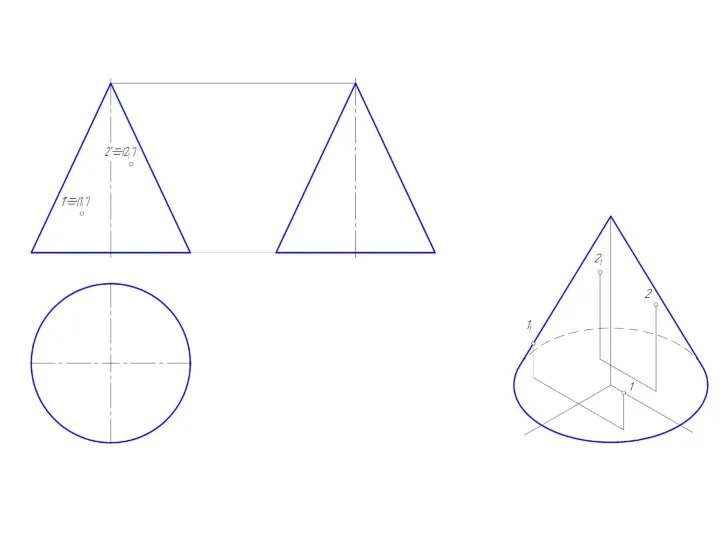
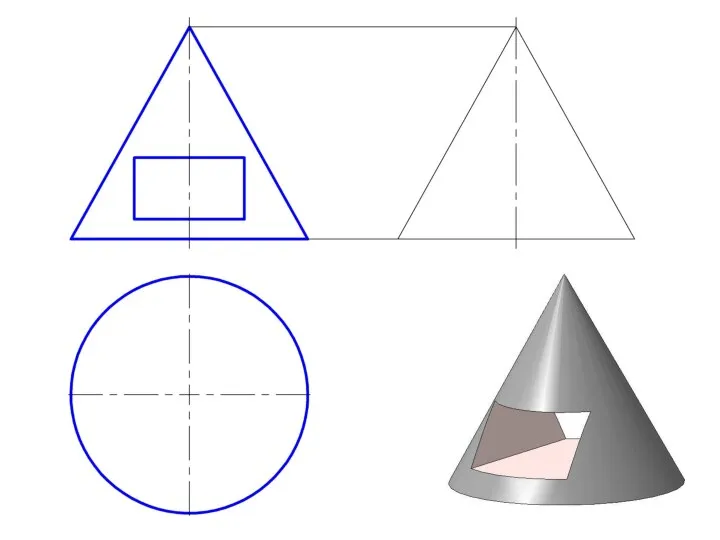
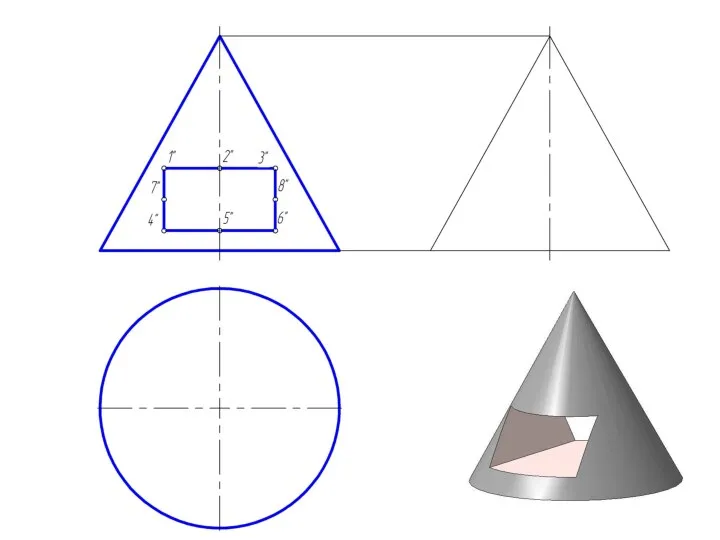
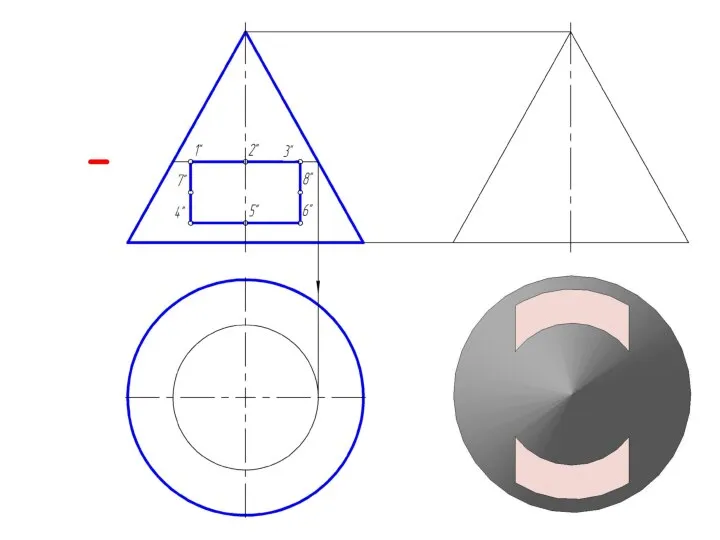
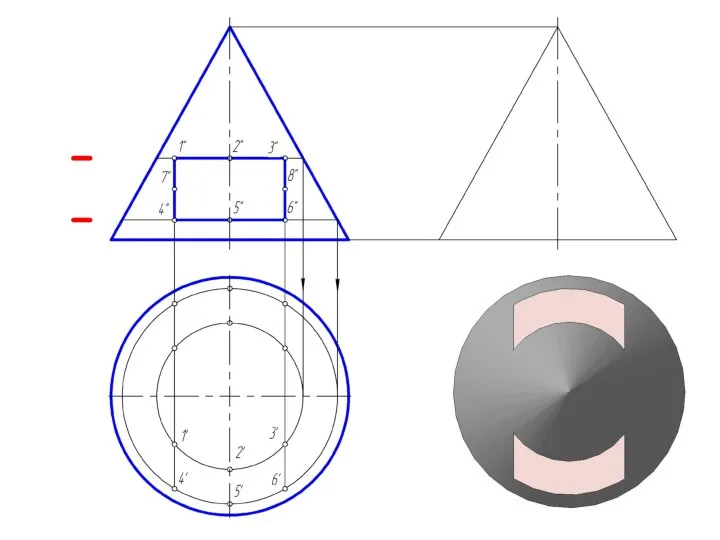
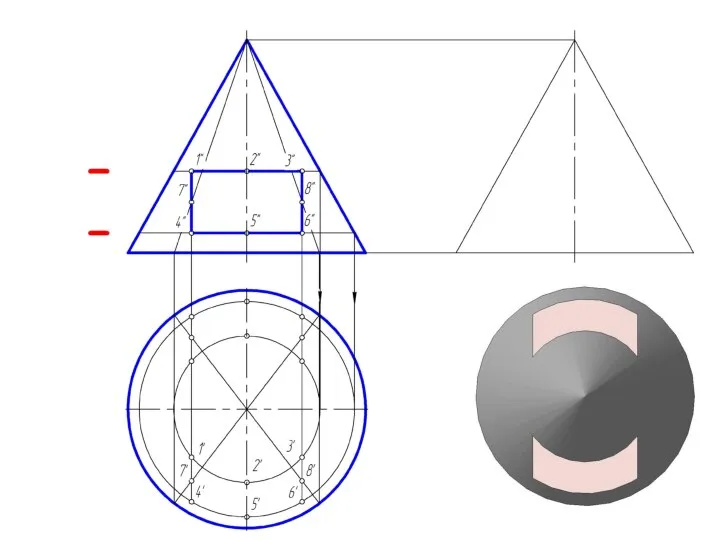
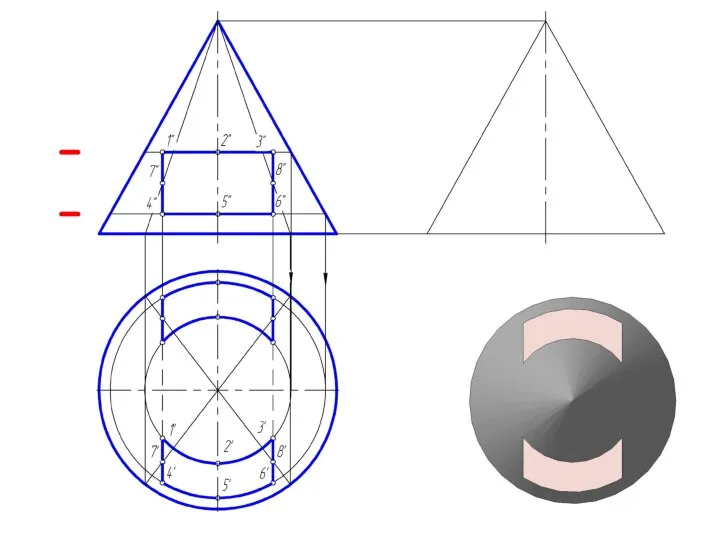
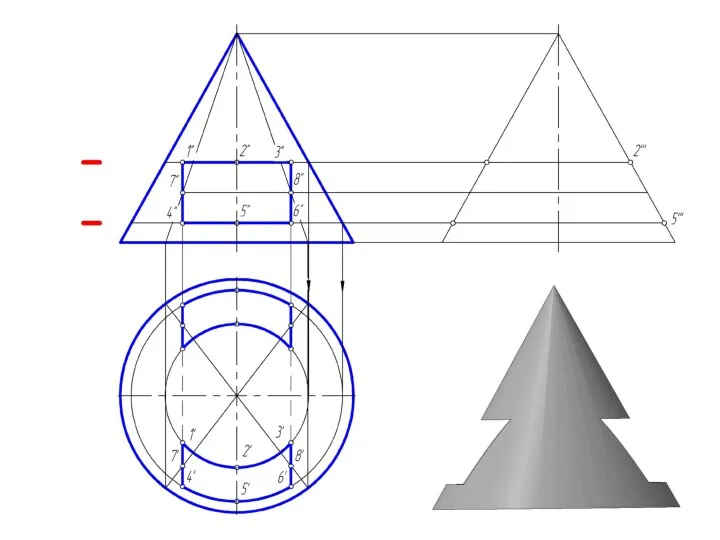
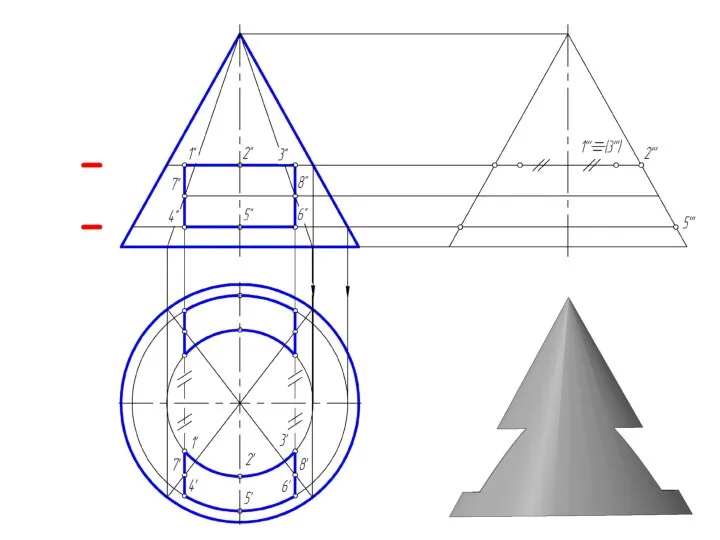
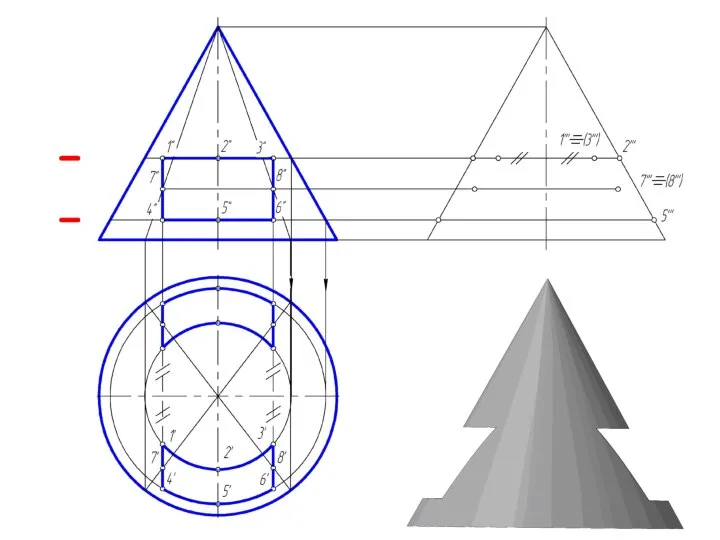
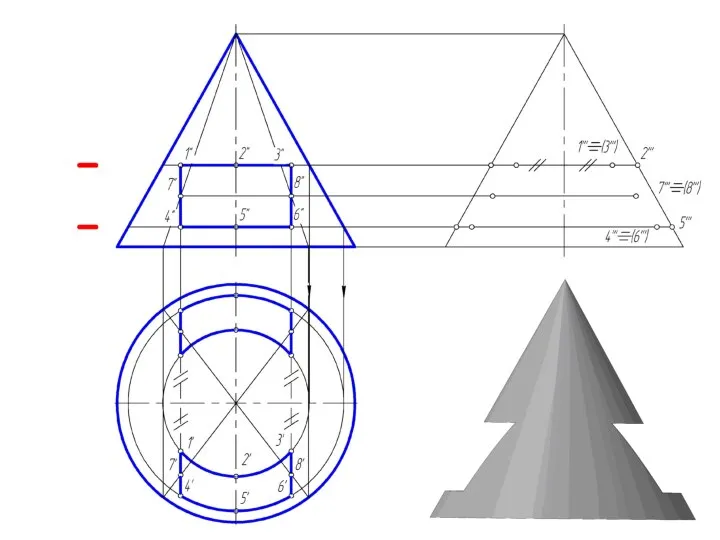
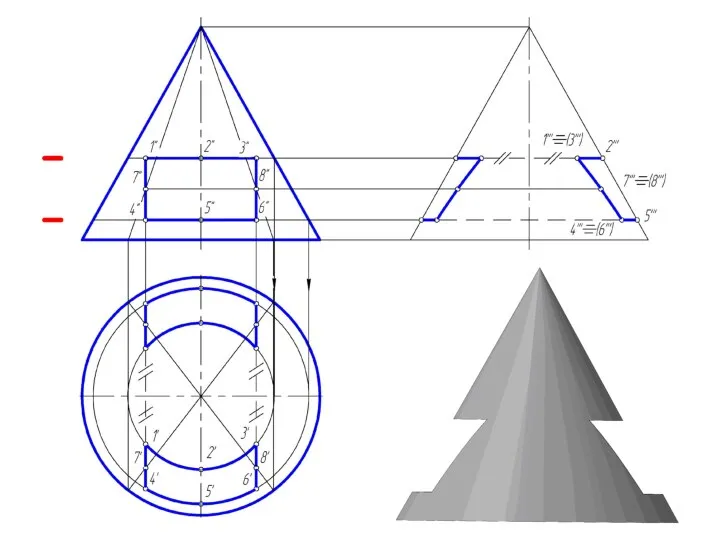
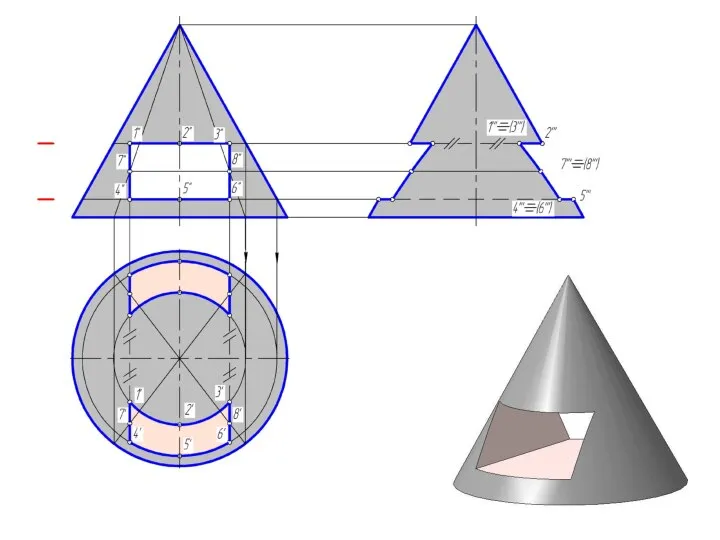
Пересечение прямого кругового конуса прямой линией
При определении точки пересечения прямой с поверхностью в качестве вспомогательной секущей плоскости выбирают проецирующую плоскость.
Использование вспомогательной проецирующей плоскости не всегда упрощает решение и в некоторых случаях целесообразно применять плоскости общего положения.
В случае задачи по определению точки пересечения прямой общего положения с поверхностью прямого кругового конуса необходимо ввести вспомогательную плоскость, проходящую через эту прямую и вершину конуса, чтобы получить в пересечении прямые линии.

Определить точки пересечения прямой m
с поверхностью прямого кругового конуса

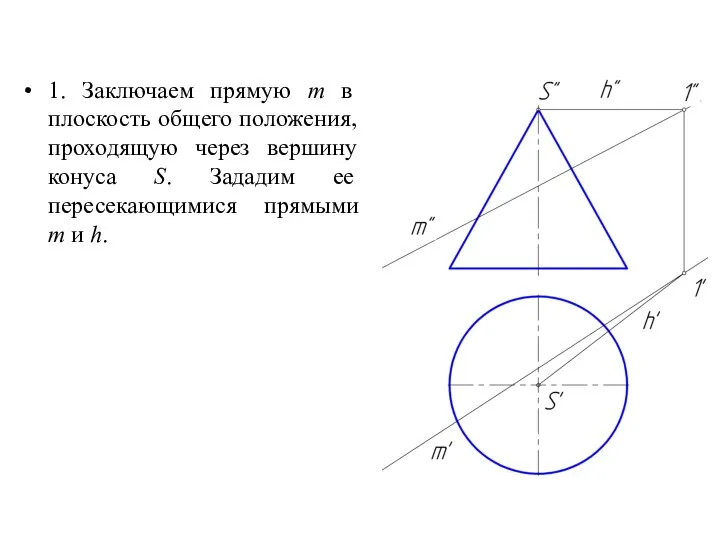
1. Заключаем прямую m в плоскость общего положения, проходящую через вершину конуса S. Зададим ее пересекающимися прямыми
m и h.

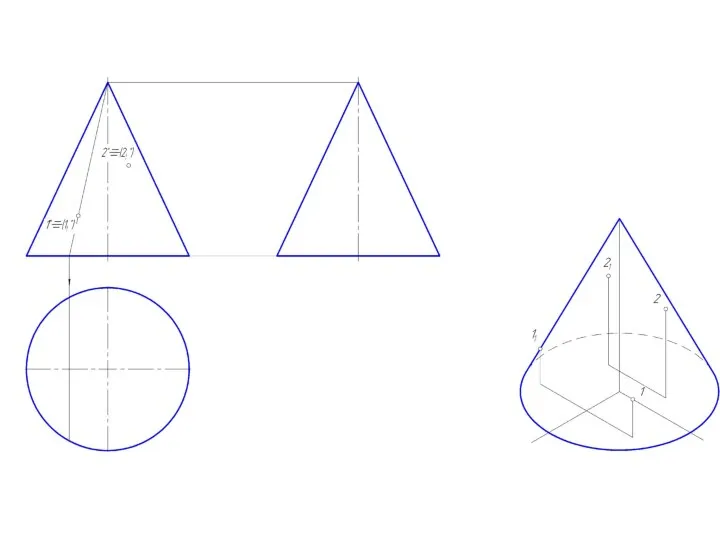
Определяем линию, по которой построенная плоскость пересекает плоскость H и основание конуса.
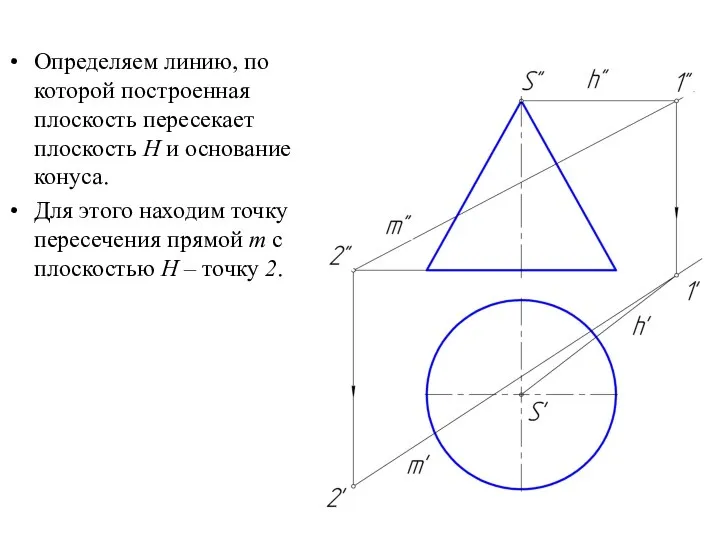
Для этого находим точку пересечения прямой m с плоскостью Н – точку 2.

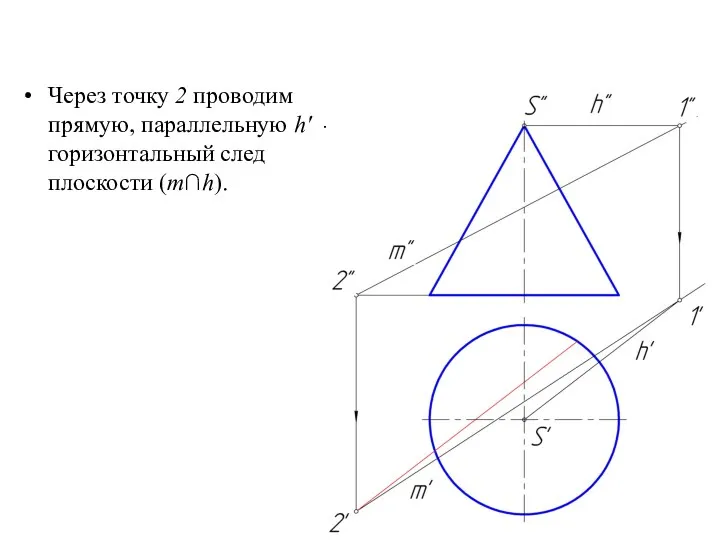
Через точку 2 проводим прямую, параллельную h' - горизонтальный след плоскости (m∩h).

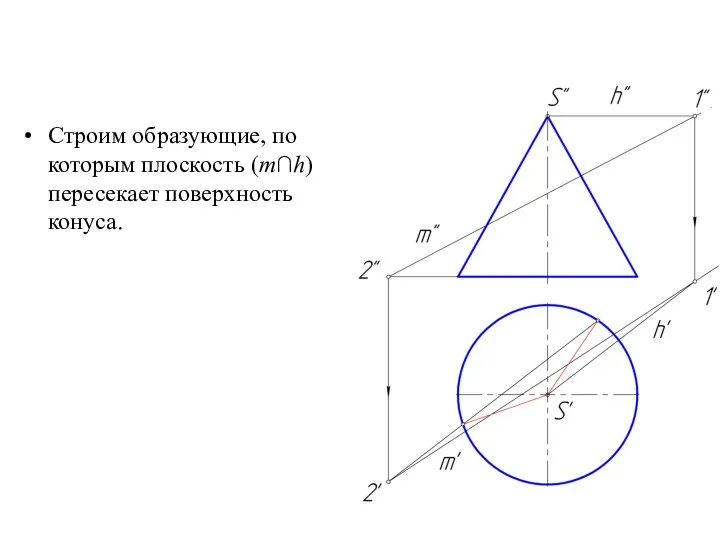
Строим образующие, по которым плоскость (m∩h) пересекает поверхность конуса.