Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами

Определение функции
Функция – это зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.
х – независимая переменная, аргумент функ-ции, абсцисса точки;
у – зависимая переменная, значение функции, ордината точки.

Если зависимость переменной у от переменной х является функцией, то коротко это записывают так:
у = f(х)
Пример.
у = 2х + 3 или f(х) = 2х + 3
Если х = 5, то f(5) = 2 5 + 3=10 + 3 = 13
Если f(х) = 0, то 2х + 3 = 0
2х = -3
х = -1,5

Область определения функции – все значения независимой переменной х.
Обозначение: D( f )
Область значений функции – все значения зависимой переменной у.
Обозначение: Е( f )
Если функция у = f(х) задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений х, при которых выражение f(х) имеет смысл.

y=f(x)

Пример. Найти область определения функции:
1) f(х) = 2х + 3
D(f)=R или D(f) = (- ; + )
2) f(х) = х +
2
3
x
D(f)=R или D(f) = (- ; + )
3) f(х) =
5x + 2
x - 8
D(f)= (- ; 8) (8; + )
х – 8 0
х 8
8

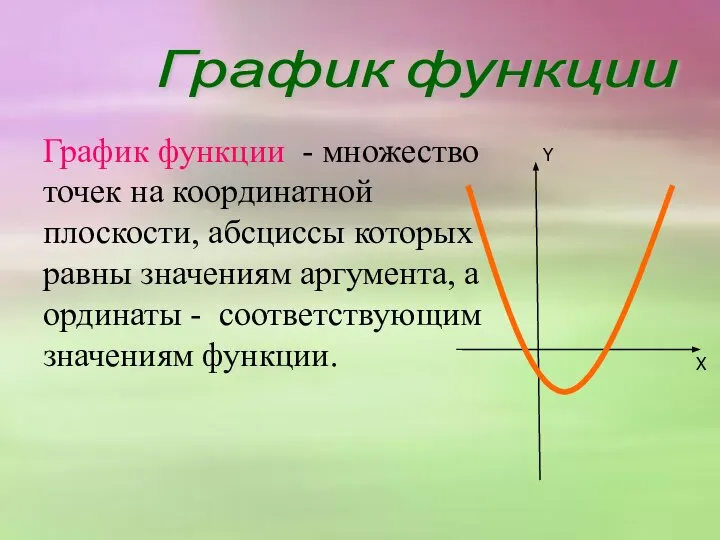
График функции - множество точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции.
График функции
X
Y

Табличный способ заключается в задании таблицы отдельных значений аргумента и соот-ветствующих им значений функции. Применя-ется в том случае, когда область определения функции является конечным множеством.
Способы задания функции

Аналитический способ заключается в установлении связи между аргументом и функцией с помощью формул.
Например, у = 2х + 1 у = 2х² у = ¼х + 8 и т.д.
Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.

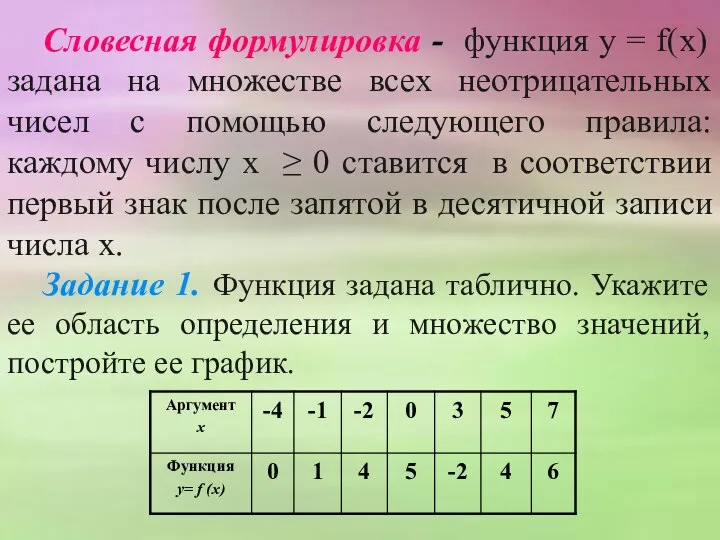
Словесная формулировка - функция у = f(х) задана на множестве всех неотрицательных чисел с помощью следующего правила: каждому числу х ≥ 0 ставится в соответствии первый знак после запятой в десятичной записи числа х.
Задание 1. Функция задана таблично. Укажите ее область определения и множество значений, постройте ее график.

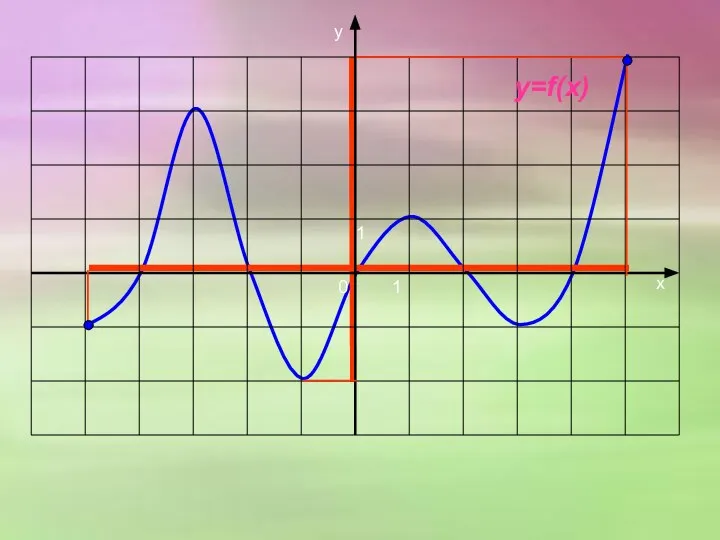
Задание 2. Функция задана аналитически
Задание 3. Функция задана графически. Найди-те область определения функции и область значений функции.
Выразите каждую переменную через две другие.

Существует несколько основ-ных видов функций:
линейная функция;
прямая пропорциональность;
обратная пропорциональность;
квадратичная функция;
кубическая функция;
функция корня;
функция модуля.
Виды функций

Линейная функция
функция вида y = k х + b
1. D( f ) = R;
E( f ) = R;
графиком функции является прямая
k>0
k<0
k=0

функция вида y = k х
1. D( f ) = R;
E( f ) = R;
графиком функции является прямая, проходящая через начало координат.
Прямая пропорциональность

Обратная пропорциональность
функция вида y = ;
1. D( f ) = (-∞;0) (0;∞)
2. E( f ) = (-∞;0) (0;∞);
3. графиком функции является гипербола
k
x
k>0
k<0

Квадратичная функция
функция вида y = x² ;
D( f ) = R;
2. E( f ) = [0;∞);
3. графиком функции является парабола

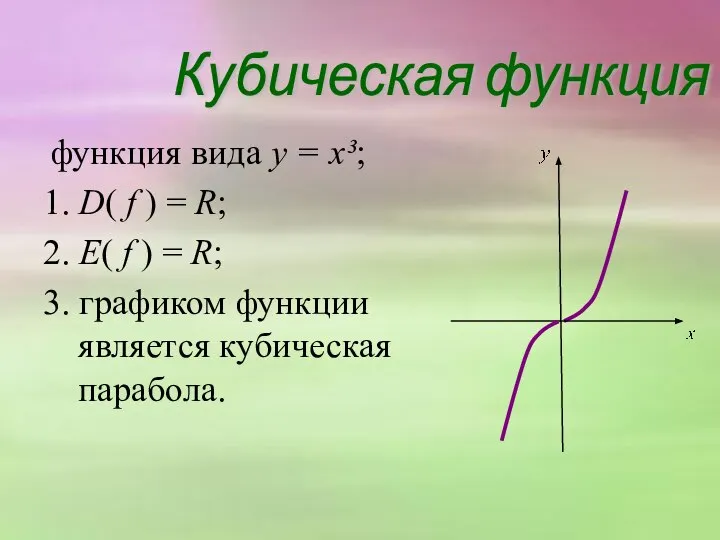
функция вида y = x³;
1. D( f ) = R;
2. E( f ) = R;
3. графиком функции является кубическая парабола.
Кубическая функция

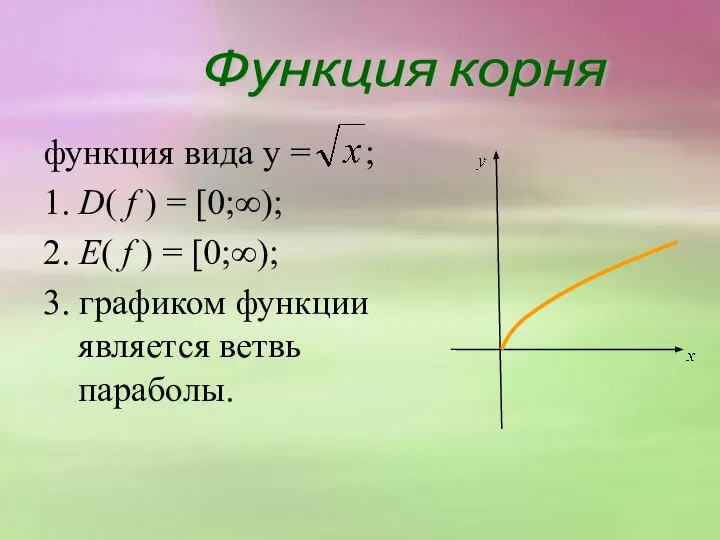
функция вида y = ;
1. D( f ) = [0;∞);
2. E( f ) = [0;∞);
3. графиком функции является ветвь параболы.
Функция корня

функция вида y = |x|;
1. D( f ) = R;
2. E( f ) = [0;∞);
3. график функции на промежутке [0;∞) совпадает с графиком функции у = х, а на промежутке (-∞;0] – с графиком функции у = -х
Функция модуля

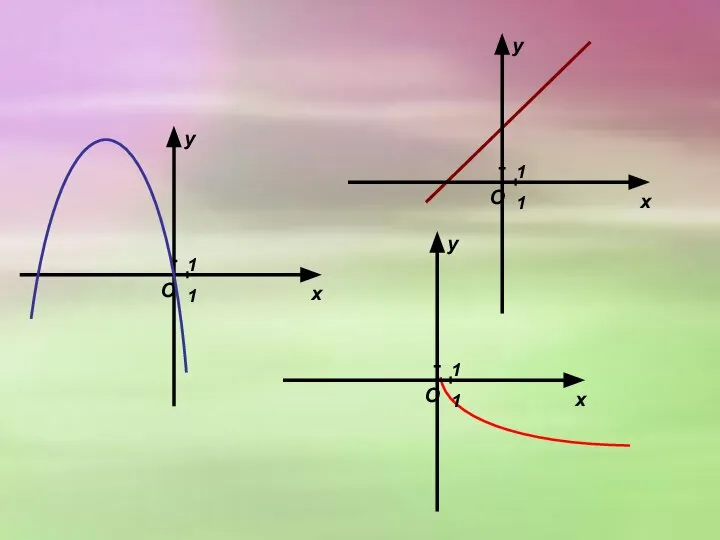
1. Каждый график соотнесите с соответствующей ему формулой:
y =
k
x
y = x²
y = 2x
y = 2x + 2