Линейная алгебра

Тема занятия
1.Значение математики.
2.Основные понятия линейной алгебры
-примеры систем, имеющих единственное решение, не имеющих решения и с бесконечным множеством решений;
-совместные, определенные и эквивалентные системы;
-матрица системы двух линейных уравнений;
определитель второго порядка;
3.Матрицы и определители
-определение и свойства матриц;
-главная и побочная диагональ определителя;
-системы двух линейных уравнений;
-миноры и алгебраические дополнения;
-вычисление определителя 3-го порядка.

ЛИНЕЙНАЯ АЛГЕБРА
Значение математики.
Процессы, описываемые с помощью математических формул могут иметь линейный или нелинейный вид. Линейный – когда все переменные входят в описание в первой степени. Нелинейные, когда переменные имеют степень отличную от единицы или связаны с какой-либо тригонометрической, логарифмической и иной функцией. Большинство процессов в первом приближении на определенном отрезке времени можно считать линейными, поэтому и появилось понятие ЛИНЕЙНАЯ АЛГЕБРА, которая описывает все, что связано с такими процессами.
Начнем изучение линейной алгебры от простого к сложному.
Рассмотрим три системы линейных уравнений с двумя неизвестными.
1.
X1=2; X2=3. Системы линейных уравнений со строго одним решением называются совместными и определенными.
2.
Умножив на 2 первое уравнение, получим: 2Х1+6Х2=2, (А)
Видим, что (А) и второе уравнение системы в левой части одинаковы, а в правой – различны, что говорит о невозможности иметь в системе одинаковые Х1 и Х2, то есть, такие системы линейных уравнений называются несовместными.

3.
В данной системе линейных уравнений второе получено умножением первого на 2. То есть, решение первой системы, например, Х1=4, Х2=9 (принято обозначать значения решения в виде (4;9)), или (6;14), или (40;19) и т.д. до бесконечности, подходит и для второй системы. Такие системы линейных уравнений называются совместными и неопределенными.
Конечно, стоит задача, как не решая уравнения, определить совместны они или нет. Для этого надо перейти к новому понятию МАТРИЦЫ и ОПРЕДЕЛИТЕЛИ. Выпишем коэффициенты уравнений как показано ниже:
2 -1 1 3 5 -1 Это матрицы или определители второго
1 1 2 6 10 -2 . порядка.
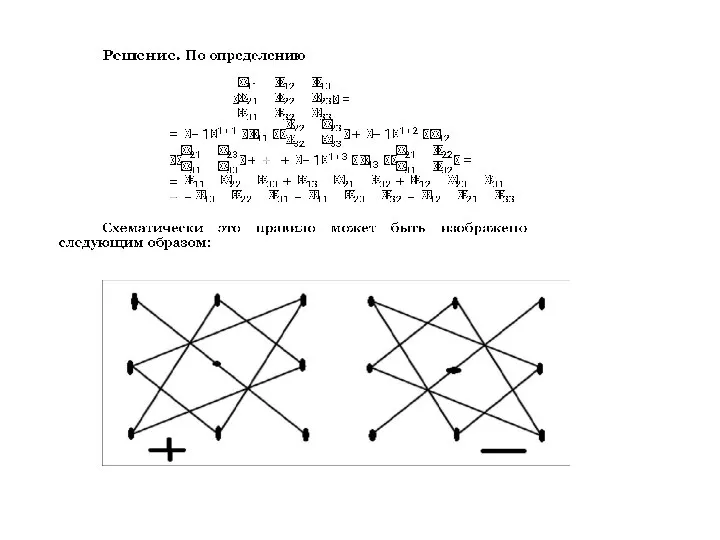
И посчитаем определитель матрицы (D) по схеме получим:
2*1 – (-1)*1 = 3 1*6 – 3*6 = 0 5*(-2) – (-1)*10 = 0.
Вывод: Если определитель матрицы коэффициентов не равен нулю, ту система линейных уравнений совместна, т.е. имеет решение. Если D равен нулю, то система несовместна или неопределенна.

Операция умножения двух матриц вводится только для случая, когда матрица А согласована с матрицей В. Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В. Отметим следующее:
Из согласованности матрицы А с матрицей В не следует согласованность матрицы В с матрицей А;
Если А и В – квадратные матрицы одного порядка, то они взаимно согласованы (А согласована с В, В согласована с А).

Указанные определения нужны для решения ЛУ

Матричные уравнения позволяют рассчитать неизвестную матрицу, связанную с исходной произведением.

ОПРЕДЕЛИТЕЛИ