Содержание
- 2. Информативность. Математические модели, сформированные на основе методов несущей и комплексной огибающей являются наиболее полными и универсальными.
- 3. Время моделирования. Максимальное время моделирования требуется для модели несущей, так как частота дискретизации должна в 5
- 4. Компьютерный эксперимент Компьютерный (вычислительный) эксперимент — метод изучения устройств или физических процессов с помощью моделирования. Он
- 5. Задачи, решаемые в ходе компьютерного эксперимента: • измерение показателей работоспособности РЭС, требования к которым сформулированы в
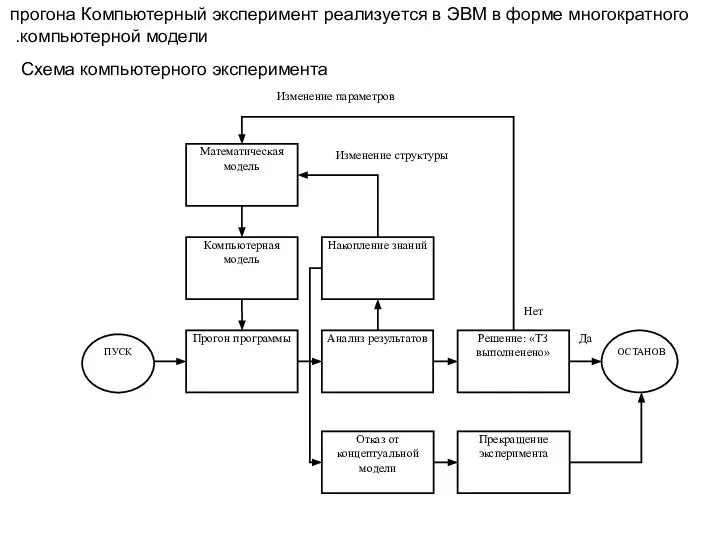
- 6. Схема компьютерного эксперимента Компьютерный эксперимент реализуется в ЭВМ в форме многократного прогона компьютерной модели.
- 7. Компьютерный эксперимент является автоматизированным процессом. Анализ результатов эксперимента, принятие решения и характер изменений в компьютерной модели
- 8. Если в процессе эксперимента не будет найдено решения, удовлетворяющего требованиям технического задания, то, очевидно, была принята
- 9. Планирование эксперимента Цель планирования эксперимента – получить максимум информации при минимуме опытов. X = (x1, x2,
- 10. Принципы, положенные в основу планирования эксперимента: 1. отказ от полного факторного анализа; 2. постепенное усложнение математической
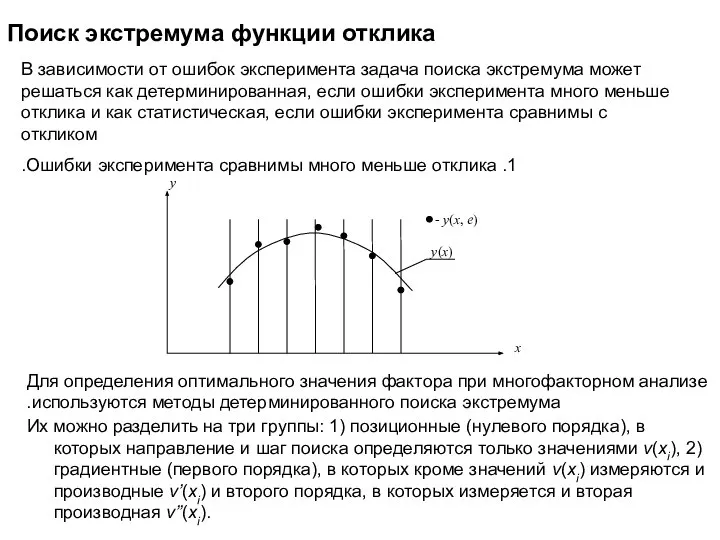
- 11. Поиск экстремума функции отклика В зависимости от ошибок эксперимента задача поиска экстремума может решаться как детерминированная,
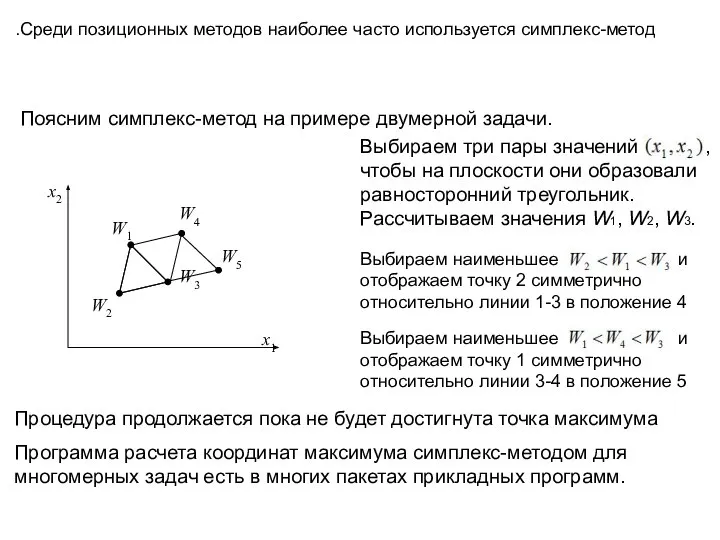
- 12. Поясним симплекс-метод на примере двумерной задачи. Процедура продолжается пока не будет достигнута точка максимума Программа расчета
- 14. Скачать презентацию








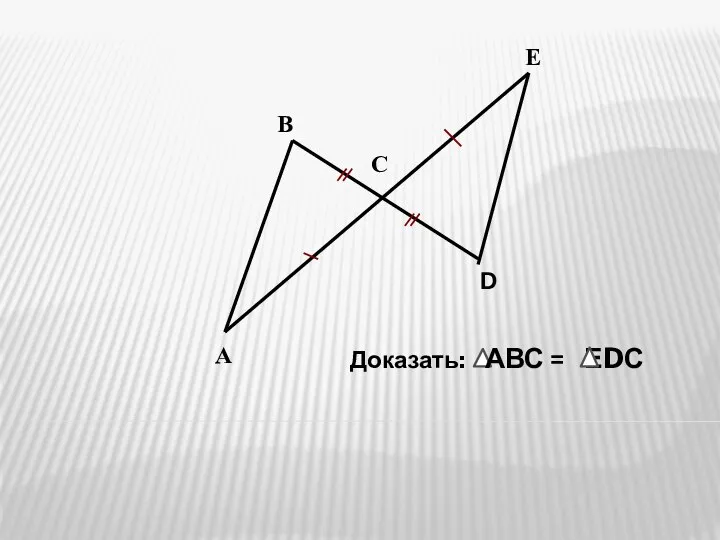 Признаки равенства треугольников. Решение задач
Признаки равенства треугольников. Решение задач Презентация на тему Случайные события и вероятность
Презентация на тему Случайные события и вероятность  Ломаная линия
Ломаная линия Презентация на тему КРАТНЫЕ И ДВОЙНЫЕ ИНТЕГРАЛЫ
Презентация на тему КРАТНЫЕ И ДВОЙНЫЕ ИНТЕГРАЛЫ  Схема Горнера. Формулы площадей
Схема Горнера. Формулы площадей Признаки подобия треугольников
Признаки подобия треугольников Алгебра логики. Понятие алгебры логики
Алгебра логики. Понятие алгебры логики Распределение случайных величин. Функция распределения и плотность распределения случайной величины
Распределение случайных величин. Функция распределения и плотность распределения случайной величины Письменный приём вычисления
Письменный приём вычисления Анализ задач и альтернативные методы решений. Мастер-класс
Анализ задач и альтернативные методы решений. Мастер-класс Графический метод решения уравнений с параметром
Графический метод решения уравнений с параметром ДЗ №25 стериометрия №5 (1)
ДЗ №25 стериометрия №5 (1) Разложение функций в степенные ряды
Разложение функций в степенные ряды Решение задач
Решение задач Спецификация КИМ ЕГЭ 2015 г. Проверяемые требования (умения)
Спецификация КИМ ЕГЭ 2015 г. Проверяемые требования (умения) Правильные многоугольники
Правильные многоугольники Умножение и деление степеней
Умножение и деление степеней Презентация на тему Угол между прямыми
Презентация на тему Угол между прямыми  Применение технологий Веб 2.0 на уроках математики
Применение технологий Веб 2.0 на уроках математики Математические загадки
Математические загадки Делениес остатком
Делениес остатком Прямоугольник. Свойства. Признаки. Формулы. Определение. Тест. Задачи
Прямоугольник. Свойства. Признаки. Формулы. Определение. Тест. Задачи Знакомство с линиями чертежа Ломаная
Знакомство с линиями чертежа Ломаная Монотонность функции
Монотонность функции Практическое применение треугольников в жизни
Практическое применение треугольников в жизни Графы. ЕГЭ задание 15. Урок 11 А
Графы. ЕГЭ задание 15. Урок 11 А Формулы сложения
Формулы сложения Введение понятия целого и дробного выражения
Введение понятия целого и дробного выражения