Содержание
- 2. ПОНЯТИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ Дифференциальное уравнение (ДУ) – это уравнение, в которое входит неизвестная функция под знаком
- 3. Если неизвестная функция является функцией одной переменной, то дифференциальное уравнение называют обыкновенным (сокращенно ОДУ – обыкновенное
- 4. ПОРЯДОК ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ Максимальный порядок производной неизвестной функции, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.
- 5. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ Решение дифференциального уравнения - это неявно заданная функция Ф(x, y) = 0 (в
- 7. Скачать презентацию




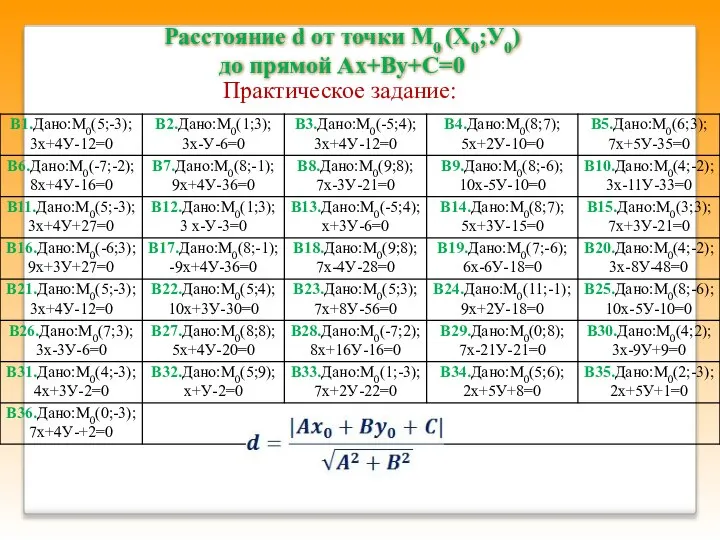 Перпендикуляр и наклонная
Перпендикуляр и наклонная Аналитическая панель
Аналитическая панель Пифагоровы тройки чисел
Пифагоровы тройки чисел Теорема Пифагора
Теорема Пифагора Задание 4. Числа, вычисления и алгебраические выражения
Задание 4. Числа, вычисления и алгебраические выражения Понятие вектора в пространстве
Понятие вектора в пространстве Применение комбинаторики и бинома Ньютона в теории вероятности
Применение комбинаторики и бинома Ньютона в теории вероятности Окружность. Основные теоремы
Окружность. Основные теоремы Всегда ли симметрично - это хорошо?
Всегда ли симметрично - это хорошо? Задачи на проценты
Задачи на проценты Граница круга
Граница круга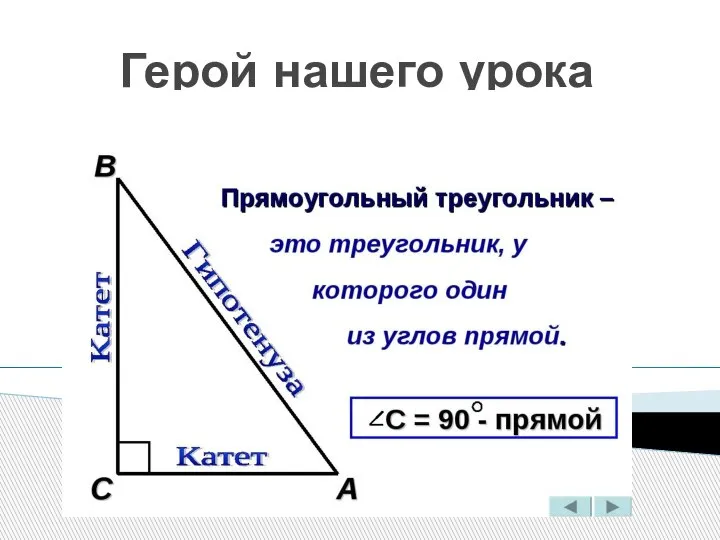 Площадь прямоугольного треугольника
Площадь прямоугольного треугольника pril
pril Движение. Центральная, осевая и зеркальная симметрии. Параллельный перенос
Движение. Центральная, осевая и зеркальная симметрии. Параллельный перенос Геометрическая прогрессия в экономике
Геометрическая прогрессия в экономике Веселая математика
Веселая математика Длина окружности и площадь круга. 6 класс
Длина окружности и площадь круга. 6 класс Изучение основ Анализа формальных понятий
Изучение основ Анализа формальных понятий Задача на тему: Прогрессия
Задача на тему: Прогрессия Золотое сечение. Витрувий
Золотое сечение. Витрувий Математическая разминка
Математическая разминка Движение в геометрии
Движение в геометрии Выделение целой части из неправильной дроби и представление смешанной дроби в виде неправильной
Выделение целой части из неправильной дроби и представление смешанной дроби в виде неправильной Правильные многогранникик
Правильные многогранникик Численные методы. Вычислительная математика
Численные методы. Вычислительная математика Числа от 1 до 9. Письмо цифры 9
Числа от 1 до 9. Письмо цифры 9 Доли и дроби. 5 класс Новоселова Е.А. МКОУ «Усть-Мосихинская СОШ»
Доли и дроби. 5 класс Новоселова Е.А. МКОУ «Усть-Мосихинская СОШ» Способы измерения объемов геометрических тел
Способы измерения объемов геометрических тел