Функции одной переменной (лекция № 1)

Математическим анализом называют систему дисциплин, которые объединены следующими характерными чертами.
Предметом их изучения являются количественные соотноше-ния действительного мира (в отличие от геометрических дисциплин, занимающихся пространственными его свойствами).
Эти соотношения выражаются с помощью числовых величин, но в отличие от арифметики и алгебры, где рассматриваются преимущест-венно постоянные величины (они характеризуют состояния), в анализе - это переменные величины, характеризующие процессы.
В основу изучения зависимости между переменными величинами кладутся понятия функции и предела.
Зачатки методов математического анализа были у древнегреческих математиков (Архимед, Евдокс Книдский).
Систематическое же развитие эти методы получили в XVII веке.
На рубеже XVII и XVIII веков И. Ньютон и Г.В. Лейбниц в общем и целом завершили создание дифференциального и интегрального исчисления, а также положили основу учения о рядах и дифферен-циальных уравнениях.
Леонард Эйлер в XVIII веке разработал два последних раздела и заложил основу других дисциплин математического анализа.
Дальнейшее развитие анализа связывают с именами таких ученых XIX и ХХ веков, как О.Л. Коши и М.Э.К Жордан во Франции,
Н.И. Лобачевский в России и
С.П. Новиков в СССР,
Н.Х. Абель в Норвегии,
Г.Ф.Б. Риман и
Г.Ф.Л.Ф. Кантор в Германии и др.

УЧЕБНЫЕ ВОПРОСЫ:
1. Понятие функции. Основные свойства
и классификация
2. Предел функции. Основные теоремы о пределах
3. Непрерывность функции

1. Красс М.С., Чупрынов Б.П. Математика для экономистов:
Учебное пособие. – СПб: Питер, 2016.
2. Ахтямов М.А. Математика для социологов и экономистов.
– М.: ФИЗМАТЛИТ, 2004.
3. Попов А.М. Сотников В. Н. Высшая математика для
экономистов: учебник и практикум для прикладного
бакалавриата. – М.: Изд. "Юрайт", 2014.
4. Высшая математика для экономического бакалавриата:
Учебник и практикум / Под ред. проф. Кремера Н.Ш. – М.: Изд. "Юрайт", 2016.
Литература

Понятие функции. Основные свойства и классификация
ПЕРВЫЙ ВОПРОС

Определение.
Правило f, сопоставляющее каждому числу х ∈ X ⊆ R единст-венное число у ∈ Y ⊆ R, называется функцией у = f (х), заданной на множестве X и принимающей значения в множестве Y.
Ахтямов А. М. «Математика для социологов и экономистов».
Определение.
Множество X называется областью определения (задания) функции у = f (х), а множество Y – областью значений (изме-нения) функции .
При этом переменная х называется аргументом функции или независимой переменной, а элемент у, соответствующий конкретному элементу х – значением функции у = f (х) в точке х.
Замечание.
Если множество X специально не оговорено, то под областью определения функции подразумевается область допустимых зна-чений независимой переменной х.

Определение.
Функция называется явной, если она задается формулой у = f (х),
в которой правая часть не содержит зависимой переменной, например, y = 2 x + 1.
Определение.
Функция у аргумента х называется неявной, если она задана уравнением F(x, y) = 0, не разрешенным относительно зависимой переменной, например, y – 2 x - 1 = 0, y + sin y – 2 x + 7 = 0.
Определение.
Параметрическим представлением функции называется разновидность представления переменных, когда их зависимость выражается через дополнительную величину – параметр.
Предположим, что функциональная зависимость y от x задана через промежуточную величину – t.
Тогда формулы x = φ (t) и y = ψ (t) задают параметрическое представление функции одной переменной.

Определение.
Пусть у = f (х) есть функция независимой переменной х, опре-деленной на множестве Х с областью значений Y. При этом каж-дому y ∈ Y соответствует единственное значение х ∈ Х такое, что f (х) = у.
Тогда полученная функция x = φ (у),
определенная на множестве Y с областью
значений Х, называется обратной.
Обозначение: у = f -1(х).
Графики взаимно обратных функций сим-
метричны относительно биссектрисы первого
и третьего координатных углов
Определение.
Если функция у = f (u) есть функция переменной u (определен-ной на множестве U с областью значений Y ), а переменная u, в свою очередь, также является функцией u = φ (х) (определенной на множестве X с областью значений U ), то заданная на мно-жестве X функция у = f (φ (х)) называется сложной функцией.

Определение.
Уравнение F(x, y) = 0 называется уравнением линии L на плоскости (в заданной системе координат), если этому урав-нению удовлетворяют координаты x и y любой точки, лежащей на линии L, и не удовлетворяют координаты никакой точки, не лежа-щей на этой линии.
Определение.
Графиком функции y = f (x) (F(x, y) = 0) называется множество точек (x, y) плоскости, координаты которых удовлетворяют этой формуле (уравнению).

ПРЕОБРАЗОВАНИЯ ГРАФИКОВ:
1. у = f (х + а) – сдвигает график у = f (х) параллельно оси Ох на |а| единиц (а > 0 – влево, а < 0 – вправо).
2. у = f (х) + b – сдвигает график у = f (х) параллельно оси Оу на |b| единиц (b > 0 – вверх, b < 0 – вниз).
3. у = m f (х) (m ≠ 0) – растягивает (m > 1) или сжимает (0 < m < 1) в m раз график у = f (х) относительно оси Оу.
При m < 0, кроме того, симметрично отображает график относительно оси Ох.
4. у = f (kх) (k ≠ 0) – сжимает (k > 1) или растягивает (0 < k < 1) в k раз график у = f (х) относительно оси Ох.
При k < 0, кроме того, симметрично отображает график относительно оси Оу.

Основные элементарные функции:
а) степенная функция у = х n;
б) показательная функция у = а x, а > 0, а ≠ 1
(X = (-∞; +∞); Y = (0; +∞));
в) логарифмическая функция y = loga x, а > 0, а ≠ 1
(X = (0; +∞); Y = (-∞; +∞));
г) тригонометрические функции
y = sin x, y = cos x,
y = tg x, y = ctg x;
д) обратные тригонометрические функции
у = arcsin х, у = arccos х,
у = arctg x, у = arcctg х.
Определение.
Элементарными называются функции, построенные из основных элементарных функций при помощи конечного числа алгебраических действий и конечного числа операций образо-вания сложной функции.

Предел функции. Основные теоремы о пределах
ВТОРОЙ ВОПРОС

Определение.
Если каждому числу из натурального ряда чисел 1, 2, ..., n, ... поставлено в соответствие вещественное число xn, то множество вещественных чисел x1, x2, ..., xn, ... называется числовой после-довательностью.
Числа x1, x2, ..., xn, ... называются элементами или членами последовательности, xn – общим членом последователь-ности, а число n – его номером.
Обозначение последовательности { x1, x2, ..., xn, ... }: { xn }.
Определение*.
Последовательностью элементов числового множества R называется отображение f, определенное на множестве нату-ральных чисел N и принимающее значения в множестве R , т.е.
f : N → R.
Элементом или членом последовательности f называет-ся упорядоченная пара (п, х), х = f (п), п ∈ N, х∈ R.
Натуральное число п называется номером элемента после-довательности, а число х∈ R – его значением.
Примеры.
а) xn = const;
б) xn = n т.е. { xn } равна { 1, 2, 3, ... } – натуральные числа;
в) xn = 1/n т.е. { xn } равна { 1, 1/2, 1/3, ... };
г) xn = n·(-1)n т.е. { xn } равна { -1, 2, -3, 4, ... }.

Определение.
Правило f, сопоставляющее каждому числу х ∈ X ⊆ R единст-венное число у ∈ Y ⊆ R, называется функцией у = f (х), заданной на множестве X и принимающей значения в множестве Y.

Теорема.
Определения предела функции по Гейне и по Коши экви-валентны.

Определение.
Число A называется левым (правым) пределом функции f (х) в точке х0, если для любого наперед взятого числа ε > 0 найдется отвечающее ему число δ = δ(ε) > 0 такое, что для всех х ≠ х0 и удов-летворяющих условию х0 - δ < х < х0 ( х0 < х < х0 + δ ), выполняется неравенство | f (x) – A | < ε:
Пример.
Функция f (х) = sgn х имеет в точке х0 = 0 правый и левый пределы.
Теорема.
Функция f (х) имеет в точке х0 предел тогда и только тогда, когда в этой точке существуют как правый, так и левый пределы, и они равны.

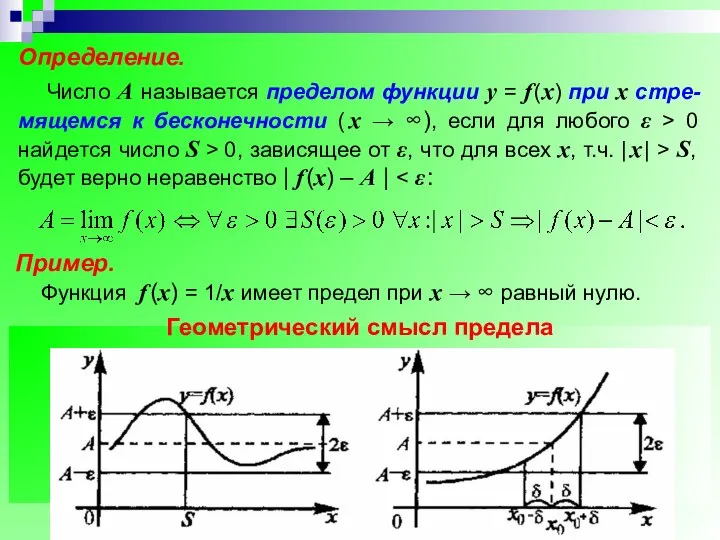
Определение.
Число А называется пределом функции у = f (х) при х → +∞ ( х → -∞), если для любого ε > 0 найдется число S > 0, зависящее от ε, что для всех х > S ( х < - S ), будет верно неравенство
| f (x) – A | < ε.
Пример.
Функция f (x) = 1/x имеет предел при x → ∞ равный нулю.

Теорема.
Если функция α(х) – бесконечно малая величина при х → х0 (х → ∞), то функция f (х) = 1/α(х) является бесконечно большой, и обратно, если f (х) – бесконечно большая функция при х → х0 (х → ∞), то α(х) = 1/ f (х) является бесконечно малой величиной.
Замечание.
Бесконечно большая величина есть функция неограниченная при х → х0 (х → ∞), однако неограниченная функция не обяза-тельно является бесконечно большой величиной.
Пример.
Функция y = x∙sin x является неограниченной, но не бесконеч-но большой.

Непрерывность функции
ТРЕТИЙ ВОПРОС

Определение.
Функция f (x) называется непрерывной в точке x0, если она удовлетворяет следующим условиям:
1) определена в точке x0 (существует f (x0));
2) имеет конечный предел при х → х0;
3) этот предел равен значению функции в точке х0:
Пример.
Исследовать непрерывность в точке х0 = 0 заданных функций.

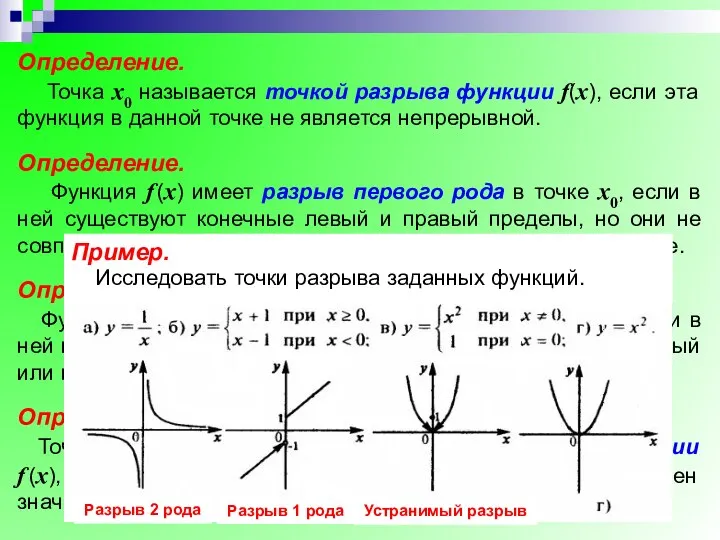
Определение.
Точка х0 называется точкой разрыва функции f(x), если эта функция в данной точке не является непрерывной.
Определение.
Функция f (x) имеет разрыв первого рода в точке х0, если в ней существуют конечные левый и правый пределы, но они не совпадают между собой или со значением функции в этой точке.
Определение.
Функция f (x) имеет разрыв второго рода в точке х0, если в ней не существует хотя бы один конечный односторонний (левый или правый) предел.
Определение.
Точка х0 называется точкой устранимого разрыва функции f (x), если предел функции при х → х0 существует, но не равен значению функции в этой точке.
Разрыв 2 рода
Разрыв 1 рода
Устранимый разрыв

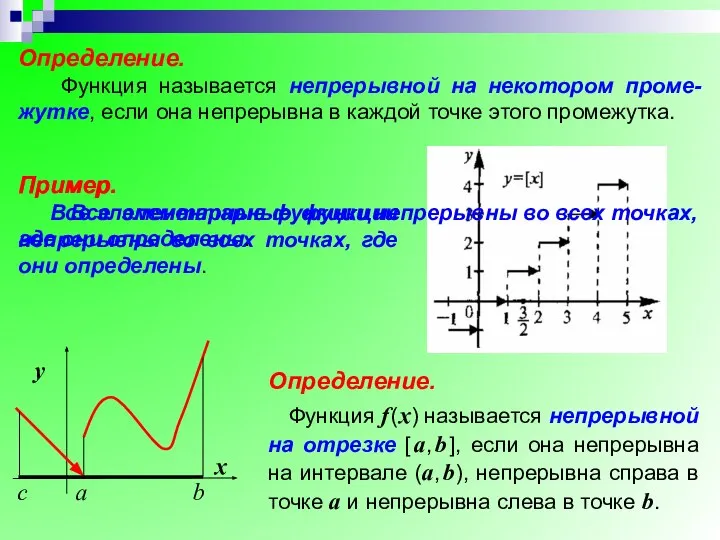
Пример.
Все элементарные функции непрерывны во всех точках, где они определены.
с
Пример.
Все элементарные функции непрерывны во всех точках, где они определены.