Функция у=ах²+вх+с

Повторим свойства функции у=ах² при а>0,а<0.
1)Определите направление ветвей параболы: а) у=3х²; б)у=-1/3х².
2)Выделите полный квадрат из квадратного трехчлена: а)х²-6х+7 ; б)у=х²-2х+3.

а)х²-6х+7=х²-2*3х+9-2=(х-3)²-2;
б)х²-2х+3=х²-2х+1+2=(х-1)²+2.
Проверим решение:

Построим в одной координатной плоскости графики функций:у=х²,у=(х-1)² и у=х²-2х+3,
1)у=(х-1)²
2)у=х²-2х+3= =(х-1)²+2

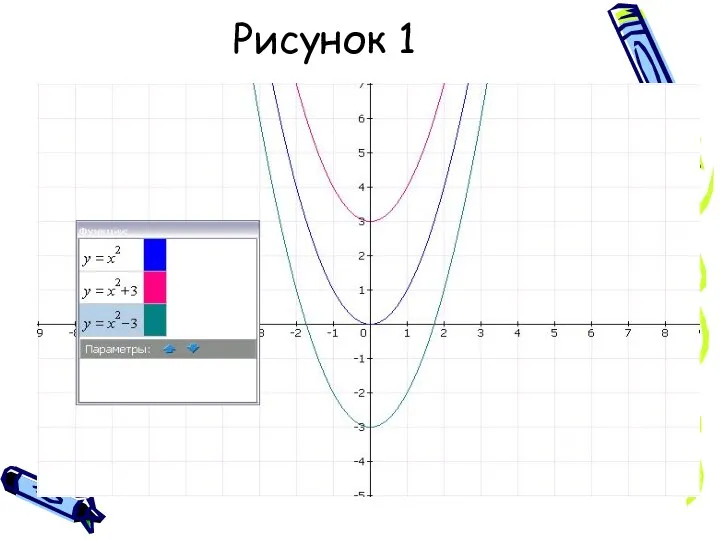
Графики функций:
Х=1 –ОСЬ СИММЕТРИИ ДЛЯ У=(Х-1)²+2
С помощью шаблона сравните параболы у=х² и у=(х-1)².
Сделайте вывод.
Теперь сравните графики функций у=(х-1)² и у=(х-1)²+2

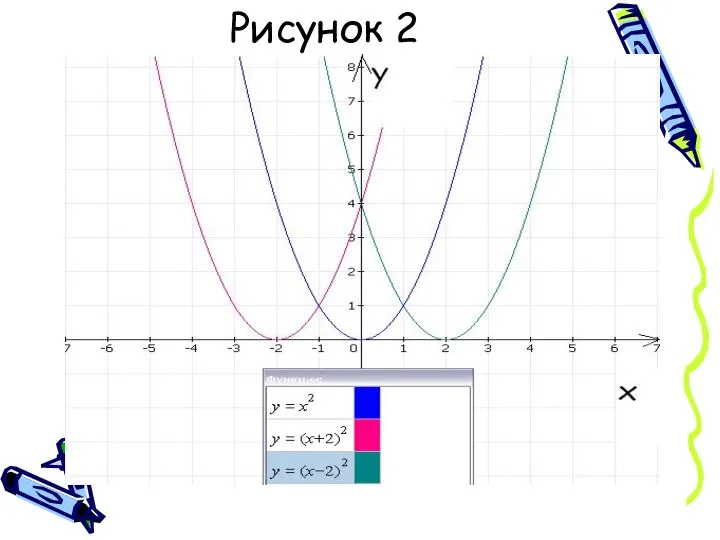
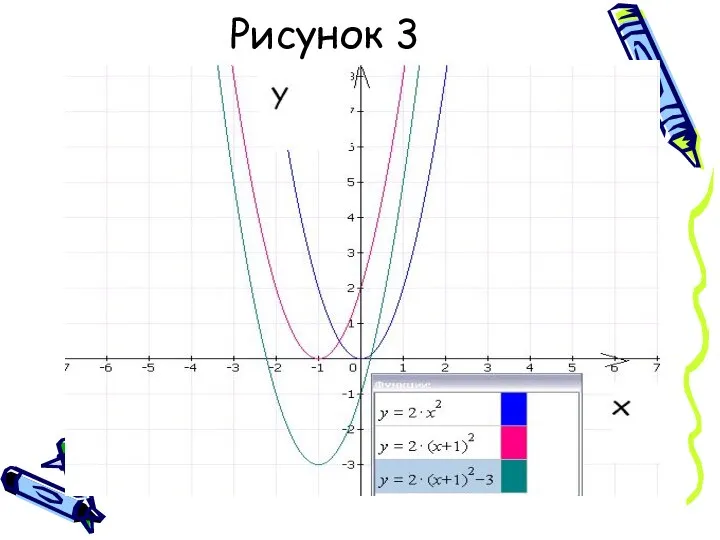
Сделаем вывод:
Графиком функции у=а(х-х0)²+у0 является парабола,получаемая сдвигом параболы у=ах² - вдоль оси абсцисс вправо на х0, если х0>0 ; влево на /х0/, если х0<0; -вдоль оси ординат вверх на у0 , если у0>0; вниз на /у0/,если у0<0.
Координаты вершины параболы равны (х0;у0).

Рассмотрим пример.
Найти координаты вершины параболы:
1) у=2(х-4)²-3; 2) у= -(х+2)²+1.
Решение:
1) Сравним с формулой у=а(х-х0)²+у0.
Так как (х0;у0)-вершина параболы,то х0=4, у0=-3.Координаты вершины (4;-3).
2)х0=-2; у0=1.

Рисунок 1

Рисунок 2

Рисунок 3