Содержание
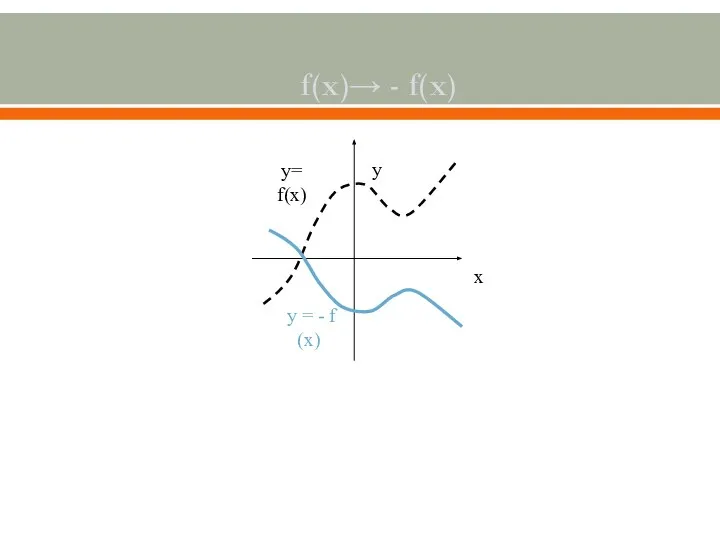
- 2. f(x)→ - f(x) у= f(х) у = - f (х) у х
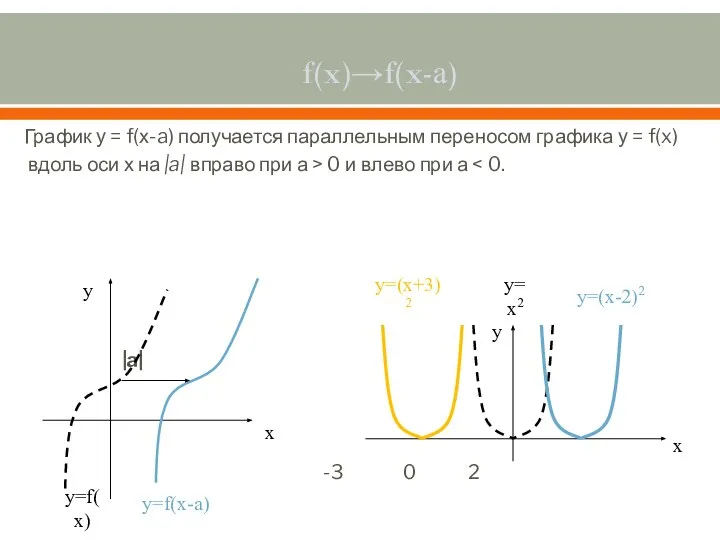
- 3. f(x)→f(x-а) График у = f(х-a) получается параллельным переносом графика у = f(x) вдоль оси х на
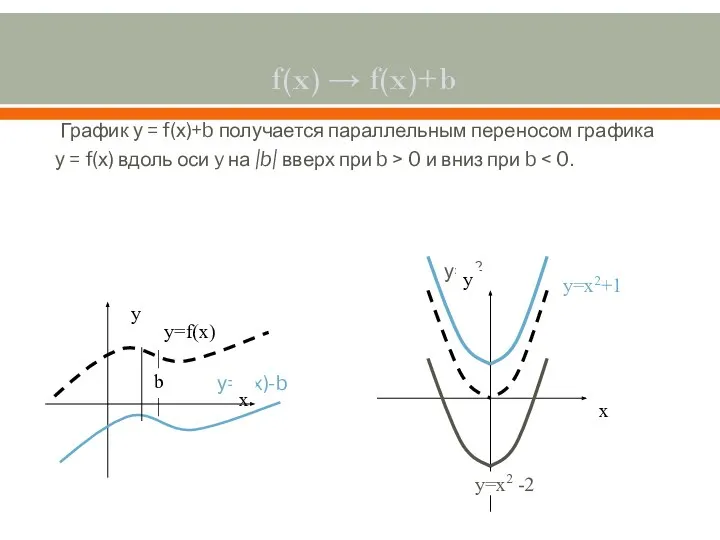
- 4. f(x) → f(x)+b График у = f(х)+b получается параллельным переносом графика у = f(х) вдоль оси
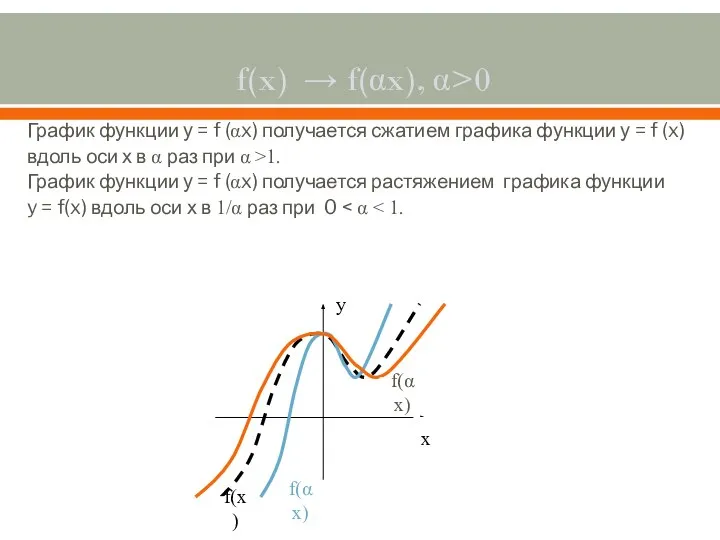
- 5. f(x) → f(αx), α>0 График функции у = f (αx) получается сжатием графика функции у =
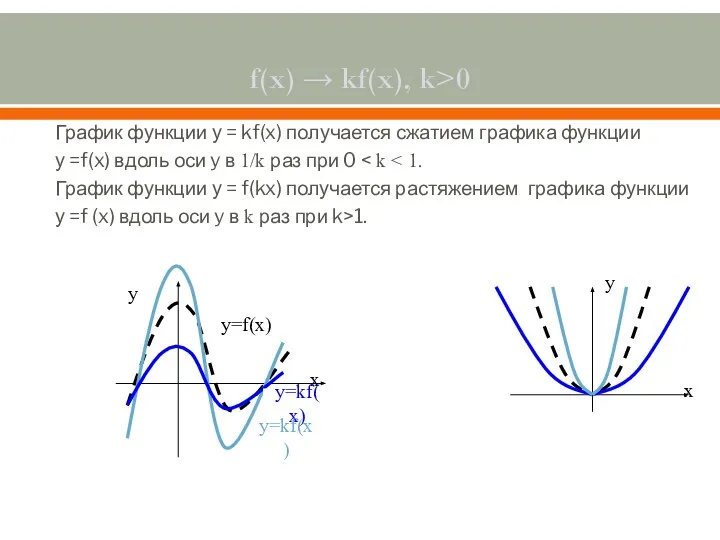
- 6. f(x) → kf(x), k>0 График функции у = kf(x) получается сжатием графика функции у =f(x) вдоль
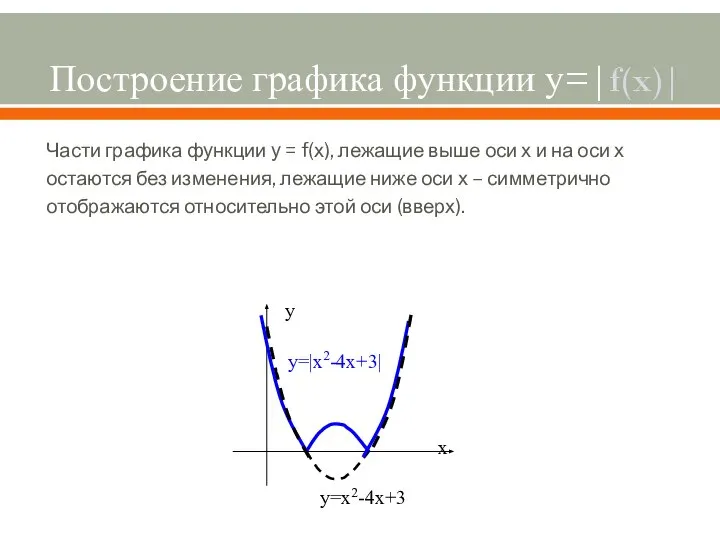
- 7. Построение графика функции у=|f(x)| Части графика функции у = f(х), лежащие выше оси х и на
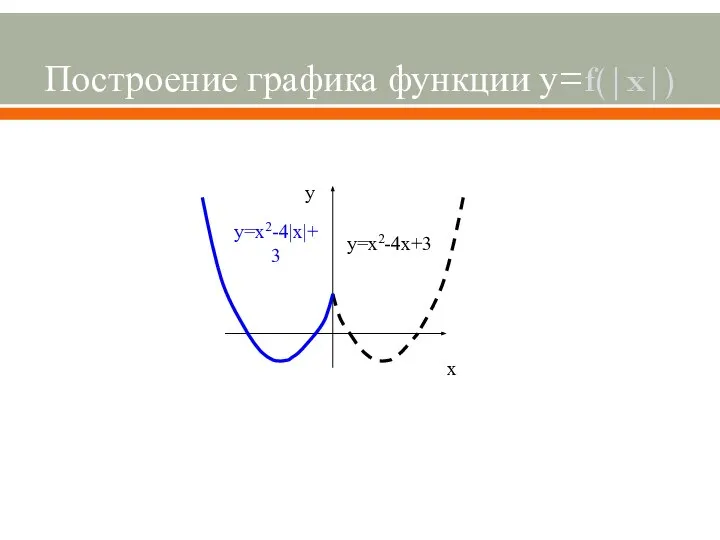
- 8. Построение графика функции у=f(|x|) у y=x2-4|x|+3 х y=x2-4x+3
- 10. Скачать презентацию
 Формулы сложения. Тригонометрические формулы
Формулы сложения. Тригонометрические формулы 3_TEMA_3_Matematicheskaya_logika_1
3_TEMA_3_Matematicheskaya_logika_1 Бинарные отношения
Бинарные отношения Презентация на тему Простые и составные числа
Презентация на тему Простые и составные числа  Поиски математики. Игра
Поиски математики. Игра Презентация на тему ОТРЕЗОК. ДЛИНА ОТРЕЗКА
Презентация на тему ОТРЕЗОК. ДЛИНА ОТРЕЗКА  Выборочное наблюдение
Выборочное наблюдение Презентация на тему Задачи на построение (7 класс)
Презентация на тему Задачи на построение (7 класс)  Элементы теории вероятностей
Элементы теории вероятностей Функции одной переменной (лекция № 1)
Функции одной переменной (лекция № 1) Линейная регрессия
Линейная регрессия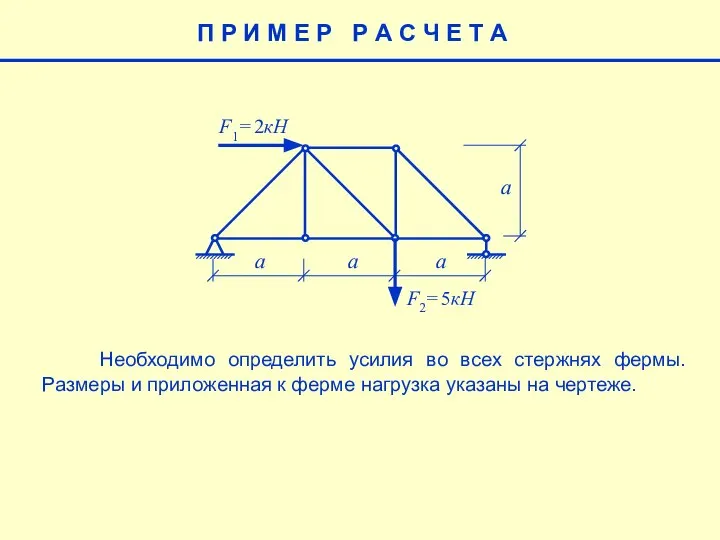 Методы расчета ферм
Методы расчета ферм Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике)
Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике) Выборочное наблюдение. Статистическое наблюдение
Выборочное наблюдение. Статистическое наблюдение Трапеция. Свойство углов равнобедренной трапеции
Трапеция. Свойство углов равнобедренной трапеции Изучаем геометрические фигуры. Дидактическая игра: На что похоже?
Изучаем геометрические фигуры. Дидактическая игра: На что похоже? 2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию
2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию Презентация на тему КВН по информатике и математике
Презентация на тему КВН по информатике и математике  Презентация на тему Многогранники
Презентация на тему Многогранники  Свойства степеней с натуральными показателями
Свойства степеней с натуральными показателями Числа 1 – 10. Сложение и вычитание
Числа 1 – 10. Сложение и вычитание Высота, биссектриса и медиана треугольника
Высота, биссектриса и медиана треугольника Методы оценки рисков проекта
Методы оценки рисков проекта Преобразования графика квадратичной функции. Преобразования графика
Преобразования графика квадратичной функции. Преобразования графика Преобразование графиков
Преобразование графиков Множества и операции над ними (9 класс)
Множества и операции над ними (9 класс) Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Геметрические построения. Анимированные алгоритмя
Геметрические построения. Анимированные алгоритмя