Содержание
- 2. Понятие функции Если каждому значению х из некоторого множества чисел поставлено в соответствие число у, то
- 3. Область определения и множество значений функции Областью определения функции называют множество всех значений, которые может принимать
- 4. Решение: Поскольку – многочлен, то область определения – все действительные значения х: Решение: Учитывая, что знаменатель
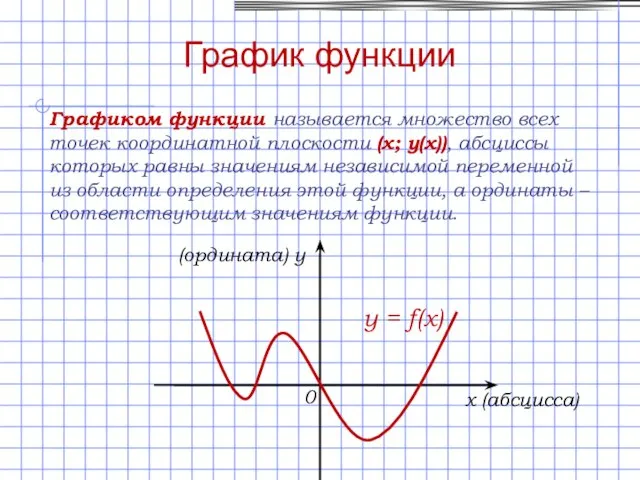
- 5. График функции Графиком функции называется множество всех точек координатной плоскости (х; у(х)), абсциссы которых равны значениям
- 6. аналитический (с помощью формулы); графический (с помощью графика); табличный (с помощью таблицы значений); словесный (правило задания
- 7. Вспомним основные элементарные функции и их графики
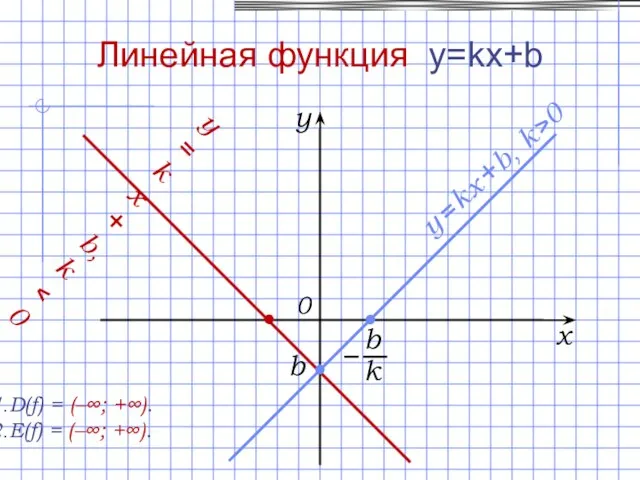
- 8. Линейная функция y=kx+b D(f) = (–∞; +∞). E(f) = (–∞; +∞). x y 0 b y
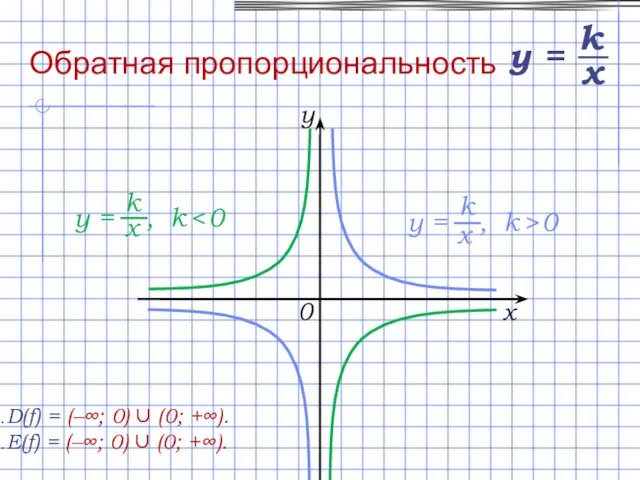
- 9. D(f) = (–∞; 0) ∪ (0; +∞). E(f) = (–∞; 0) ∪ (0; +∞). Обратная пропорциональность
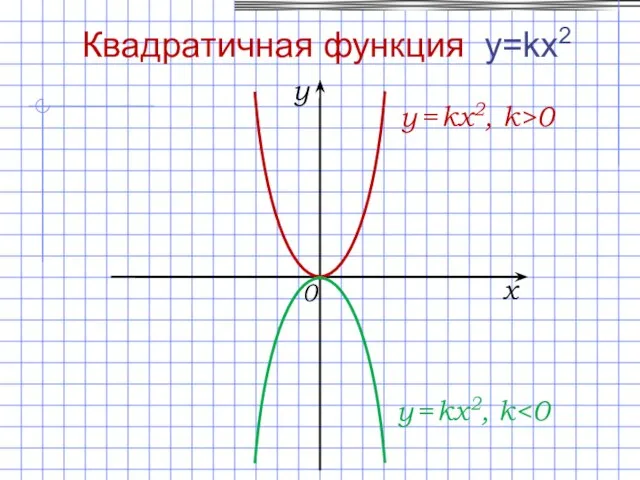
- 10. Свойства функции y = kx2 при k > 0: D(f) = (–∞; +∞). E(f) = [0;
- 11. 0 x y y = kx2, k>0 Квадратичная функция y=kx2 y = kx2, k
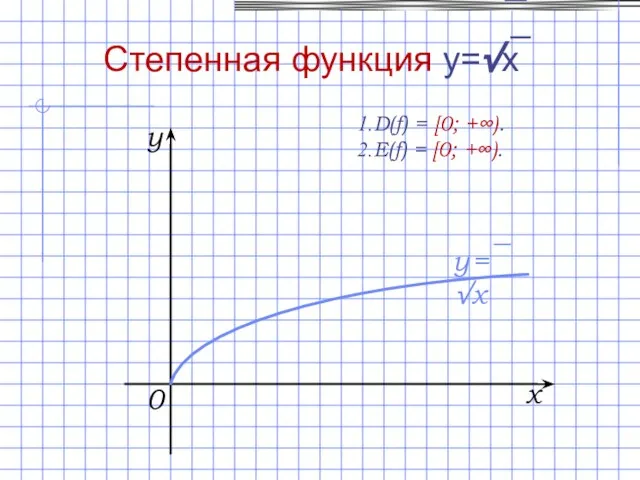
- 12. D(f) = [0; +∞). E(f) = [0; +∞). 0 x y
- 14. Скачать презентацию






 Геометрические портреты
Геометрические портреты Логарифм
Логарифм Множества. Операции над ними
Множества. Операции над ними Компьютерное моделирование процесса подготовки РКН к пуску. Лекция 15
Компьютерное моделирование процесса подготовки РКН к пуску. Лекция 15 Квадратичная функция
Квадратичная функция Презентация на тему Решаем задачи (1 класс)
Презентация на тему Решаем задачи (1 класс)  Интегривование тригонометрических функций
Интегривование тригонометрических функций Аппроксимация функций. Метод Лагранжа
Аппроксимация функций. Метод Лагранжа Презентация на тему Теория вероятностей и комбинаторные правила
Презентация на тему Теория вероятностей и комбинаторные правила  О математическом языке
О математическом языке Формулы сокращенного умножения. Интерактивный плакат
Формулы сокращенного умножения. Интерактивный плакат Графический диктант. Тема: Делимость чисел
Графический диктант. Тема: Делимость чисел Устный счёт
Устный счёт Площади и объемы
Площади и объемы Преобразование логарифмических выражений
Преобразование логарифмических выражений Решение задач по теме Арифметическая прогрессия
Решение задач по теме Арифметическая прогрессия Моделирование при управлении рисками авиапредприятий
Моделирование при управлении рисками авиапредприятий Методика изучения массы
Методика изучения массы Единицы измерения длины. Задания
Единицы измерения длины. Задания Показатели надежности электроснабжения
Показатели надежности электроснабжения Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений Больше, меньше, столько же
Больше, меньше, столько же Свойство противоположных сторон прямоугольника
Свойство противоположных сторон прямоугольника Санкт-Петербург на уроках математики
Санкт-Петербург на уроках математики formuly_privedenia
formuly_privedenia Решение уравнений. Буквенные выражения
Решение уравнений. Буквенные выражения Неопределённый интеграл
Неопределённый интеграл Формулы дифференцирования
Формулы дифференцирования