Содержание
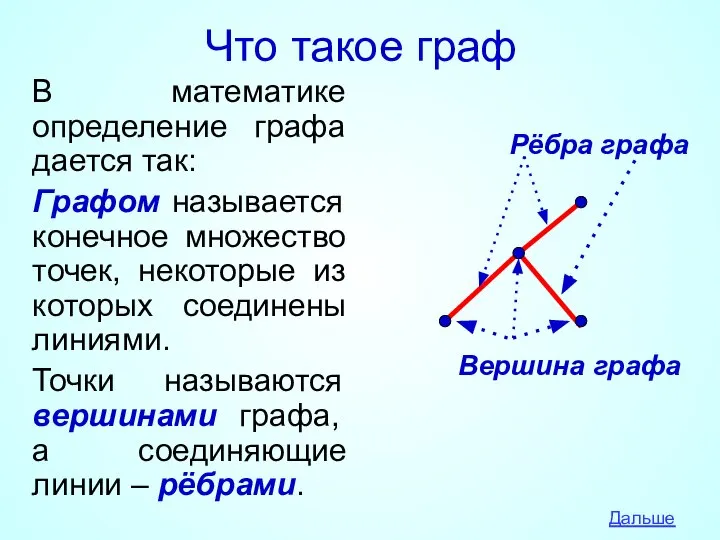
- 2. Что такое граф В математике определение графа дается так: Графом называется конечное множество точек, некоторые из
- 3. История возникновения графов Основы теории графов как математической науки заложил в 1736 г. Леонард Эйлер, рассматривая
- 4. Задача о Кенигсбергских мостах Бывший Кенигсберг (ныне Калининград) расположен на реке Прегель. В пределах города река
- 5. Задача о Кенигсбергских мостах Кенигсбергцы предлагали приезжим следующую задачу: пройти по всем мостам и вернуться в
- 6. дальше Я здесь уже был!
- 7. Задача о Кенигсбергских мостах Пройти по Кенигсбергским мостам, соблюдая заданные условия, нельзя. Прохождение по всем мостам
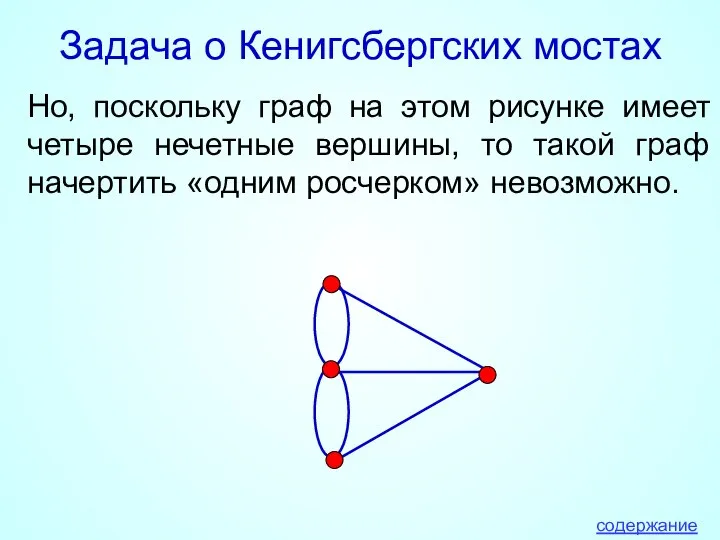
- 8. Задача о Кенигсбергских мостах Но, поскольку граф на этом рисунке имеет четыре нечетные вершины, то такой
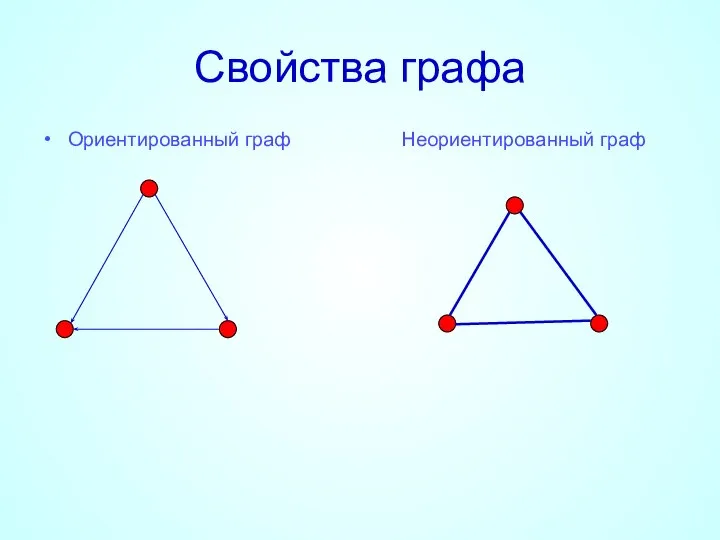
- 9. Свойства графа Ориентированный граф Неориентированный граф
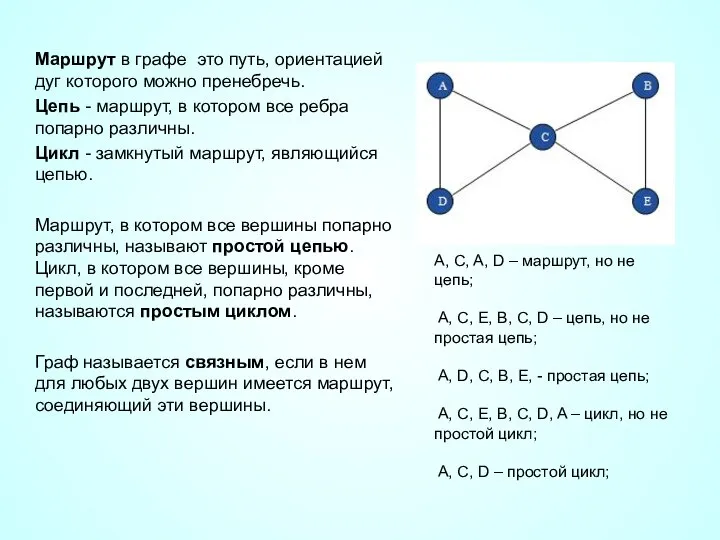
- 10. Маршрут в графе это путь, ориентацией дуг которого можно пренебречь. Цепь - маршрут, в котором все
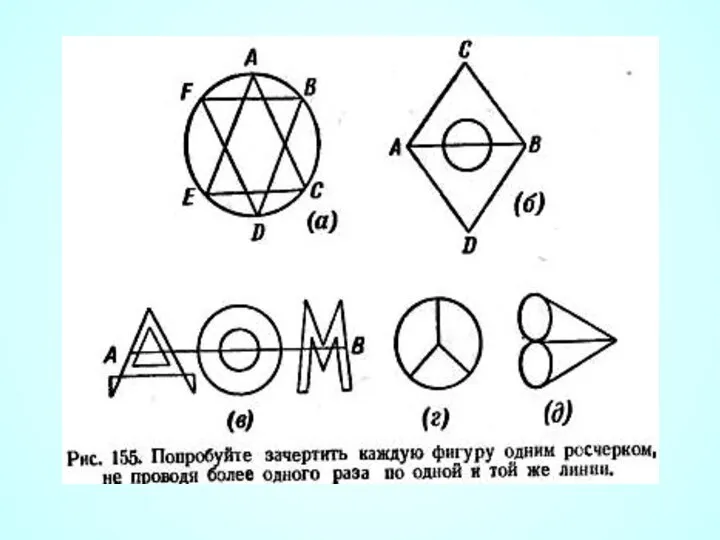
- 11. Одним росчерком Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым. Решая задачу О
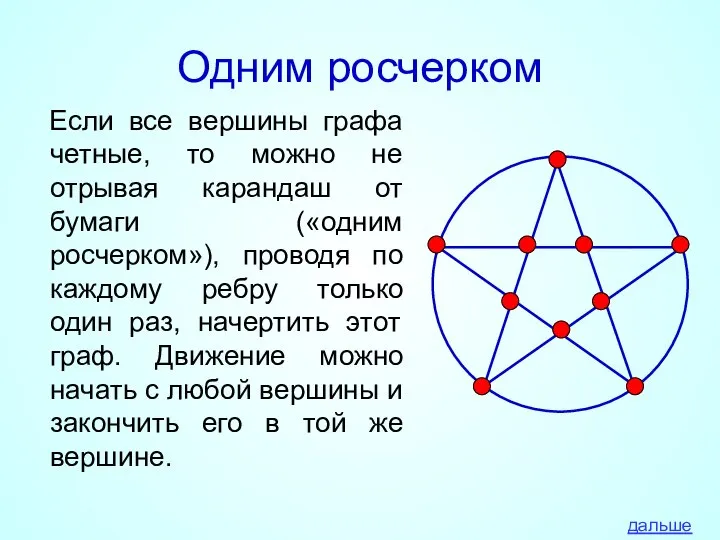
- 12. Одним росчерком Если все вершины графа четные, то можно не отрывая карандаш от бумаги («одним росчерком»),
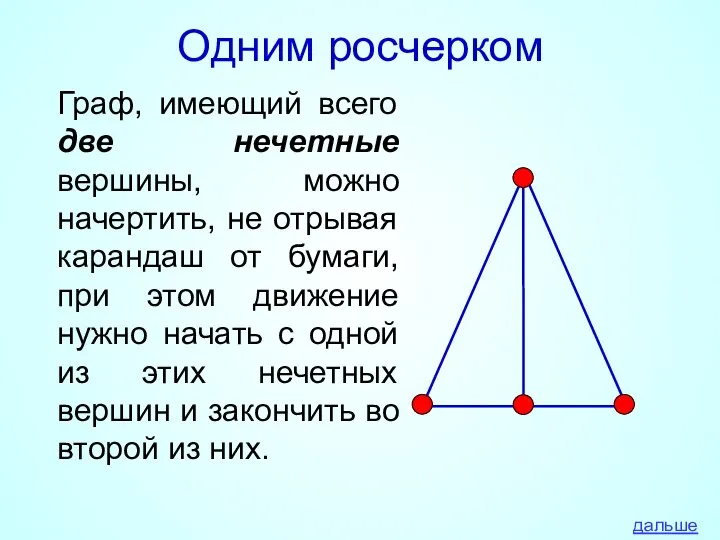
- 13. Одним росчерком Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при
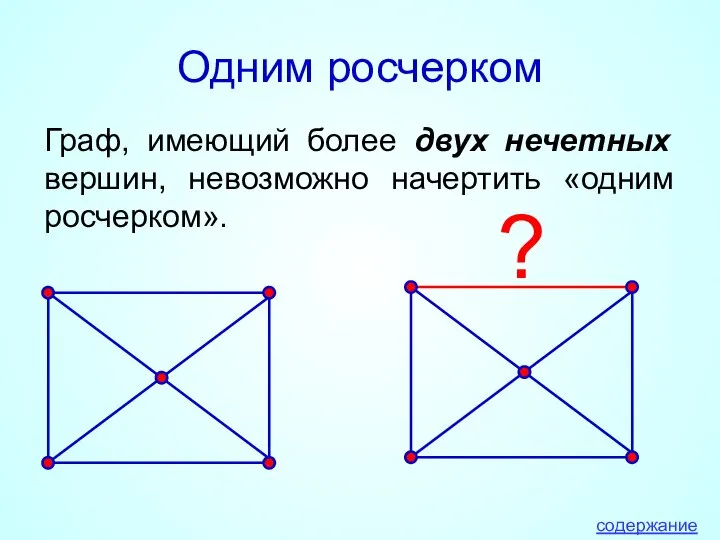
- 14. Одним росчерком Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком». ? содержание
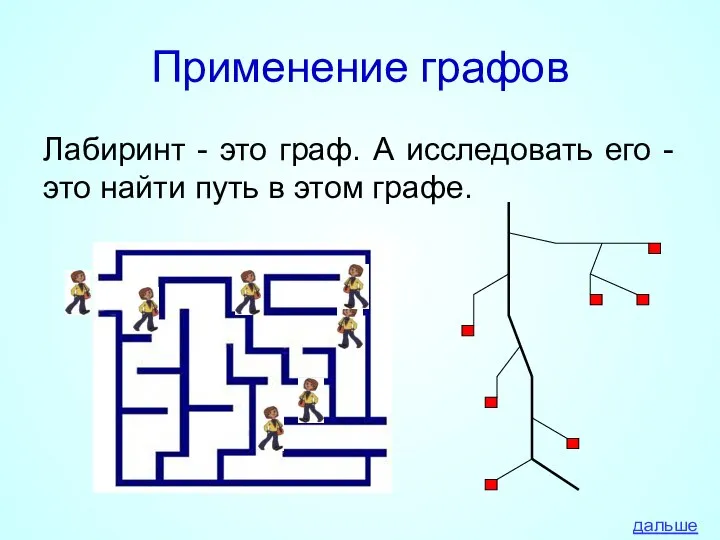
- 16. Применение графов Лабиринт - это граф. А исследовать его - это найти путь в этом графе.
- 18. Первый многосвязный садовый лабиринт был сооружён в 1820-е годы в Чевнинге в Великобритании.
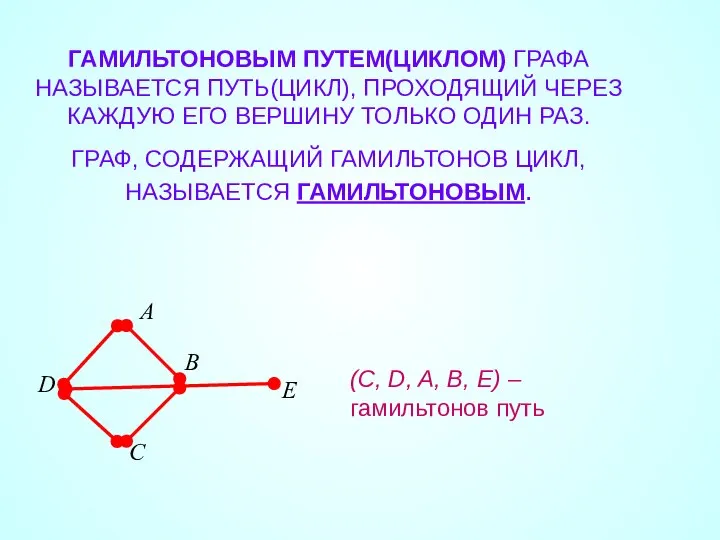
- 19. ГАМИЛЬТОНОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), ПРОХОДЯЩИЙ ЧЕРЕЗ КАЖДУЮ ЕГО ВЕРШИНУ ТОЛЬКО ОДИН РАЗ. ГРАФ, СОДЕРЖАЩИЙ ГАМИЛЬТОНОВ
- 20. В 1857 году ирландский математик Гамильтон предложил игру, названную «Путешествием по додекаэдру». Игра сводилась к обходу
- 21. Выводы Графы – это замечательные математические объекты, с помощью, которых можно решать математические, экономические и логические
- 22. ТЕОРЕМА В ГРАФЕ СУММА СТЕПЕНЕЙ ВСЕХ ЕГО ВЕРШИН – ЧИСЛО ЧЕТНОЕ, РАВНОЕ УДВОЕННОМУ ЧИСЛУ РЕБЕР ГРАФА:
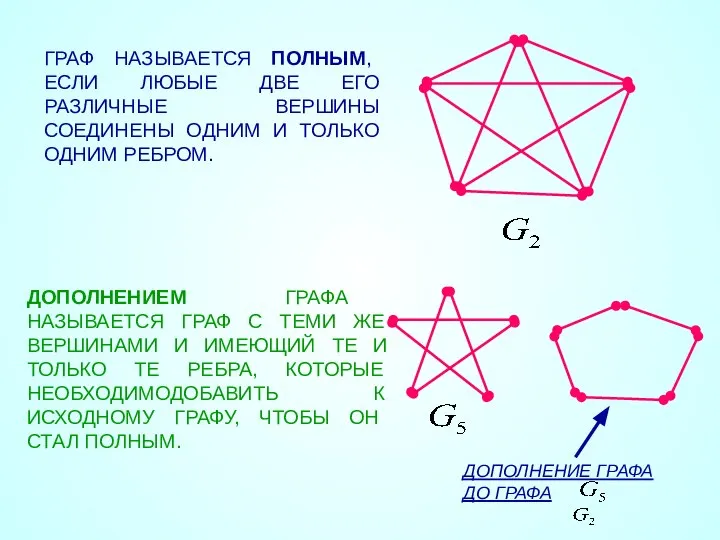
- 23. ГРАФ НАЗЫВАЕТСЯ ПОЛНЫМ, ЕСЛИ ЛЮБЫЕ ДВЕ ЕГО РАЗЛИЧНЫЕ ВЕРШИНЫ СОЕДИНЕНЫ ОДНИМ И ТОЛЬКО ОДНИМ РЕБРОМ. ДОПОЛНЕНИЕМ
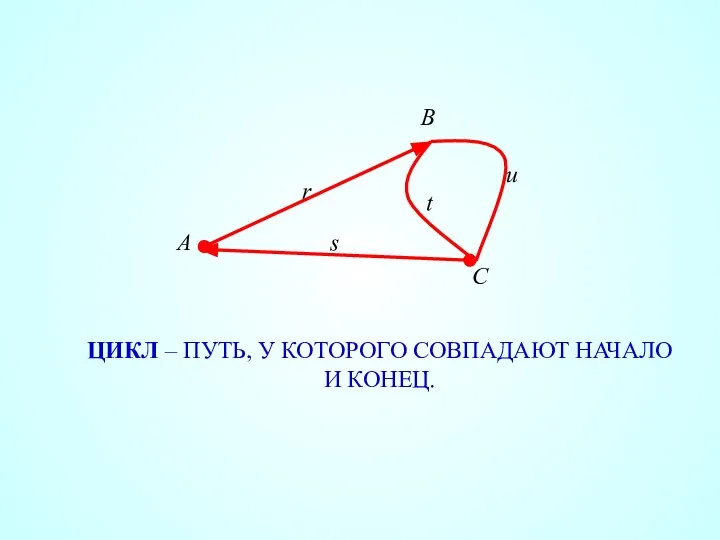
- 24. ЦИКЛ – ПУТЬ, У КОТОРОГО СОВПАДАЮТ НАЧАЛО И КОНЕЦ.
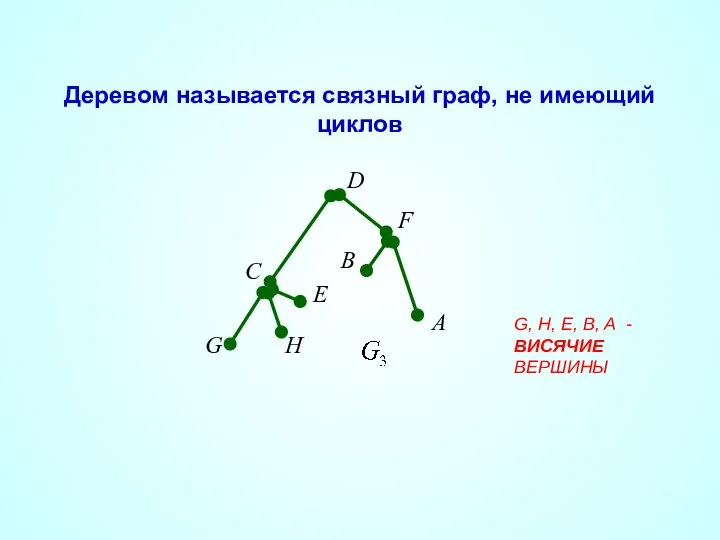
- 25. G, H, E, B, A - ВИСЯЧИЕ ВЕРШИНЫ Деревом называется связный граф, не имеющий циклов
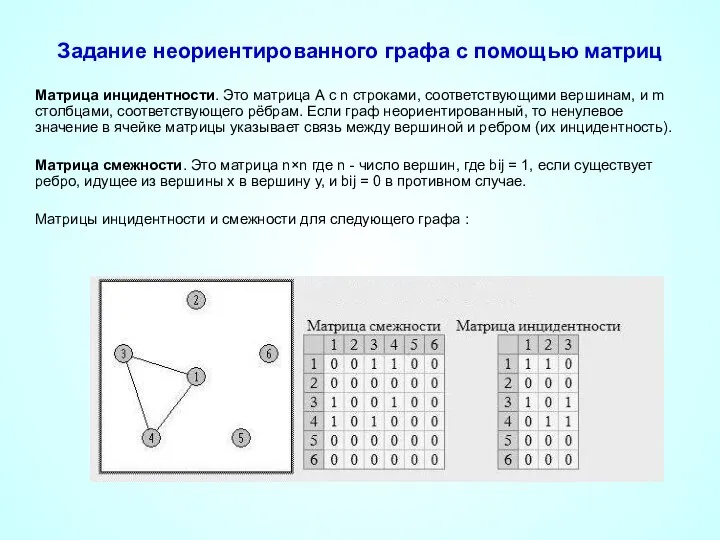
- 26. Задание неориентированного графа с помощью матриц Матрица инцидентности. Это матрица А с n строками, соответствующими вершинам,
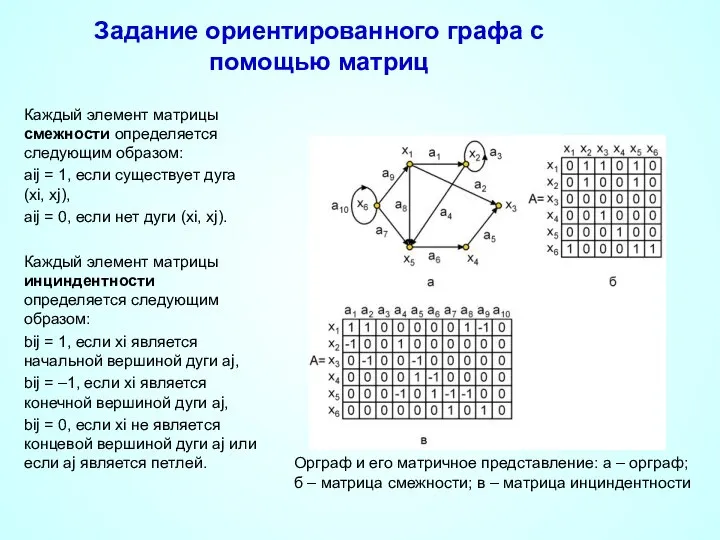
- 27. Задание ориентированного графа с помощью матриц Каждый элемент матрицы смежности определяется следующим образом: aij = 1,
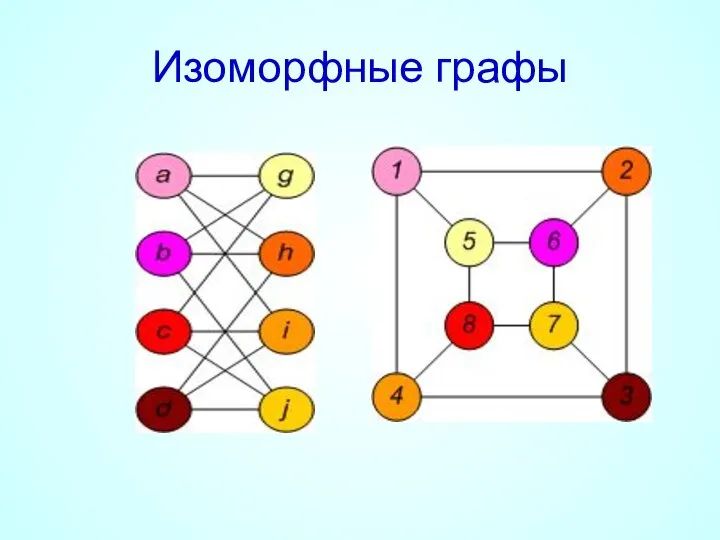
- 28. Изоморфные графы
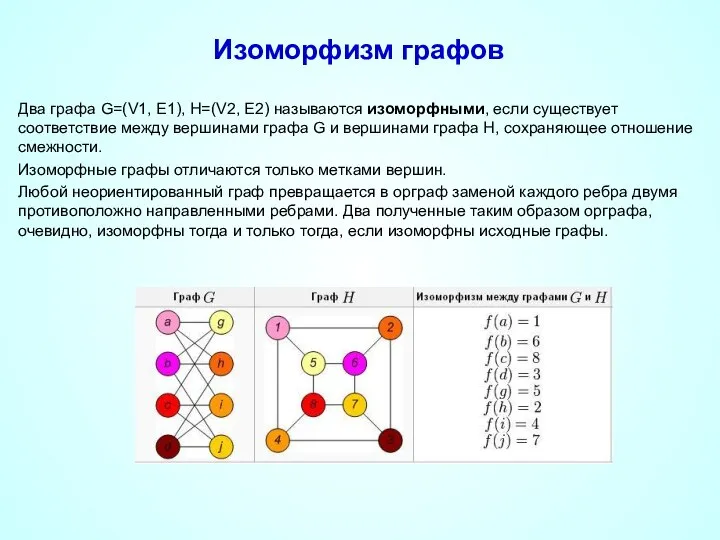
- 29. Изоморфизм графов Два графа G=(V1, E1), H=(V2, E2) называются изоморфными, если существует соответствие между вершинами графа
- 30. Применение графов Использует графы и дворянство. На рисунке приведена часть генеалогического дерева знаменитого дворянского рода Л.
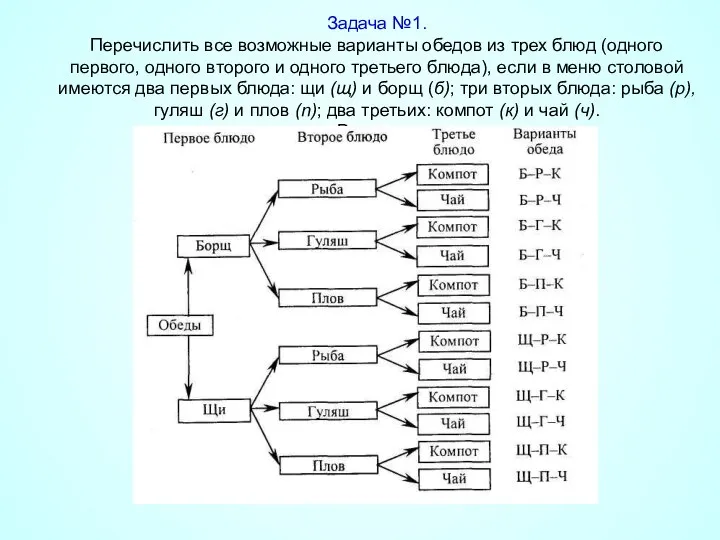
- 31. Задача №1. Перечислить все возможные варианты обедов из трех блюд (одного первого, одного второго и одного
- 32. Применение графов Задача 1: Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал
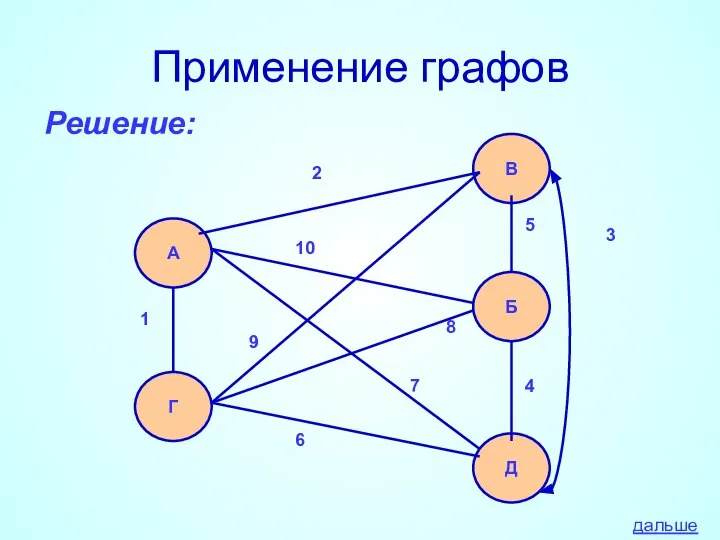
- 33. Применение графов Решение: А Г В Б Д 1 2 3 4 5 6 7 8
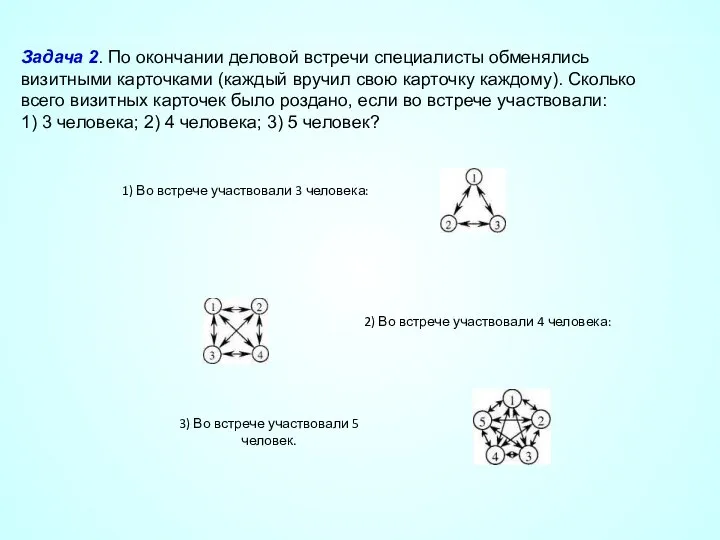
- 34. Задача 2. По окончании деловой встречи специалисты обменялись визитными карточками (каждый вручил свою карточку каждому). Сколько
- 35. Логические задачи
- 36. Задача «Подружки» У трёх подружек - Ксюши, Насти и Оли - новогодние карнавальные костюмы белого, фиолетового
- 37. 1. Костюм и шапочка Насти одного цвета. 2. Костюм и шапочка Ксюши не фиолетового цвета. 3.
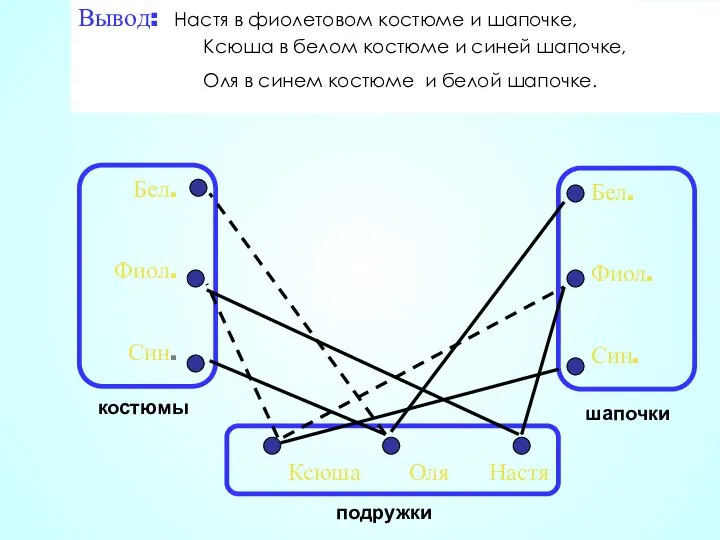
- 38. Вывод: Настя в фиолетовом костюме и шапочке, Ксюша в белом костюме и синей шапочке, Оля в
- 39. Задача «Учительницы» Три учительницы - Ирина Васильевна, Дарья Михайловна и Софья Петровна - преподают химию, биологию
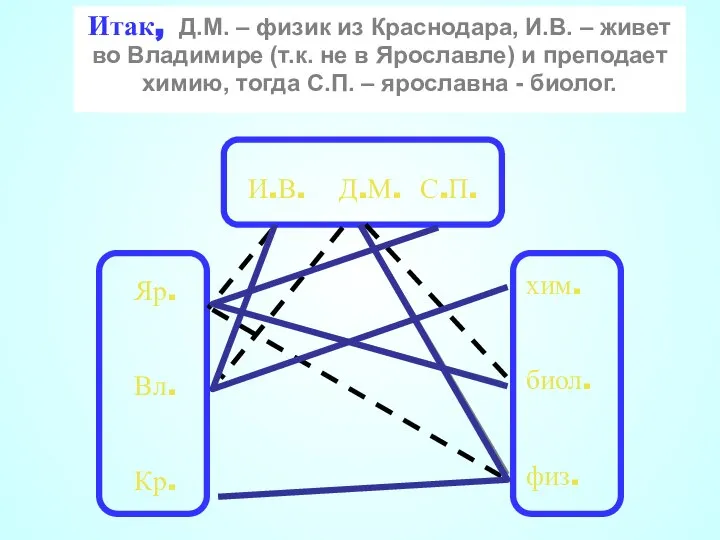
- 40. И.В. Д.М. С.П. Яр. Вл. Кр. хим. биол. физ. 1. И.В. работает не в Ярославле, а
- 41. Итак: Д.М. – физик из Краснодара, И.В. – живет во Владимире (т.к. не в Ярославле) и
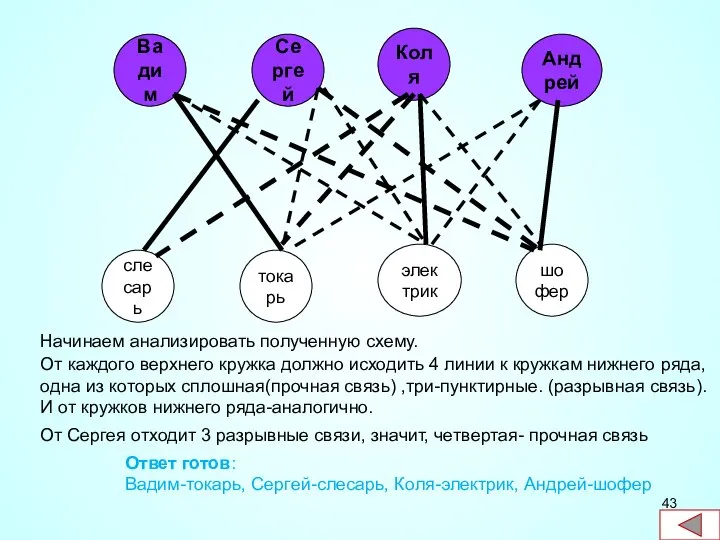
- 42. В одном дворе живут четыре друга. Вадим и шофер старше Сергея, Николай и слесарь занимаются боксом,
- 43. Вадим Коля Сергей Андрей слесарь токарь электрик шофер Начинаем анализировать полученную схему. От каждого верхнего кружка
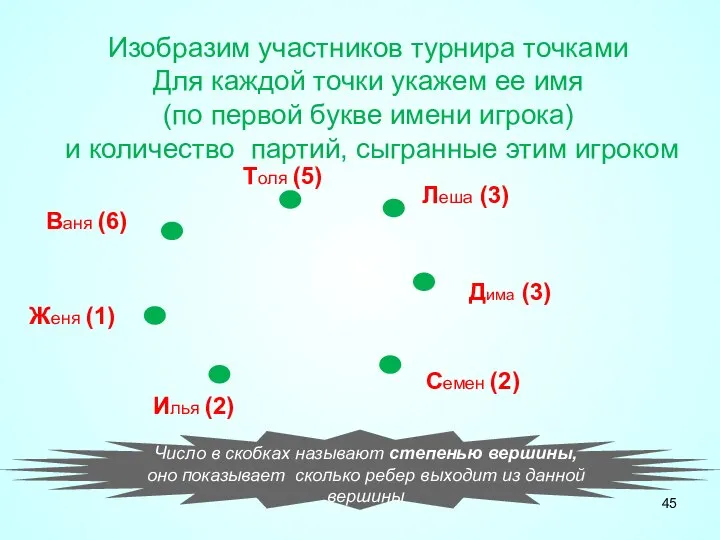
- 44. Известно, что в настоящий момент: Ваня сыграл шесть партий; Толя сыграл пять партий; Леша и Дима
- 45. Число в скобках называют степенью вершины, оно показывает сколько ребер выходит из данной вершины Ваня (6)
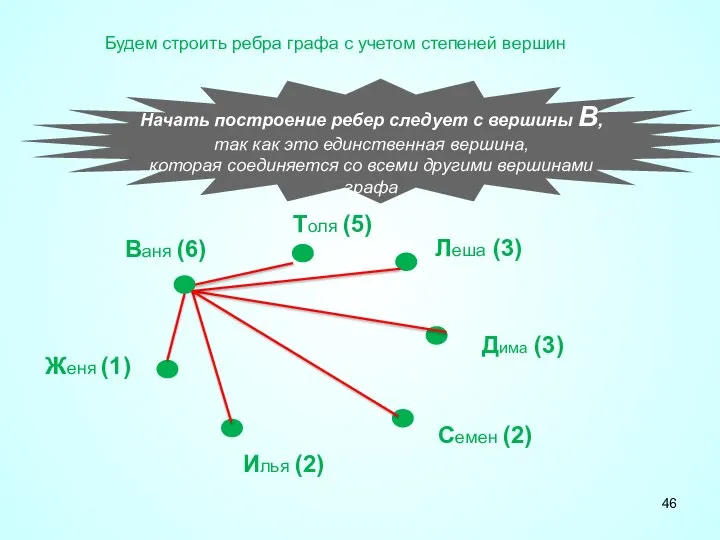
- 46. Начать построение ребер следует с вершины В, так как это единственная вершина, которая соединяется со всеми
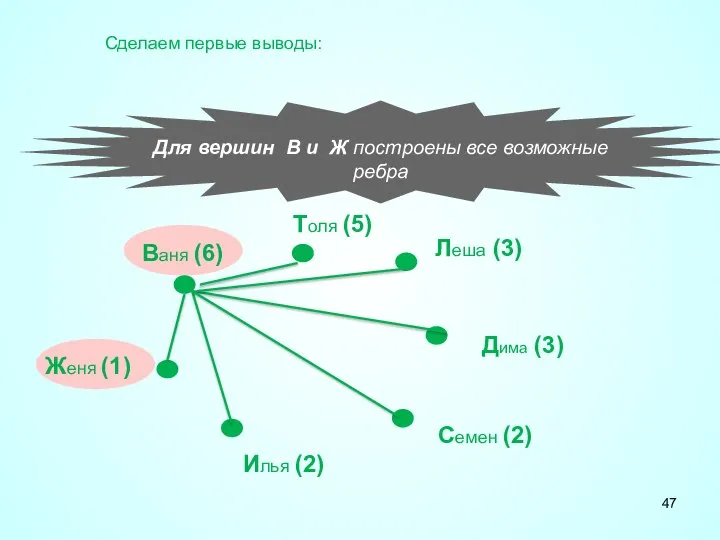
- 47. Для вершин В и Ж построены все возможные ребра Ваня (6) Толя (5) Леша (3) Дима
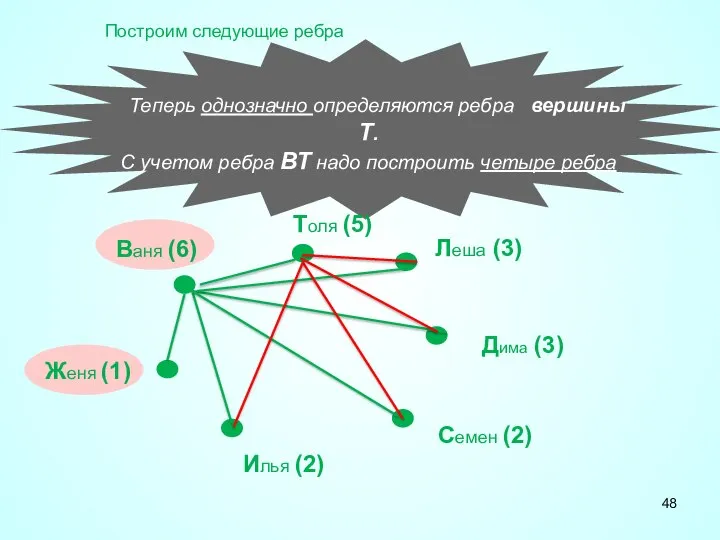
- 48. Теперь однозначно определяются ребра вершины Т. С учетом ребра ВТ надо построить четыре ребра Ваня (6)
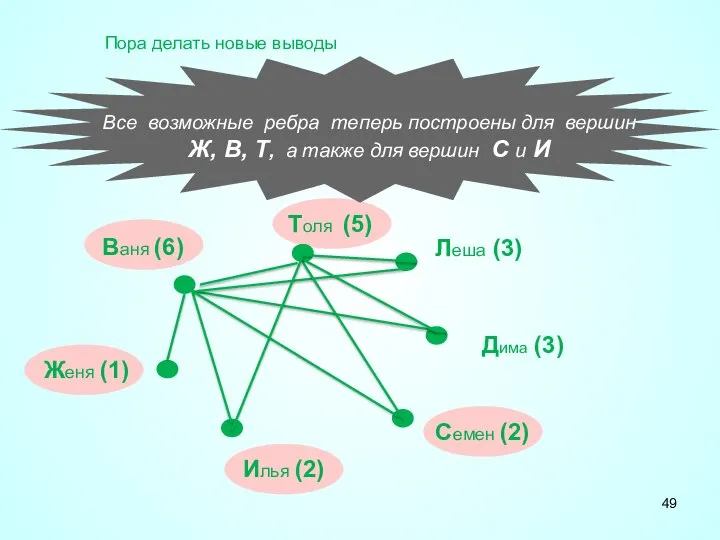
- 49. Все возможные ребра теперь построены для вершин Ж, В, Т, а также для вершин С и
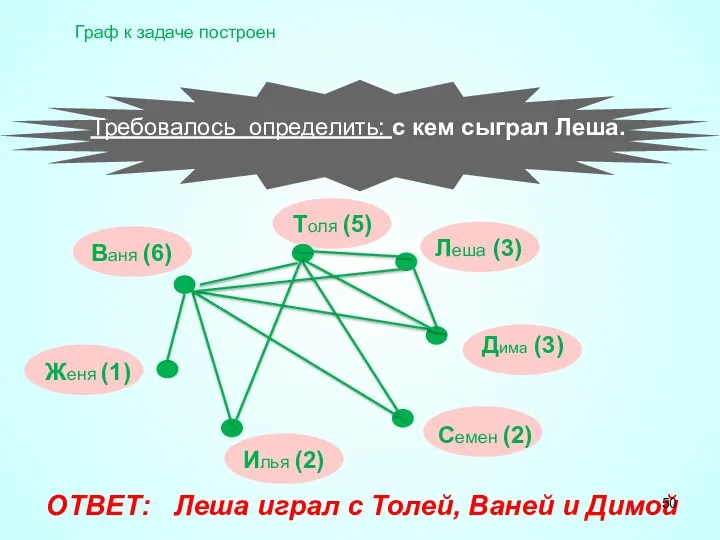
- 50. ОТВЕТ: Леша играл с Толей, Ваней и Димой Ваня (6) Толя (5) Леша (3) Дима (3)
- 52. Скачать презентацию


















 Производная функции. Геометрический смысл производной
Производная функции. Геометрический смысл производной Расстояние между двумя точками (9 класс)
Расстояние между двумя точками (9 класс) Графики функций. Зачет
Графики функций. Зачет Теорема косинусов
Теорема косинусов Конические сечения и их применения в технике
Конические сечения и их применения в технике Понятие логарифма
Понятие логарифма Презентация на тему Квадратный корень. Арифметический квадратный корень
Презентация на тему Квадратный корень. Арифметический квадратный корень  Отношения. Функции
Отношения. Функции Функции и их графики
Функции и их графики Правильные многоугольники
Правильные многоугольники Счет сотнями до 1000
Счет сотнями до 1000 Соотношение между гипотенузой и катетами прямоугольного треугольника
Соотношение между гипотенузой и катетами прямоугольного треугольника Перпендикуляр и наклонная. Теорема о трёх перпендикулярах
Перпендикуляр и наклонная. Теорема о трёх перпендикулярах Действие над векторами в пространстве
Действие над векторами в пространстве Перпендикулярность прямых в пространстве
Перпендикулярность прямых в пространстве Окружность и длина окружности
Окружность и длина окружности Фундаментальные и прикладные исследования в метрологии
Фундаментальные и прикладные исследования в метрологии Множественные связи. Порядковые и категоризованные переменные
Множественные связи. Порядковые и категоризованные переменные Графический метод решения уравнений с параметром
Графический метод решения уравнений с параметром Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве Методы параллельных вычислений
Методы параллельных вычислений Технология подготовки учащихся к овладению функционально-графическими методами решения задач с параметрами. (Занятие №3)
Технология подготовки учащихся к овладению функционально-графическими методами решения задач с параметрами. (Занятие №3) Сводка и группировка данных статистического наблюдения
Сводка и группировка данных статистического наблюдения Интервальные оценки
Интервальные оценки Проецирование
Проецирование ГИА - 2016. Открытый банк заданий по математике. Задача №18
ГИА - 2016. Открытый банк заданий по математике. Задача №18 Решение задач ЕГЭ
Решение задач ЕГЭ Из истории геометрии
Из истории геометрии