Содержание
- 2. МНОГОЧЛЕНЫ НАД ЧИСЛОВЫМИ ПОЛЯМИ ЛЕКЦИЯ 9 Доцент Мартынова Т.А.
- 3. § 1. Многочлены над полем комплексных чисел Основными задачами этого раздела являются рассмотрение вопросов: Основная теорема
- 4. 3. Кубические уравнения x3 + px + q = 0 (8) u + v = x0
- 5. 3. Кубические уравнения x3 + px + q = 0 (8) u + v = x0
- 6. 3. Кубические уравнения x3 + px + q = 0 (8) u + v = x0
- 7. 3. Кубические уравнения z = x – a/3 (7) x3 + px + q = 0
- 8. 3. Кубические уравнения Пример 4. Решить уравнение x3 – 12x + 16 = 0. ◘ Здесь
- 9. 3. Кубические уравнения Пример 5. Решить: z3 – 9z2 + 21z – 5 = 0. ◘
- 10. 3. Кубические уравнения x3 + px + q = 0 (8) u + v = x0
- 11. 3. Кубические уравнения 1. Δ = 0, 2. Δ > 0, 3. Δ 1. Если Δ
- 12. 3. Кубические уравнения Обращаясь к формулам (16), получаем x1= u1 + v1 = 3q/p, x2= x3=
- 13. 3. Кубические уравнения Таким образом при Δ>0 уравнение (8) имеет только один действительный корень, x1=u1+v1, а
- 14. 3. Кубические уравнения С помощью некоторых преобразований получаем X1 = u1+v1 = 2|3√r |cosϕ/3, X2 =
- 15. 3. Кубические уравнения Недостатком формулы Кордано является то, что часто рациональные корни она представляет в иррациональном
- 16. 4. Уравнения четвёртой степени Дано уравнение четвёртой степени: x4 + ax3 + bx2 + cx +
- 17. 4. Уравнения четвёртой степени К обеим частям теперь прибавим: Тогда: Теперь число y подбирается так, чтобы
- 18. 4. Уравнения четвёртой степени Пусть y0 – корень уравнения (19). Тогда (18) приводится к виду: для
- 19. 4. Уравнения четвёртой степени Пример 6. Решить: x4 – 2x3 + 2x2 + 4x – 8
- 20. 4. Уравнения четвёртой степени Составляем кубическую резольвенту уравнения (21): Непосредственно видно, что одним из корней последнего
- 22. Скачать презентацию



















 Взаимное расположение двух окружностей
Взаимное расположение двух окружностей Numbers and animals
Numbers and animals Найдите высоту и медиану треугольника
Найдите высоту и медиану треугольника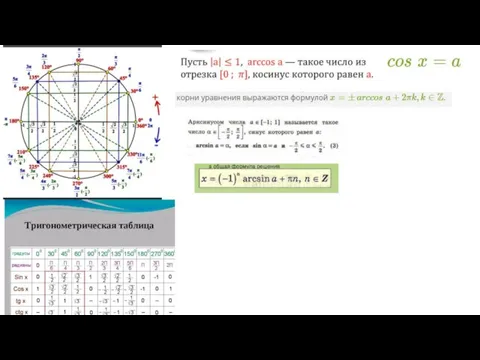 Тригонометрические неравенства
Тригонометрические неравенства Презентация на тему Устный счёт 1 класс
Презентация на тему Устный счёт 1 класс  Формулы сокращенного умножения. Формулы суммы и разности кубов двух выражений (изучение нового материала)
Формулы сокращенного умножения. Формулы суммы и разности кубов двух выражений (изучение нового материала) Классификация треугольников
Классификация треугольников Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента Множественная регрессия и корреляция
Множественная регрессия и корреляция Вычисление производных с помощью правил дифференцирования
Вычисление производных с помощью правил дифференцирования Reshenie_sistem_logicheskikh_uravneniy_vse_metody
Reshenie_sistem_logicheskikh_uravneniy_vse_metody Поле чудес. 3 класс
Поле чудес. 3 класс Понятие функции
Понятие функции Метрология. Основные понятия
Метрология. Основные понятия Преобразование чисел, полученных при измерении мерами стоимости, длины, массы
Преобразование чисел, полученных при измерении мерами стоимости, длины, массы Непрерывный интервальный ряд распределения. Гистограмма
Непрерывный интервальный ряд распределения. Гистограмма Разработка обучающей программы по нахождению элементов треугольника
Разработка обучающей программы по нахождению элементов треугольника Буквенные выражения
Буквенные выражения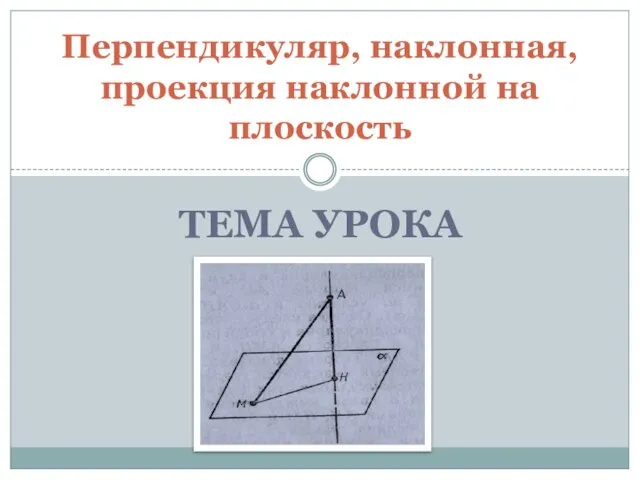 Презентация на тему Перпендикуляр, наклонная, проекция наклонной на плоскость
Презентация на тему Перпендикуляр, наклонная, проекция наклонной на плоскость  Координатная плоскость. Мультстудия
Координатная плоскость. Мультстудия Дифференциальные и разностные уравнения
Дифференциальные и разностные уравнения Луч. Отрезок. Путешествие точки
Луч. Отрезок. Путешествие точки Тема урока: « Закрепление вычислительных навыков, сравнения чисел. Нумерация в пределах 100.»
Тема урока: « Закрепление вычислительных навыков, сравнения чисел. Нумерация в пределах 100.» Сравнение предметов. Счет до 5
Сравнение предметов. Счет до 5 Дробные числительные
Дробные числительные Объем конуса и цилиндра
Объем конуса и цилиндра Презентация на тему Квадратное уравнение и его корни
Презентация на тему Квадратное уравнение и его корни  Оптимізація об’єктів в статичних режимах. Метод множників лагранжа. (Лабораторна робота 1)
Оптимізація об’єктів в статичних режимах. Метод множників лагранжа. (Лабораторна робота 1)