Функция y = sinx её свойства и график

Цель:
Изучить функцию y = sinx
Задачи:
1. Изучить свойства функции у = sin x.
2. Уметь применять свойства функции у = sin x и читать график.
3. Формировать практические навыки построения графика функции у = sin x на основе изученного теоретического материала.
4. Закрепить понятия с помощью выполнения заданий.

Функция y = sin x определена на всей числовой прямой, и множеством её значений является отрезок [−1;1].
Следовательно, график этой функции расположен в полосе между прямыми y= −1 и y=1.
Так как функция y = sin x периодическая с периодом 2π, то достаточно построить её график на каком-нибудь промежутке длиной 2π, например, на отрезке 0≤x≤2π, тогда на промежутках, получаемых сдвигами выбранного отрезка на 2πn, n∈Z, график будет таким же.

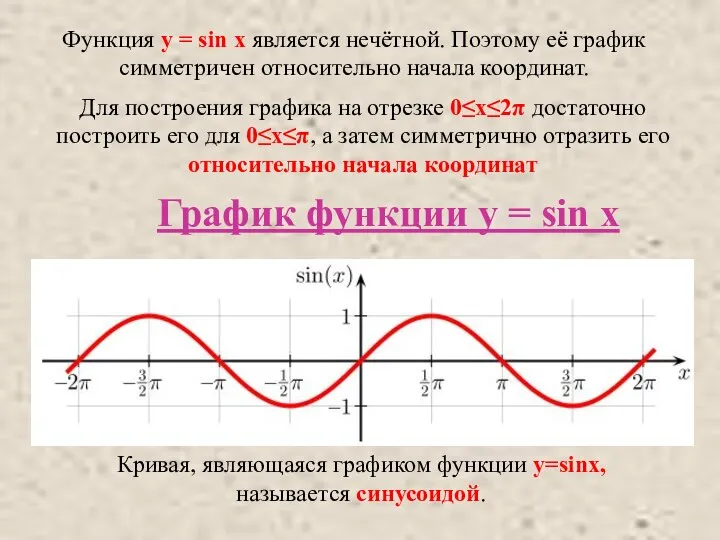
Функция y = sin x является нечётной. Поэтому её график симметричен относительно начала координат.
Для построения графика на отрезке 0≤x≤2π достаточно построить его для 0≤x≤π, а затем симметрично отразить его относительно начала координат
График функции y = sin x
Кривая, являющаяся графиком функции y=sinx, называется синусоидой.

Свойства функции y = sin x
1. Область определения — множество R всех действительных чисел. D(y) = (-∞; + ∞)
2. Множество значений Е(у) = [−1;1]
3. Функция периодическая с периодом T= 2π.
4. Функция нечётная sin(-x) = -sin x
(график симметричен относительно начала координат).
5. Функция ограничена и сверху, и снизу.
6. Функция y=sinx принимает:
- значение, равное 0, при x=πn, n∈Z;
- наибольшее значение, равное 1, при x=π/2+2πn, n∈Z;
- наименьшее значение, равное −1, при x=−π/2+2πn, n∈Z;

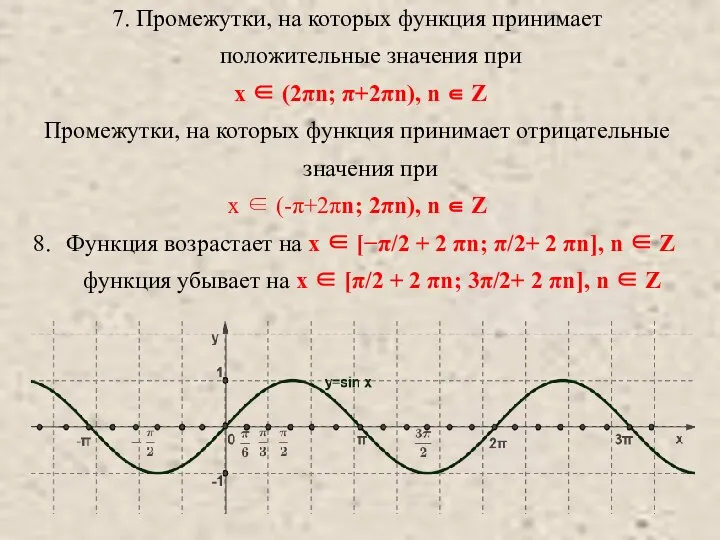
7. Промежутки, на которых функция принимает положительные значения при
x ∈ (2πn; π+2πn), n ∈ Z
Промежутки, на которых функция принимает отрицательные значения при
x ∈ (-π+2πn; 2πn), n ∈ Z
Функция возрастает на x ∈ [−π/2 + 2 πn; π/2+ 2 πn], n ∈ Z
функция убывает на x ∈ [π/2 + 2 πn; 3π/2+ 2 πn], n ∈ Z

Решение задач
Задача 1.
Найти наибольшее и наименьшее значение функции
y=sin t на отрезке [-π/6;π/2]
Функция монотонно возрастает на указанном промежутке, значит, наибольшее значение принимает на правом конце отрезка у(π/2)=1, а наименьшее значение принимает на его левом конце у(π/6) = -1/2
Решение

Задача 2.
Найти наибольшее и наименьшее значение функции
y=sin t на отрезке [-π/4; -π/6]
Решение
Функция монотонно возрастает на указанном промежутке, значит, наибольшее значение принимает на правом конце отрезка у(-π/6) = -1/2, а наименьшее значение принимает на его левом конце у(-π/4) = -√2/2

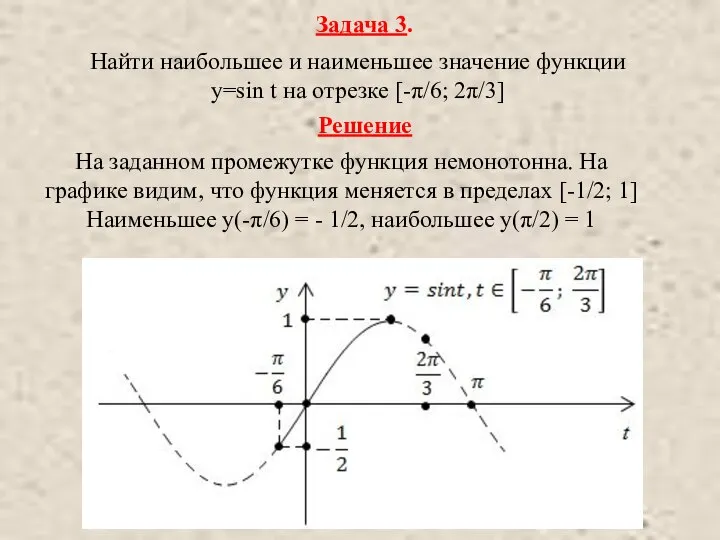
Задача 3.
Найти наибольшее и наименьшее значение функции
y=sin t на отрезке [-π/6; 2π/3]
Решение
На заданном промежутке функция немонотонна. На графике видим, что функция меняется в пределах [-1/2; 1] Наименьшее y(-π/6) = - 1/2, наибольшее у(π/2) = 1

Задача 4.
Построить график функции
Построим график функции y = sin t. В силу периодичности достаточно будет рассмотреть график на участке [0;2π]. Для получения искомого графика кривую y = sin t необходимо сдвинуть на π/6 вправо по оси х
Решение

Задача 5.
Найти наибольшее и наименьшее значение функции
на отрезке [0; π/2]
Решение

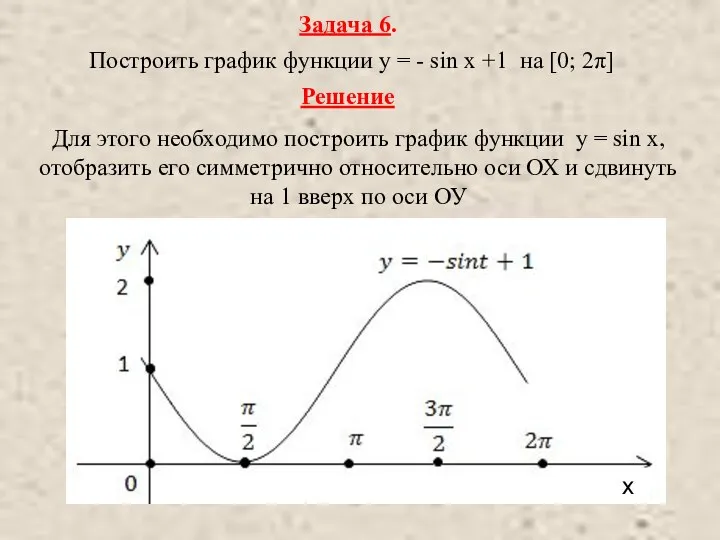
Задача 6.
Построить график функции y = - sin x +1 на [0; 2π]
Решение
Для этого необходимо построить график функции y = sin x, отобразить его симметрично относительно оси ОХ и сдвинуть на 1 вверх по оси ОУ
х

Задача 7.
Найти число решений уравнения
Решение
Построим в одних координатных осях графики функций
Видно, что графики функций пересекаются в двух точках. Значит всего уравнение имеет два решения.

Задача 8.
Решить уравнение
Построим в одних координатных осях графики функций
На рисунке видно, что построенные графики функций имеют только одну общую точку с абсциссой
Решение

у
2
= sinx + 2;
у
3
= sinx - 2
Задания для самостоятельного решения
Постройте графики функций
1) у = sinx + 1;
2) у = sinx – 1;
3) у = sin (x + π/2)
4) у = sin (x – π/3)
5) Найти наибольшее и наименьшее значение функции y=sin (x) на отрезке [0; 4π/3]
Найдите область значений функции:
 



