Слайд 2Замечательные пределы, эквивалентные функции
Первый замечательный предел:
Бесконечно малые в точке х0

функции f(x) и g(x) называются эквивалентными, если
Обозначают: f(x) ~ g(x).
При вычислении пределов функцию можно заменять на эквивалентную (если эта функция является множителем, а не слагаемым).
Слайд 3Примеры эквивалентных функций (в точке х0 =0)
Второй замечательный предел:

Слайд 6Исследование функции
проводится по следующей схеме
1. Область определения функции D(f).
Множество значений функции

E(f).
2. Четность, нечетность, периодичность
f(х) – четная ⇔ ∀х, (−х)∈D(f) f(− х) = f(х)
(график симметричен относительно оси Оу)
f(х) – нечетная ⇔ ∀х, (−х)∈D(f) f(− х) = − f(х)
(график симметричен относительно начала координат)
Если ни одно условие не выполняется, то
f(х) – функция общего вида.
Слайд 7f(х) – периодическая с периодом Т ⇔
∀х, (х−Т), (х+Т) ∈D(f) f(х)

= f(х−Т) = f(х+Т)
(определяется только для тригонометрических функций)
3. Точки пересечения графика с осями координат
Пересечение с Оу существует, если х = 0 ∈D(f), точка пересечения (0, f(0))
(график пересекает Оу не более чем в одной точке).
Пересечение с Ох определяется в результате решения уравнения: f(х) = 0.










 Математика. Часть 1
Математика. Часть 1 Практико-ориентированные задания. ОГЭ, открытый банк заданий ФИПИ
Практико-ориентированные задания. ОГЭ, открытый банк заданий ФИПИ Понятие многогранника. Призма
Понятие многогранника. Призма Евклидова геометрия
Евклидова геометрия 5b6b504ca82342859c8bde10a1b9f03b
5b6b504ca82342859c8bde10a1b9f03b Построение угла заданной величины
Построение угла заданной величины Математический диктант
Математический диктант Математический диктант по теме: Дроби. 6 класс
Математический диктант по теме: Дроби. 6 класс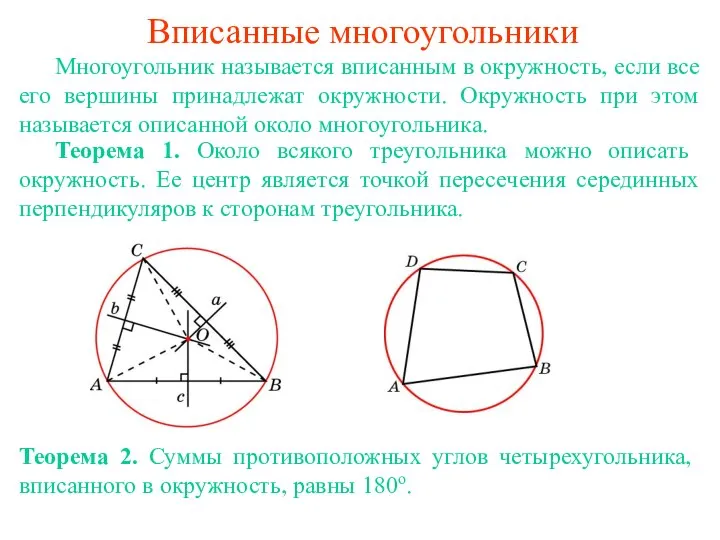 Вписанные и описанные многоугольники
Вписанные и описанные многоугольники Производные функции нескольких переменных (часть 1)
Производные функции нескольких переменных (часть 1) Задачи на максимум и минимум. 11 класс
Задачи на максимум и минимум. 11 класс КВН Знакомьтесь: геометрия
КВН Знакомьтесь: геометрия Геро́н Александри́йский
Геро́н Александри́йский Линейная алгебра. Определители
Линейная алгебра. Определители математика дз
математика дз Случайные величины и их распределения
Случайные величины и их распределения Применение производной для исследования функций на монотонность
Применение производной для исследования функций на монотонность Функции многих переменных: частные производные, дифференциалы. Лекция 2
Функции многих переменных: частные производные, дифференциалы. Лекция 2 Устный счёт. Деление на двузначное число
Устный счёт. Деление на двузначное число Прямоугольная система координат
Прямоугольная система координат Многоугольники. 9 класс
Многоугольники. 9 класс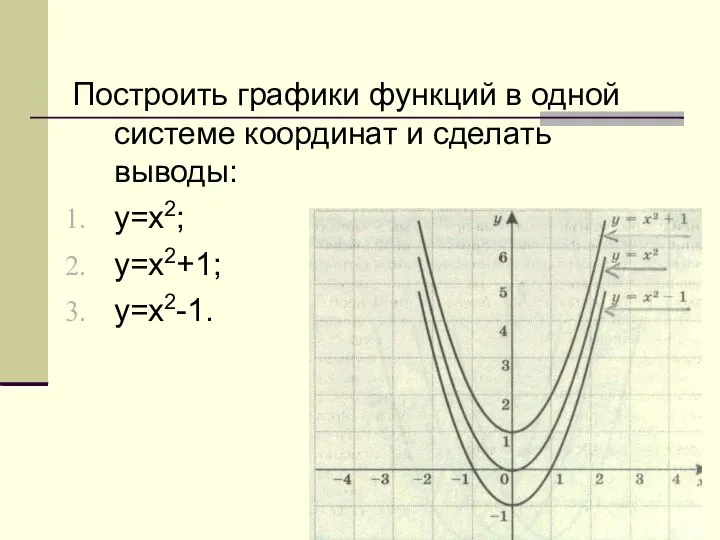 Графики функций в одной системе координат
Графики функций в одной системе координат Математическая викторина. 1 тур. Занимательные задачи
Математическая викторина. 1 тур. Занимательные задачи Геометрические загадки
Геометрические загадки Осевая и центральная симметрии
Осевая и центральная симметрии Устный счет на уроке геометрии в 8 классе
Устный счет на уроке геометрии в 8 классе Презентация на тему Сочетательное свойство сложения
Презентация на тему Сочетательное свойство сложения  Письменное умножение двузначных и трехзначных чисел на однозначное число
Письменное умножение двузначных и трехзначных чисел на однозначное число