1155274

Основні теми розділу
Мимобіжні та паралельні прямі
Паралельність прямої та площини
Паралельність площин
Паралельне проектування та його властивості
Зображення фігур у стереометрії
Методи побудови перерізів многогранників

Мета: вчити
Формулювати означення паралельних і мимобіжних прямих, паралельних прямої і площини, паралельних площин; ознаки паралельності прямих і площин; властивості паралельності прямих і площин.
Класифікувати взаємне розміщення прямих, прямих і площин, площин у просторі.
Знаходити і зображати паралельні прямі, прямі та площини на малюнках, будувати зображення фігур.
Розв’язувати задачі на застосування властивостей та ознак паралельності прямих і площин.
Застосовувати метод слідів та проекцій для побудови перерізів многогранників.

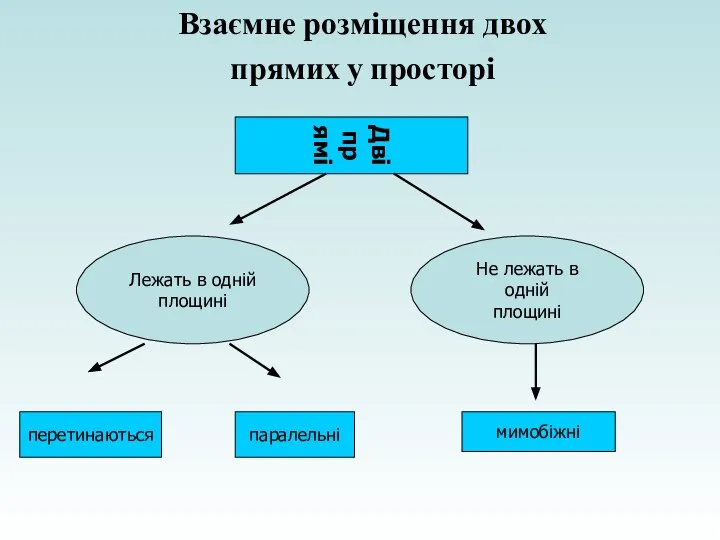
Взаємне розміщення двох
прямих у просторі
Дві прямі
Лежать в одній
площині
Не лежать в одній
площині
перетинаються
паралельні
мимобіжні

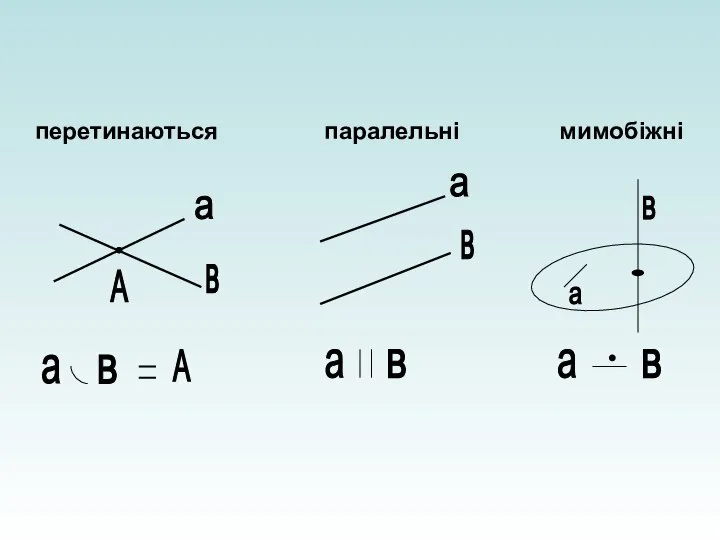
перетинаються паралельні мимобіжні
а
в
А
а
в
а
в
а
в
А
а
в
а
в

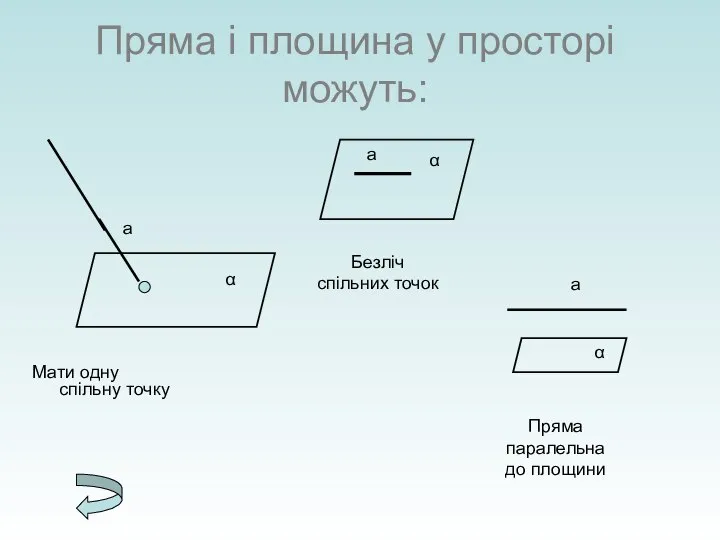
Пряма і площина у просторі можуть:
Мати одну спільну точку
Безліч спільних точок
α
а
а
α
а
α
Пряма паралельна до площини

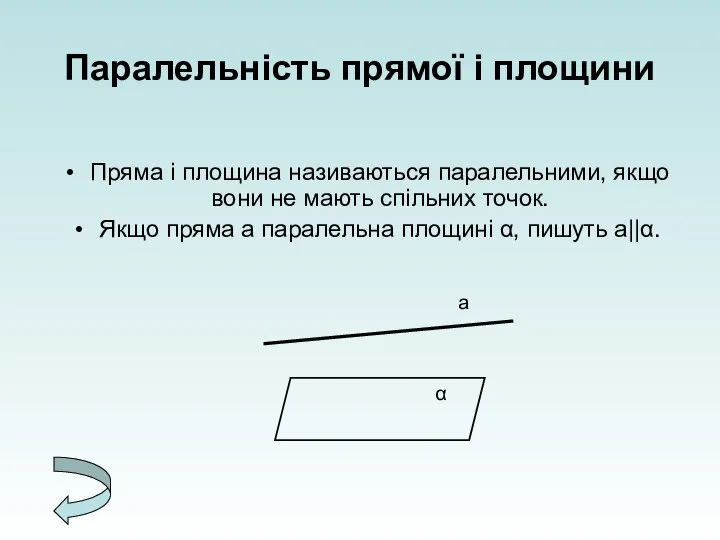
Паралельність прямої і площини
Пряма і площина називаються паралельними, якщо вони не мають спільних точок.
Якщо пряма а паралельна площині α, пишуть а||α.
а
α

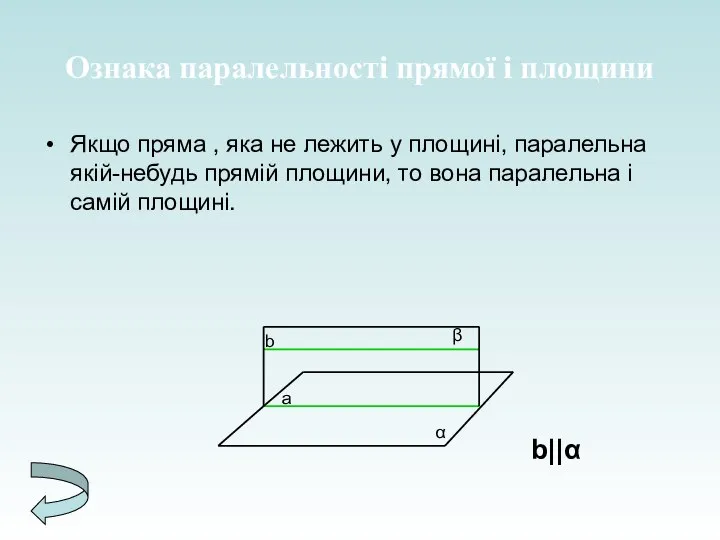
Ознака паралельності прямої і площини
Якщо пряма , яка не лежить у площині, паралельна якій-небудь прямій площини, то вона паралельна і самій площині.
b
a
β
α
b||α

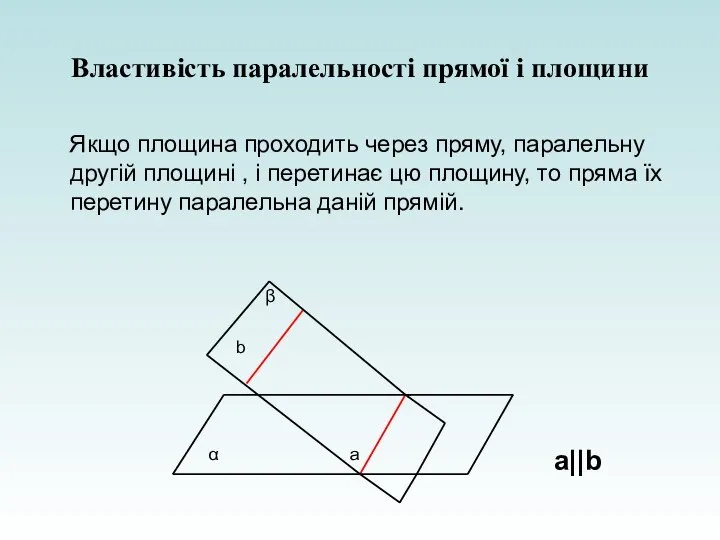
Властивість паралельності прямої і площини
Якщо площина проходить через пряму, паралельну другій площині , і перетинає цю площину, то пряма їх перетину паралельна даній прямій.
α
β
b
a
a||b

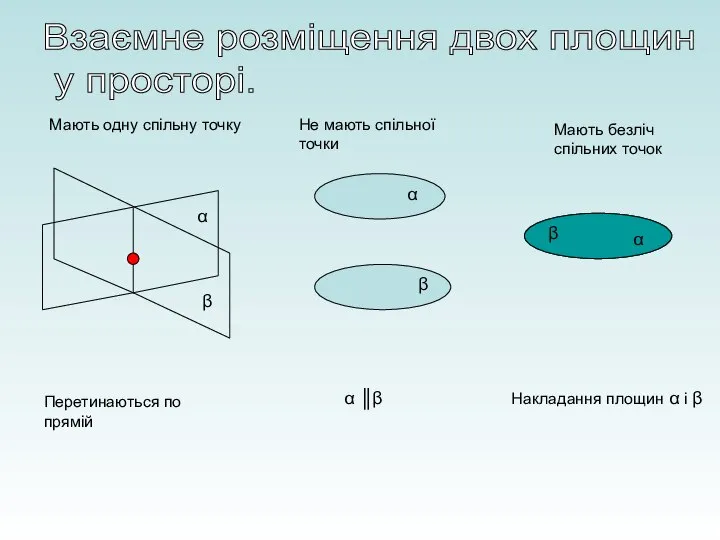
Взаємне розміщення двох площин у просторі.
α
β
α
β
α ║β
α
Мають одну спільну точку
Перетинаються по прямій
Не мають спільної точки
Мають безліч спільних точок
Накладання площин α і β

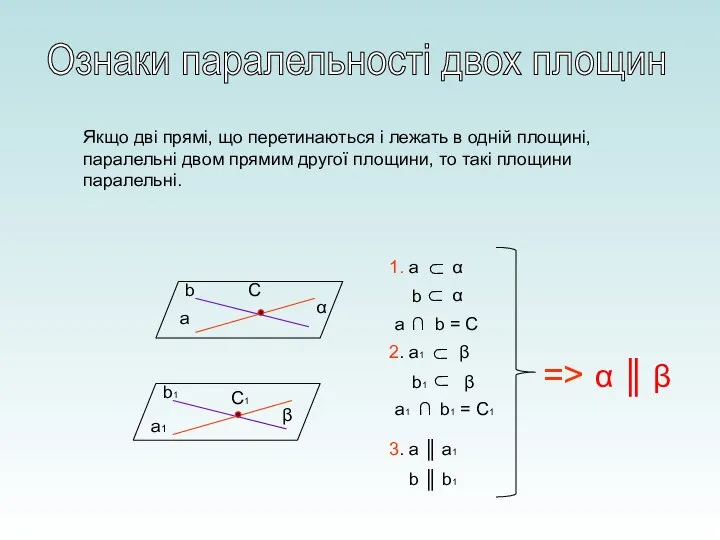
Ознаки паралельності двох площин
Якщо дві прямі, що перетинаються і лежать в одній площині, паралельні двом прямим другої площини, то такі площини паралельні.
a
b
α
a1
b1
β
C
C1
3. a ║ а1
b ║ b1
=> α ║ β

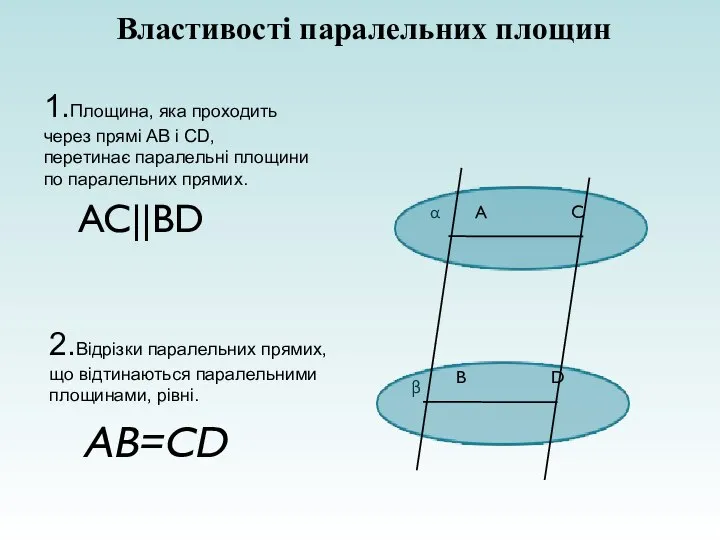
AB=CD
Властивості паралельних площин
2.Відрізки паралельних прямих, що відтинаються паралельними площинами, рівні.
AC||BD
1.Площина, яка проходить через прямі АВ і СD,
перетинає паралельні площини по паралельних прямих.

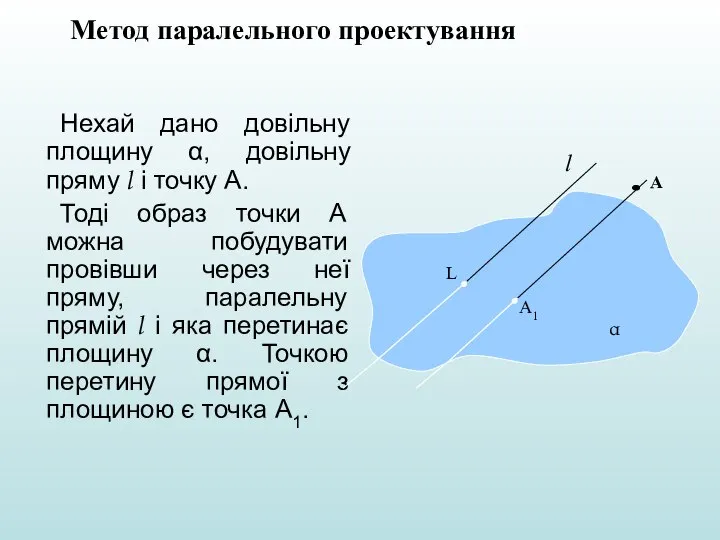
Нехай дано довільну площину α, довільну пряму l і точку А.
Тоді образ точки А можна побудувати провівши через неї пряму, паралельну прямій l і яка перетинає площину α. Точкою перетину прямої з площиною є точка А1.
А1
А
α
l
L
Метод паралельного проектування

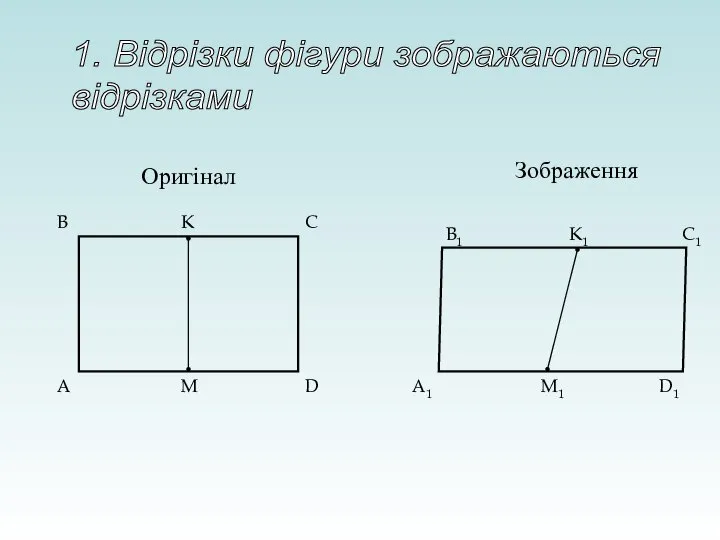
Оригінал
Зображення
K
M
A
B
C
D
B1
A1
D1
C1
K1
M1
1. Відрізки фігури зображаються
відрізками

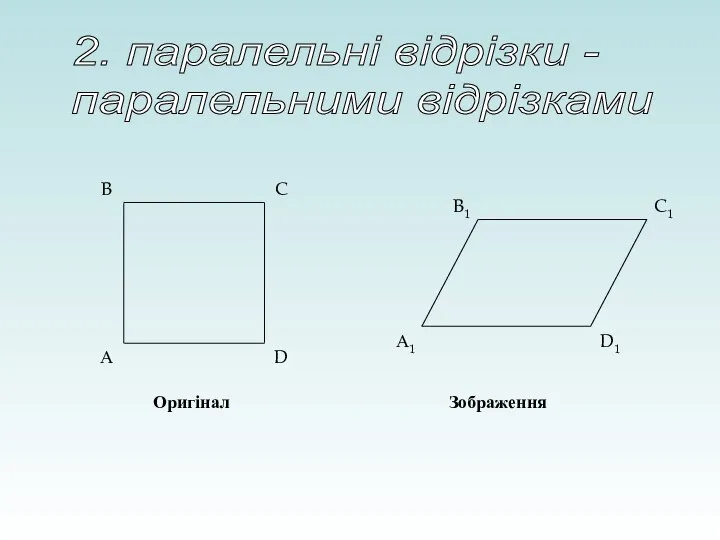
А
B
C
D
А1
B1
C1
D1
Оригінал
Зображення
2. паралельні відрізки -
паралельними відрізками

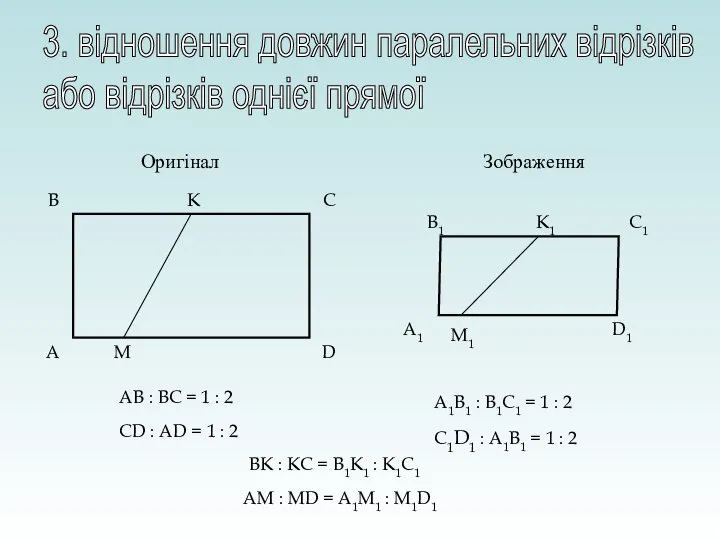
C
B
D
A
C1
B1
D1
A1
Оригінал
Зображення
AB : BC = 1 : 2
A1B1 : B1C1 = 1 : 2
CD : AD = 1 : 2
C1D1 : A1B1 = 1 : 2
BK : KC = B1K1 : K1C1
K
M
K1
M1
AM : MD = A1M1 : M1D1
3. відношення довжин паралельних відрізків
або відрізків однієї прямої

Тестове завдання
1. Точка М не лежить у площині прямокутника ABCD. Яке взаємне розташування прямих МА і СD ?
А) Перетинаються; Б) паралельні; В) мимобіжні; Г) паралельні або мимобіжні.
2. Пряма а паралельна площині , пряма b належить площині .
Яким може бути взаємне розміщення прямих а і b?
А) Паралельні; Б) перетинаються; В) мимобіжні; Г) мимобіжні або паралельні.
3.Точка М лежить поза площиною трикутника АВС. Точки К, Р, Е і D – середини
відрізків МА, АВ, МС і ВС відповідно. Яке взаємне розміщення прямих
КР і ЕD?
А) Перетинаються; Б) мимобіжні; В) паралельні; Г) мимобіжні або перетинаються.

4. Сторона АВ паралелограма ABCD належить площині , а сторона СD не належить цій площині. Яке взаємне розміщення прямої СD і площини ?
А) пряма СD перетинає площину ; Б) пряма СD паралельна площині ;
В) пряма СD лежить у площині .
5. Пряма а паралельна площині . Скільки площин, паралельних площині
можна провести через пряму а?
А) Одну; Б) дві; И) жодної; Г) безліч.
6. Як розташовані площини і , якщо пряма а перетинає площину
і паралельна площині ?
А) Паралельні; Б) перетинаються; В) збігаються; Г) визначити неможливо.
7. Точка М не належить жодній із паралельних площин і .
Скільки всього існує площин, які проходять через точку М і паралельні площинам
і ?
А) Одна; Б) дві; В) жодної; Г) безліч.

8. Площини і паралельні. Пряма а перетинає площину .
Як розташована пряма а відносно площини ?
А) Паралельна площині; Б) лежить у площині; В) перетинає площину;
Г) визначити неможливо.
9. Основи трапеції паралельні площині . Яке взаємне розміщення площини трапеції і площини ?
А) Перетинаються; Б) паралельні; В) збігаються; Г) визначити неможливо.
10. Площини і паралельні. Площина перетинається з площиною
по прямій а , а з площиною - по прямій b. Яке взаємне розміщення прямих
а і b?
А) Перетинаються; Б) мимобіжні; В) паралельні; Г) визначити неможливо.

Відповіді до тесту
1В , 2Г , 3В , 4Б , 5А ,
6Б , 7А , 8В , 9А , 10В

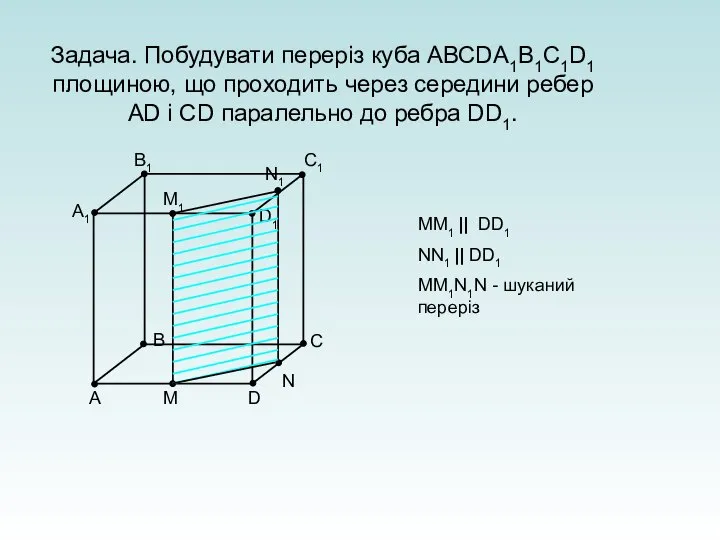
Задача. Побудувати переріз куба АВСDА1В1С1D1 площиною, що проходить через середини ребер АD і СD паралельно до ребра DD1.
ММ1 || DD1
NN1 || DD1
МM1N1N - шуканий переріз
М
N

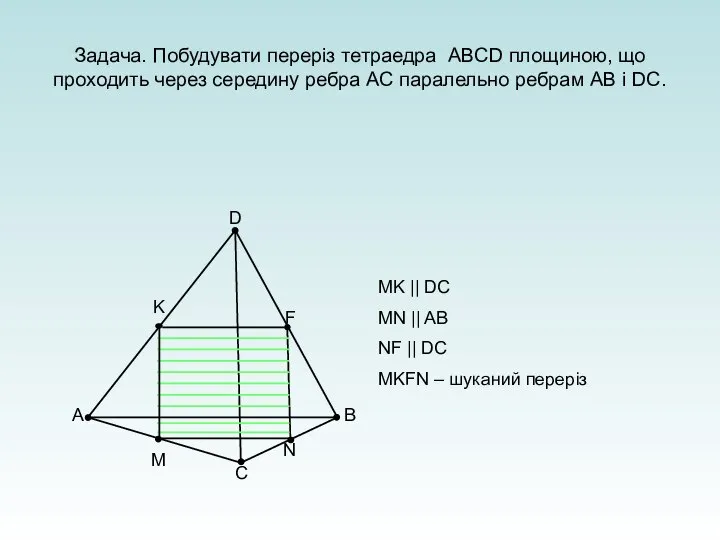
Задача. Побудувати переріз тетраедра ABCD площиною, що проходить через середину ребра АС паралельно ребрам AB і DC.
MK || DC
MN || AB
NF || DC
MKFN – шуканий переріз
D
B
C
A
M

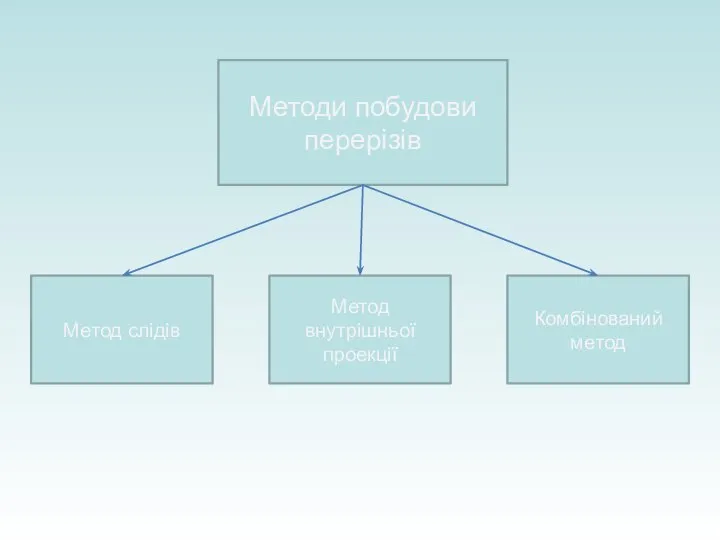
Методи побудови перерізів
Метод слідів
Метод внутрішньої проекції
Комбінований метод

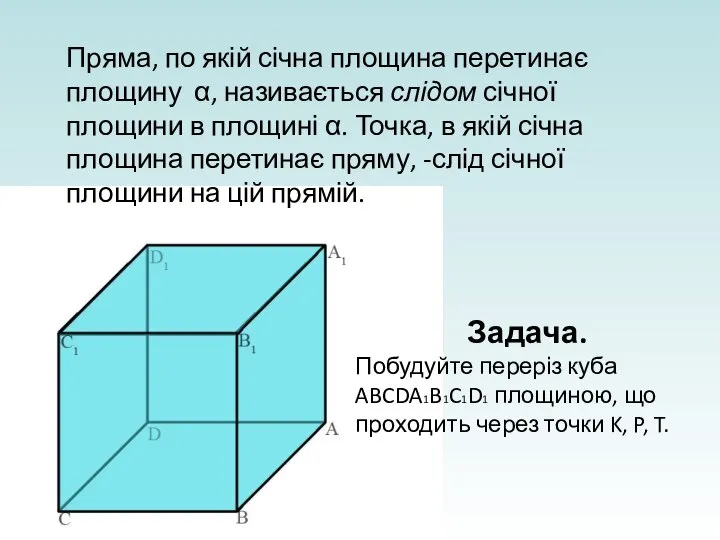
Задача.
Побудуйте переріз куба ABCDA1B1C1D1 площиною, що проходить через точки K, P, T.
Пряма, по якій січна площина перетинає площину α, називається слідом січної площини в площині α. Точка, в якій січна площина перетинає пряму, -слід січної площини на цій прямій.

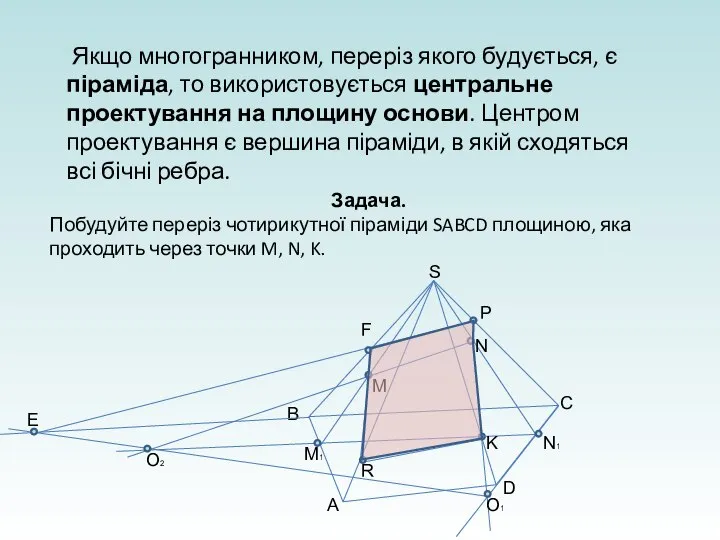
Якщо многогранником, переріз якого будується, є піраміда, то використовується центральне проектування на площину основи. Центром проектування є вершина піраміди, в якій сходяться всі бічні ребра.
Задача.
Побудуйте переріз чотирикутної піраміди SABCD площиною, яка проходить через точки M, N, K.
S
B
D
A
C
K
N
P
O1
O2
E
F
M
N1
M1
R

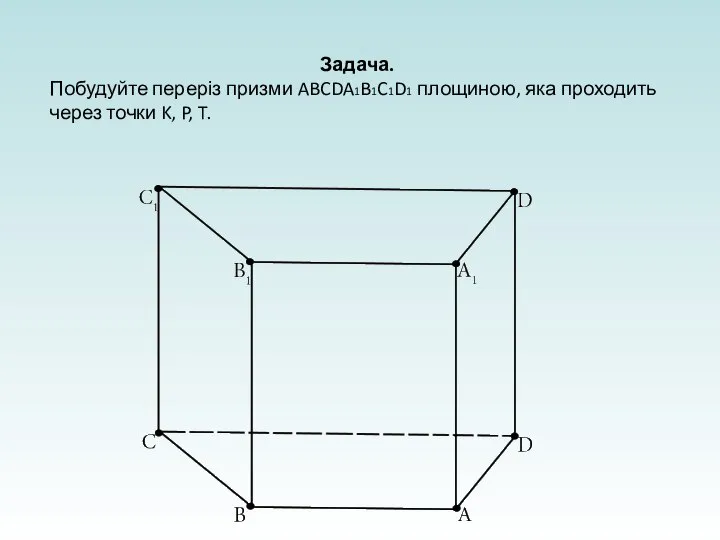
Задача.
Побудуйте переріз призми ABCDA1B1C1D1 площиною, яка проходить через точки K, P, T.

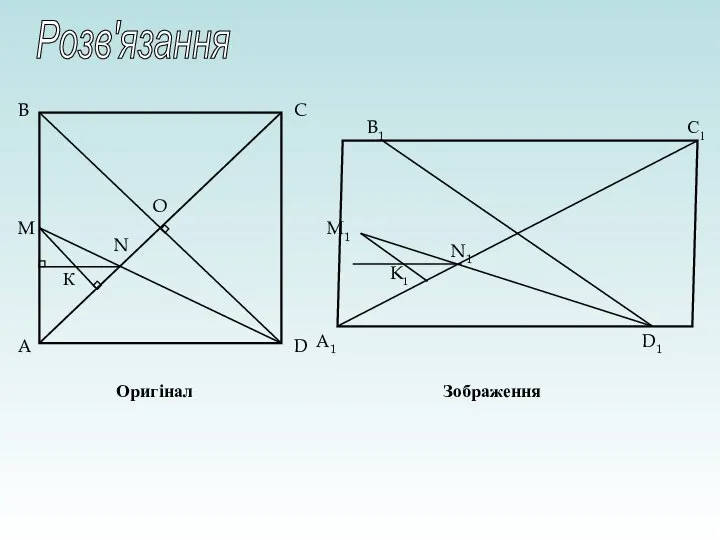
Чотирикутник A1B1C1D1 є зображенням квадрата. Точка М – середина АВ, AC і DM перетинаються у точці N. Побудувати зображення ортоцентра трикутника ANM .
задача

B
A
C
D
M
O
N
К
B1
K1
A1
M1
N1
D1
C1
Оригінал
Зображення
Розв'язання

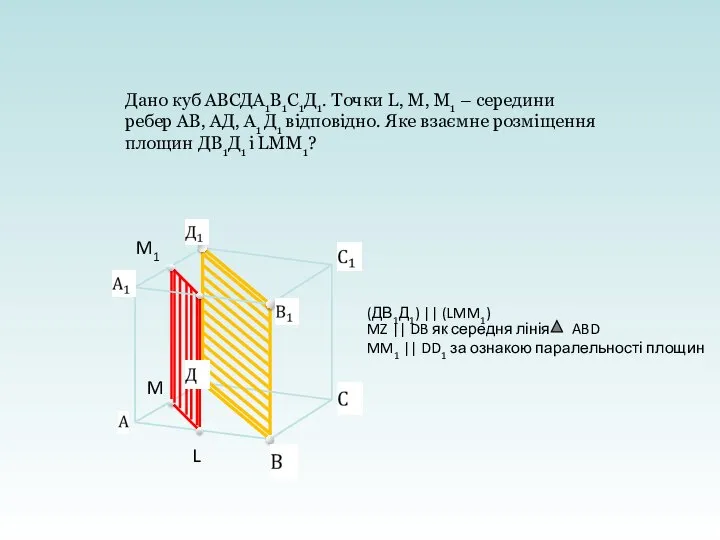
Дано куб АВСДА1В1С1Д1. Точки L, M, M1 – cередини ребер АВ, АД, А1 Д1 відповідно. Яке взаємне розміщення площин ДВ1Д1 і LMM1?
(ДВ1Д1) || (LMM1)
MZ || DB як середня лінія ABD
MM1 || DD1 за ознакою паралельності площин
L
M
M1