Содержание
- 2. Геометрическая прогрессия. Формула n-го члена.
- 3. Определение. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен
- 4. Примеры геометрической прогрессии: а) 2; 4; 8; 16; 32; 64; … q = 2 б) -10;
- 5. ……… Формула n-го члена
- 6. Примеры В геометрической прогрессии = 13, 4 и q=0,2. Найти Решение. По формуле n-ого члена геометрической
- 7. Дано: (bn ) - геометрическая прогрессия b1= 5 q = 3 Найти: b3 ; b5. Решение:
- 8. Найти пятый член геометрической прогрессии: 2; -6… Решение. Зная первый и второй члены геометрической прогрессии, можно
- 9. Дано: (bn ) - геометрическая прогрессия b4= 40 q = 2 Найти: b1. Решение: используя формулу
- 10. Решить в классе (работа по учебнику, стр. 229 № 817 (1 столбец) № 818 № 820
- 12. Скачать презентацию



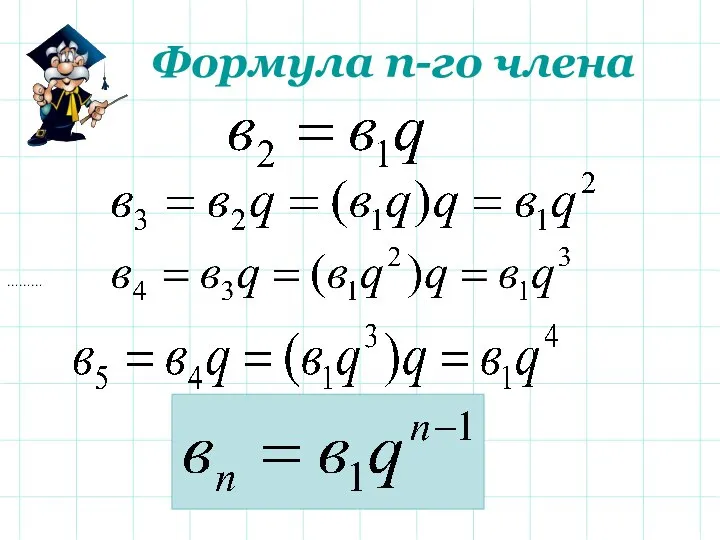





 Устный счёт. 3 класс
Устный счёт. 3 класс Презентация на тему Прибавление числа 4 (1 класс)
Презентация на тему Прибавление числа 4 (1 класс)  Эконометрика, как наука
Эконометрика, как наука Решение задач
Решение задач Презентация на тему Прямая. Отрезок. Или приключения в стране ГЕОМЕТРИИ (1 класс)
Презентация на тему Прямая. Отрезок. Или приключения в стране ГЕОМЕТРИИ (1 класс)  Многогранники. Единица объема. Объем прямоугольного параллелепипеда
Многогранники. Единица объема. Объем прямоугольного параллелепипеда Классическая формула подсчета результатов
Классическая формула подсчета результатов Процедуры и функции работы со строками
Процедуры и функции работы со строками Презентация на тему Решение иррациональных уравнений
Презентация на тему Решение иррациональных уравнений  Текстовые задачи на движение по прямой
Текстовые задачи на движение по прямой Отрезки (Начало)
Отрезки (Начало) Задачи на готовом чертеже. 9 класс
Задачи на готовом чертеже. 9 класс Математика. Роль математики в жизни людей и общества
Математика. Роль математики в жизни людей и общества Несобственные интегралы
Несобственные интегралы Презентация на тему Все действия с десятичными дробями
Презентация на тему Все действия с десятичными дробями  Презентация+ТВ+Законы+распределения
Презентация+ТВ+Законы+распределения График квадратичной функции
График квадратичной функции Геометрические фигуры в жизни и в природе. Проект
Геометрические фигуры в жизни и в природе. Проект Цели урока:
Цели урока: Правила вычисления производных
Правила вычисления производных Variācijas, permutācijas, kombinācijas
Variācijas, permutācijas, kombinācijas Модели и развёртки многогранников
Модели и развёртки многогранников Л 9 Бесконечно большие функции и замечательные пределы
Л 9 Бесконечно большие функции и замечательные пределы Угол между прямой и плоскостью. Теорема о трёх перпендикулярах
Угол между прямой и плоскостью. Теорема о трёх перпендикулярах Графики функций. Задачи с параметрами
Графики функций. Задачи с параметрами Prseyshie_trig_neravenstva
Prseyshie_trig_neravenstva Вписанные и описанные четырехугольники
Вписанные и описанные четырехугольники Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников
Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников