Слайд 2ТЕОРИЯ
Эконометрика изучает связи между явлениями. Связи могут быть полными – функциональными и

неполными – корреляционными. Для функциональной зависимости характерным является то, что изменение признака следствия целиком определяется изменением признаком фактора.
Слайд 3ТЕОРИЯ
Например: площадь круга выражается формулой , S = πR² т.е. площадь круга

изменяется от изменения квадрата ее радиуса.
Корреляционные связи характеризуются тем, что величина признака следствия изменяется под влиянием нескольких факторов. При этом одни факторы оказывают влияние на все единицы изучаемой совокупности, а другие -
Слайд 4ТЕОРИЯ
только на отдельные из них. Корреляционные связи проявляются отчетливо только в большом

числе факторов, т.к. при этом сглаживаются индивидуальные особенности и второстепенные факторы. Например: анализируя производительность труда на предприятии, можно увидеть зависимость от ее уровня энерговооруженности труда.
Слайд 5ТЕОРИЯ
Но производительность труда зависит и от других факторов: от режима работы предприятия,

организации снабжения, квалификации работников и т.д. Поэтому зависимость производительности труда от уровня энерговооруженности труда не может быть полной, а является корреляционной.
Слайд 6ТЕОРИЯ
Для выявления корреляционных зависимостей используют теоретическую формулу связи в виде математического уравнения,

которое называется уравнением регрессии. Регрессия – это зависимость среднего значения величины от другой величины или нескольких величин.
Слайд 7ТЕОРИЯ
Уравнение регрессии может быть описано уравнением линейной связи
Y = a₀ +

a₁x,
гиперболой Y = a₀ + a₁1/x ,
параболой Y = a₀ + a₁x + a₂x².
Если результативный признак (Y) с увеличением факторного признака (X) равномерно возрастает или убывает, то такая зависимость является линейной и выражается уравнением прямой.
Слайд 8ТЕОРИЯ
Найти теоретическое уравнение связи – это значит рассчитать параметры прямой линии методом

наименьших квадратов, который дает систему двух нормальных уравнений.
Слайд 9ТЕОРИЯ
Yx = a₀ + a₁ x
na₀ + a₁∑(x) = ∑(y)
a₀∑(x) + a₁∑(x)

= ∑(xy)
Yx – теоретическое значение результативного признака.
Y – индивидуальное значение результативного признака.
Слайд 10ТЕОРИЯ
n– число показателей.
X - индивидуальное значение результативного признака.
a₀,a₁ – параметры (коэффициенты) уравнения

регрессии.
Слайд 11ТЕОРИЯ
Теоретическое уравнение выражает функциональную зависимость (Y) от (X). Это возможно допустить, если

прочие факторы, влияющие на (Y) не оказывают в данном случае существенного влияния.
Слайд 12ТЕОРИЯ
Это бывает, когда корреляционная зависимость между (Y) и (X) высокая. В этом

случае параметр (a₁) при (X) в уравнении регрессии приобретает большое практическое значение. Этот параметр, который называется коэффициентом регрессии,
характеризует, в какой мере увеличивается (Y ) , с ростом величины (X).
Слайд 13ЗАДАЧА
Имеются выборочные данные по однородным предприятиям: энерговооруженность труда одного рабочего (квт /час)

и выпуск готовой продукции (шт).
ОПРЕДЕЛИТЬ:
1. Факторные и результативные признаки.
2. Провести исследование взаимосвязи энерговооруженности и выпуска готовой продукции.
Слайд 14ЗАДАЧА
3. Построить уравнение регрессии и вычислить коэффициент регрессии.
4. Построить графики практической и

теоретической линии регрессии.
5. Определить форму связи и измерить тесноту связи.
6. Провести оценку адекватности.
Слайд 15РЕШЕНИЕ
1. (Х) – факторным признаком является энерговооруженность.
(Y)– результативным признаком является выпуск готовой

продукции.
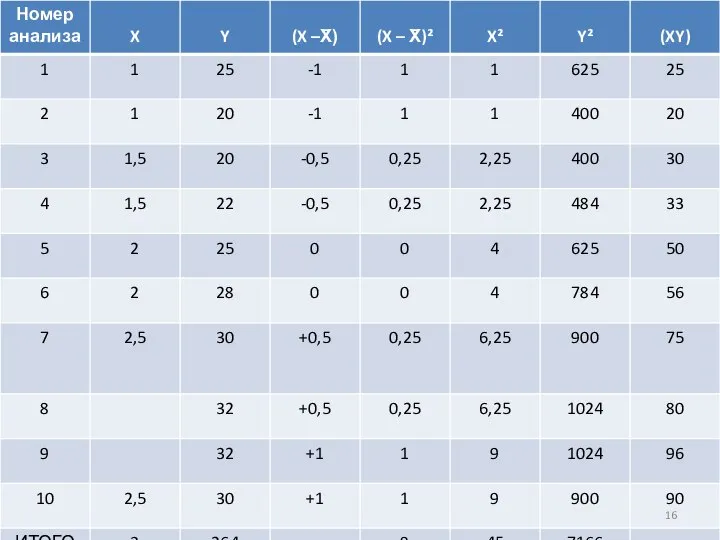
2. Исходные данные поместим в следующую таблицу.
Слайд 17РЕШЕНИЕ
3. Первичная информация проверяется на однородность по признаку-фактору с помощью коэффициента вариации

Слайд 18РЕШЕНИЕ
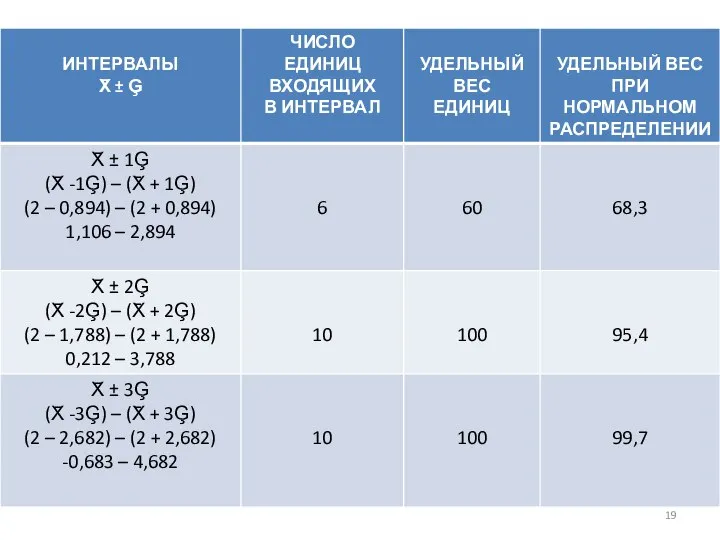
4. Проверка первичной информации на нормальность распределения с помощью правила «трех сигм».

Сущность правила заключается в том, что в интервал «трех сигм» должны попасть факторные признаки. Те показатели, которые больше или меньше интервала «трех сигм», удаляются из таблицы.
Слайд 20РЕШЕНИЕ
5. Исключить из первичной информации резко выделяющиеся единицы, которые по признаку-фактору не

попадают в интервал «трех сигм».
Вывод: Резко выделяющихся единиц в первичной информации нет.
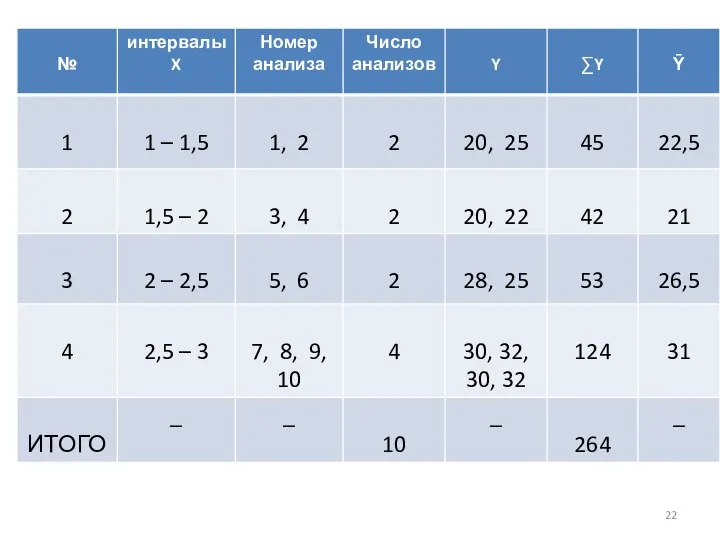
Слайд 216. Для установления факта наличия связи производится аналитическая группировка по признаку-фактору. Построить

интервальный ряд распределения.
При этом формула для определения величины интервала имеет следующий вид:
Слайд 23РЕШЕНИЕ
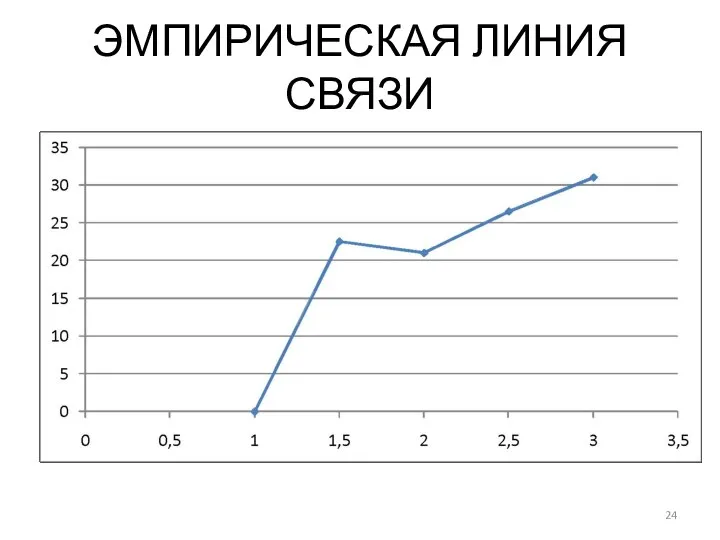
7. Построить эмпирическую линию связи. По оси абсцисс откладываются значения интервалов факторного

признака – (X) . По оси ординат откладываются значения средней величины результативного признак – (Ȳ).
Слайд 258. Для измерения степени тесноты связи используется линейный коэффициент связи:

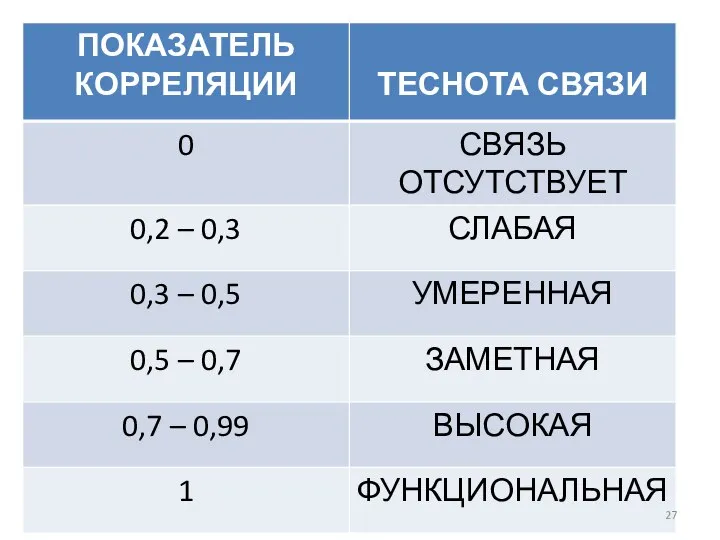
Слайд 26РЕШЕНИЕ
Полученное значение линейного коэффициента корреляции необходимо сравнить с табличными данными.

Слайд 28РЕШЕНИЕ
Т.о. связь высокая. r = 0,86, а интервал связи (0,7 – 0,99).
9.

Предположим, что между энерговооруженности труда и выпуском готовой продукции существует линейная корреляционная связь которую можно выразить уравнением прямой.
Для этого составим новую таблицу.
Слайд 30Вычислим параметры прямой с помощью системы двух нормальных уравнений:
Yx = a₀ +

a₁X
na₀ + a₁Σ(X) = Σ(Y)
a₀∑(X) + a₁∑(X²) = ∑(XY)
10a₀ + 20a₁ = 264
20a₀ + 45a₁ = 555
10a₀ + 20a₁ = 264 х { (-2)}
20a₀ + 45a₁ = 555
Слайд 31РЕШЕНИЕ
-20a₀ – 40a₁ = -528
+20a₀ + 45a₁ = 555
5a₁ = 27
a₁

= 5,4
a₀ = 15,6
Слайд 32РЕШЕНИЕ
Конечное уравнение следующее.
Yx = 15,6 + 5,4(X)
В уравнении регрессии коэффициент a₁

показывает, что с увеличением энерговооруженности труда одного рабочего на 1 (квт/час) выпуск готовой продукции возрастает на 5,4 шт.
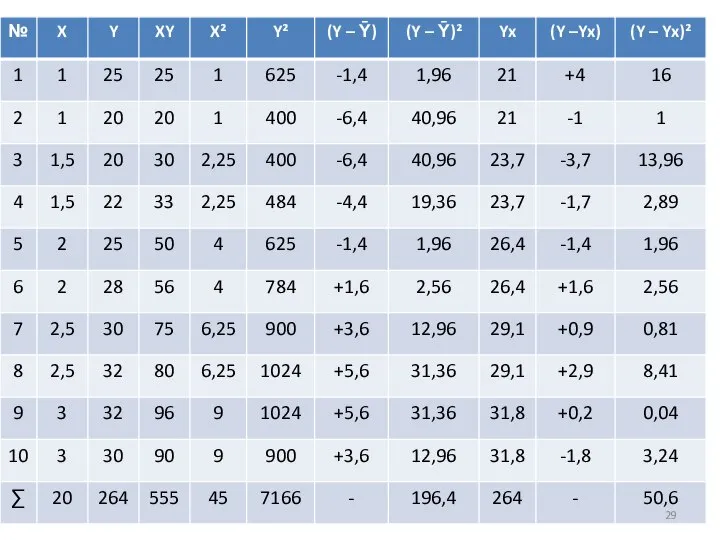
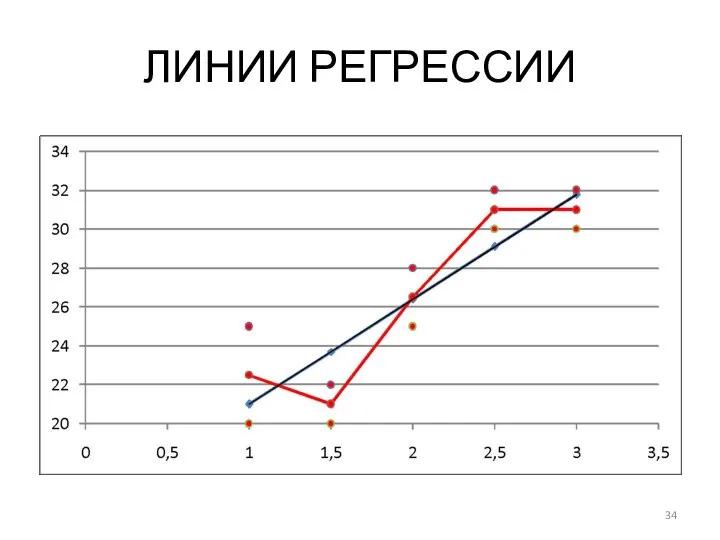
Слайд 33РЕШЕНИЕ
Построим графики практической и теоретической линии регрессии. По оси абсцисс отложим значения

факторного признака (x) , по оси ординат (Yx) и (Y). Чтобы определить (Yx) в уравнение регрессии подставить значения (x) и занести в таблицу.
Слайд 35ИЗМЕРИТЬ ТЕСНОТУ СВЯЗИ
10. Одним из важнейших этапов исследования является измерение тесноты связи.

Для этого применяют линейный коэффициент корреляции (r) и индекс корреляции (R). Индекс корреляции применяется для измерения тесноты связи между признаками при любой форме связи, как линейной, так и нелинейной.
Слайд 36Но его можно вычислять только после того, как определена форма связи и

вычислена теоретическая линия регрессии.
Слайд 37Индекс корреляции измеряется от 0 до 1. Чем ближе индекс к 1,

тем теснее связь между признаками. Частным случаем индекса корреляции является коэффициент корреляции, который применяется только при линейной форме связи. В отличии от индекса корреляции линейный коэффициент корреляции показывает не только тесноту связи, но и направление связи (прямая или обратная) и измеряется от -1 до +1.
Слайд 38ВЫВОД
Все показатели тесноты корреляционной связи показывают тесную связь между производительностью труда и

энерговооруженностью труда. Т.к. R=r=0,86 то можно сделать заключение, что гипотеза о линейной форме связи подтверждена.
Слайд 39АДЕКВАТНОСТЬ МОДЕЛИ
Проведем оценку адекватности регрессионной модели с помощью критерия Фишера.

Слайд 40ВЫВОД
Табличное значение критерия Фишера равно (Fт = 20,20). Эмпирическое значение критерия Фишера

(Fэ = 23,048)сравниваем с табличным.
Если Fэ < Fт, то уравнение регрессии можно признать неадекватным.
Если Fэ > Fт, то уравнение регрессии признается значимым. (23,048 > 20,20)
Т.о. данная модель является адекватной.
































 Решение уравнений. 6 класс
Решение уравнений. 6 класс Теорема Пифагора. Решение задач. Урок для 8 класса
Теорема Пифагора. Решение задач. Урок для 8 класса Тригонометрические функции. Формулы двойного угла
Тригонометрические функции. Формулы двойного угла Графики функций у = ах2+n и y= a(x – m)2
Графики функций у = ах2+n и y= a(x – m)2 Многогранники. Призма
Многогранники. Призма Показательная функция
Показательная функция Графы. Способы задания графов. Степени вершин
Графы. Способы задания графов. Степени вершин Элементы линейной алгебры и геометрии выпуклых множеств
Элементы линейной алгебры и геометрии выпуклых множеств Таблица умножения на 2
Таблица умножения на 2 Правильные многоугольники
Правильные многоугольники Вычитание дробных чисел. 5 класс
Вычитание дробных чисел. 5 класс Презентация на тему Алгебраические уравнения произвольных степеней 10 класс
Презентация на тему Алгебраические уравнения произвольных степеней 10 класс  Периметр восьмиугольника
Периметр восьмиугольника Математичний диктант. Паралелограм
Математичний диктант. Паралелограм Векторное кодирование графической информации
Векторное кодирование графической информации Окружность
Окружность Четырехугольник . Прямоугольник. Квадрат
Четырехугольник . Прямоугольник. Квадрат Параллелепипед
Параллелепипед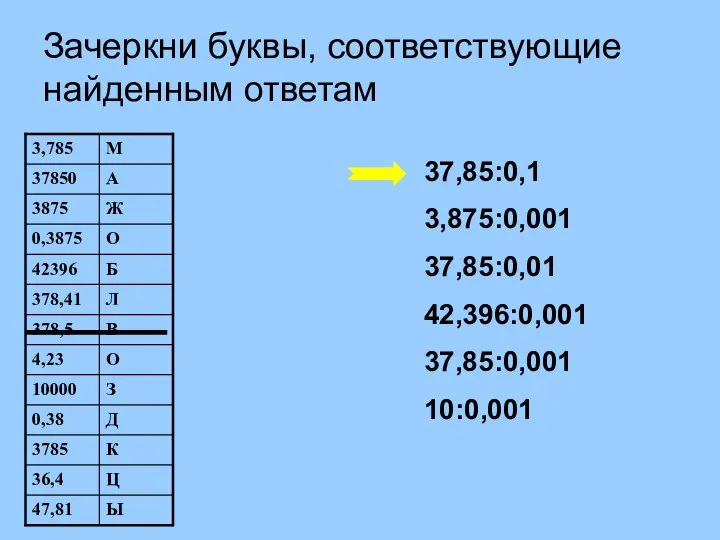 Устная работа (1). Зачеркни буквы, соответствующие найденным ответам
Устная работа (1). Зачеркни буквы, соответствующие найденным ответам Интерактивный тренажёр Реши уравнения
Интерактивный тренажёр Реши уравнения Элементы нелинейного функционального анализа. Гладкие многообразия
Элементы нелинейного функционального анализа. Гладкие многообразия Моделирование – способ, процесс замещения оригинала его аналогом (моделью)
Моделирование – способ, процесс замещения оригинала его аналогом (моделью) Задачи на проценты
Задачи на проценты Живая планета!
Живая планета! Квадратные уравнения
Квадратные уравнения Устный счет в пределах 10. Состав чисел 7, 8
Устный счет в пределах 10. Состав чисел 7, 8 Моделирование на графах
Моделирование на графах Стороны треугольника пропорциональны синусам противолежащих углов
Стороны треугольника пропорциональны синусам противолежащих углов