Слайд 2
1. Бесконечно большие функции, их связь с бесконечно малыми функциями.
Определение 1.

Функция f(x) называется бесконечно большой в точке x0, если для любого N существует такое число δ>0, что для любого х, удовлетворяющего условию |x–x0|<δ следует |f(x)|>N.
Слайд 3
Лекция № 9
Графики бесконечно больших функций
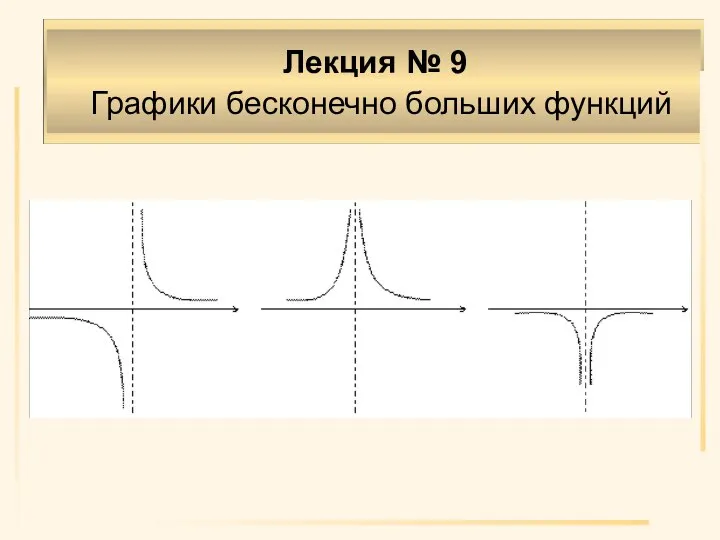
Слайд 4
Теорема 1.
Если f(x) – бесконечно большая величина, то – бесконечно

малая величина; если f(x) – бесконечно малая величина и f(x)≠0, то – бесконечно большая величина.
Слайд 5
Пример 1.
f(x)=x2 – бесконечно малая величина при х→0;
– бесконечно

большая величина при х→0.
Слайд 6
Свойства бесконечно больших функций
Свойство 1. Сумма конечного числа бесконечно больших функций

при х→х0 тоже бесконечно большая функция при х→х0.
Слайд 7
Свойство 2.
Произведение конечного числа бесконечно больших функций при х→х0 тоже бесконечно

большая функция при х→х0.
Слайд 8
Свойство 3.
Произведение бесконечно большой функции при х→х0 на функцию, имеющую

предел, отличный от нуля, а следовательно, и произведения бесконечно большой функции на постоянную, не равную нулю, являются бесконечно большой функцией при х→х0.
Слайд 9
2. Замечательные пределы
Первый замечательный предел

Слайд 10
Геометрическая интерпретация
∠АОВ = х

Слайд 11
Доказательство замечательного предела
sinx < x < tgx
при 0 < x

< , sinx >0
Слайд 12
Следствия из первого замечательного предела

Слайд 15
Следствия из второго замечательного предела

Слайд 16
При α(х)→0 справедливы следующие соотношения эквивалентности
3. Сравнение бесконечно малых функций.
Эквивалентные

бесконечно малые функции.
Слайд 19Предел называют
неопределенностью типа
4. Раскрытие неопределенностей

Слайд 21
Предел называют
неопределенностью типа

Слайд 22
Предел называют
неопределенностью типа 0 ⋅ ∞.

Слайд 23
Предел называют
неопределенностью типа ∞–∞.

Слайд 245. Показательно-степенные неопределенности
Показательно-степенные неопределенности 00, ∞0, 1∞ сводятся к неопределенности ∞⋅0 следующим

образом: .























 Показательные уравнения
Показательные уравнения Задача по математике (1 класс)
Задача по математике (1 класс) Способы быстрого счета
Способы быстрого счета Векторы. Задания
Векторы. Задания Найдите наименьшее (наибольшее) значение функции на промежутке
Найдите наименьшее (наибольшее) значение функции на промежутке Математические методы. Пример построения математической модели. Задача о минимизации
Математические методы. Пример построения математической модели. Задача о минимизации Математические игры и задачи
Математические игры и задачи Страна Математика
Страна Математика Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов
Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов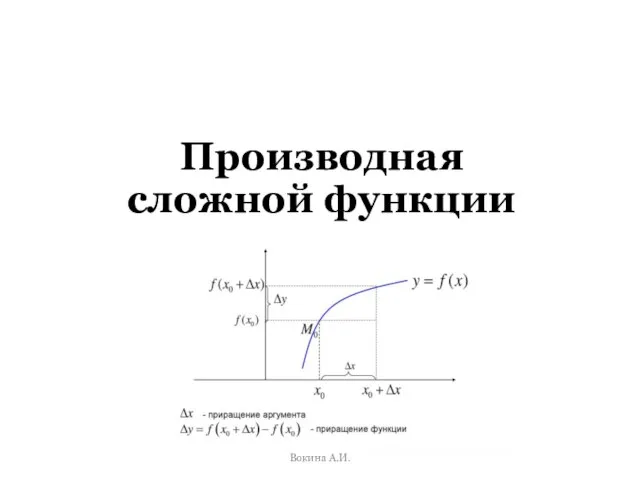 Производная сложной функции
Производная сложной функции Крапки від 0 до 20
Крапки від 0 до 20 Таблица истинности
Таблица истинности Сумма п-первых членов арифметической прогрессии
Сумма п-первых членов арифметической прогрессии Число 10
Число 10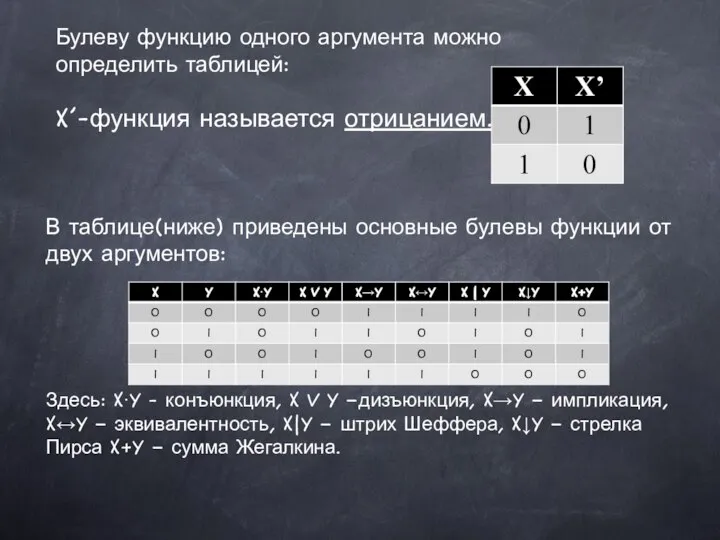 Булевы функции
Булевы функции Техника времен Великой Отечественной войны. Решение тематических задач
Техника времен Великой Отечественной войны. Решение тематических задач Трапеция. Основание
Трапеция. Основание Задачи на клетке
Задачи на клетке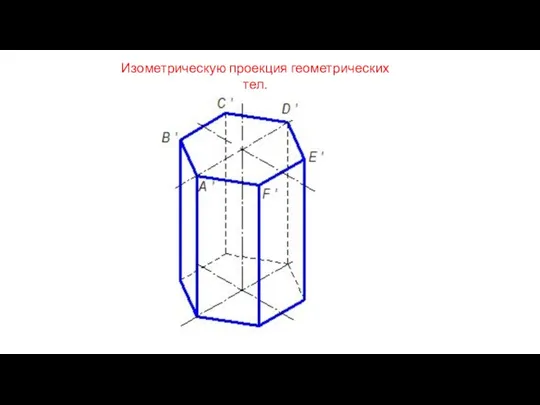 Шестигранная призма в изометрии
Шестигранная призма в изометрии Презентация на тему ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ
Презентация на тему ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ  Подготовка к ЕГЭ по математике. Задание 18 (задачи по планиметрии)
Подготовка к ЕГЭ по математике. Задание 18 (задачи по планиметрии) Игра 3
Игра 3 Xüsusi törəməli diferensial tənliklərin həlli metodları
Xüsusi törəməli diferensial tənliklərin həlli metodları Дополни до 10
Дополни до 10 Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Следствия из теорем синусов и косинусов
Следствия из теорем синусов и косинусов аксіоми стереометрії
аксіоми стереометрії Презентация на тему Приемы устного счета
Презентация на тему Приемы устного счета