Содержание
- 2. Цели обучения: 7.1.1.31 знать определение геометрического места точек
- 3. Геометрическое место – термин, применявшийся в старой литературе по геометрии и до сих пор применяющийся в
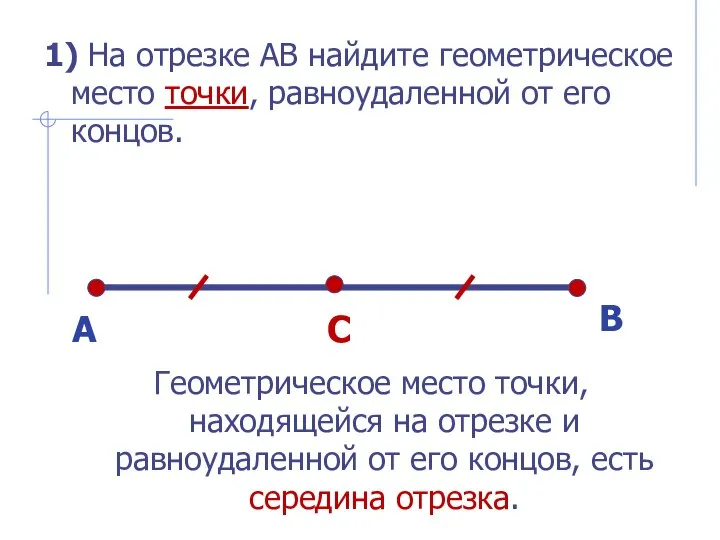
- 4. 1) На отрезке АВ найдите геометрическое место точки, равноудаленной от его концов. Геометрическое место точки, находящейся
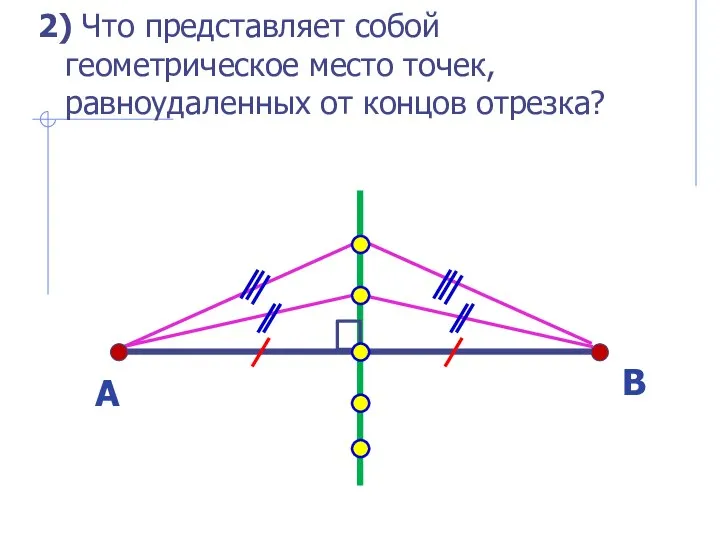
- 5. 2) Что представляет собой геометрическое место точек, равноудаленных от концов отрезка?
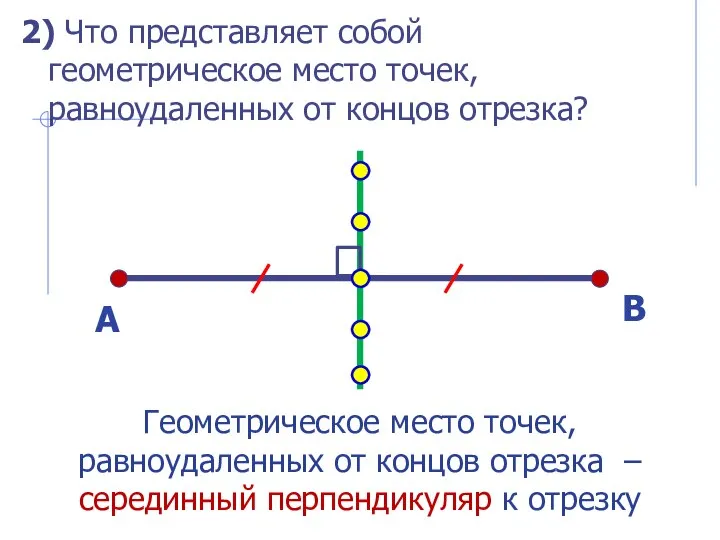
- 6. 2) Что представляет собой геометрическое место точек, равноудаленных от концов отрезка? Геометрическое место точек, равноудаленных от
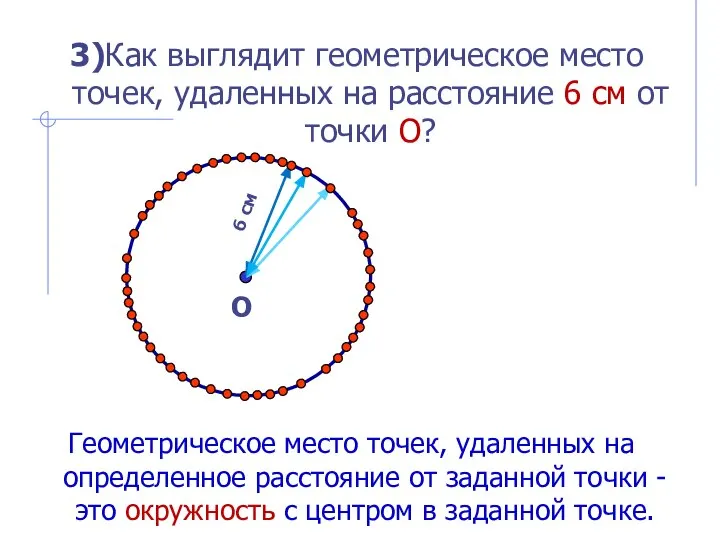
- 7. О 6 см 3)Как выглядит геометрическое место точек, удаленных на расстояние 6 см от точки О?
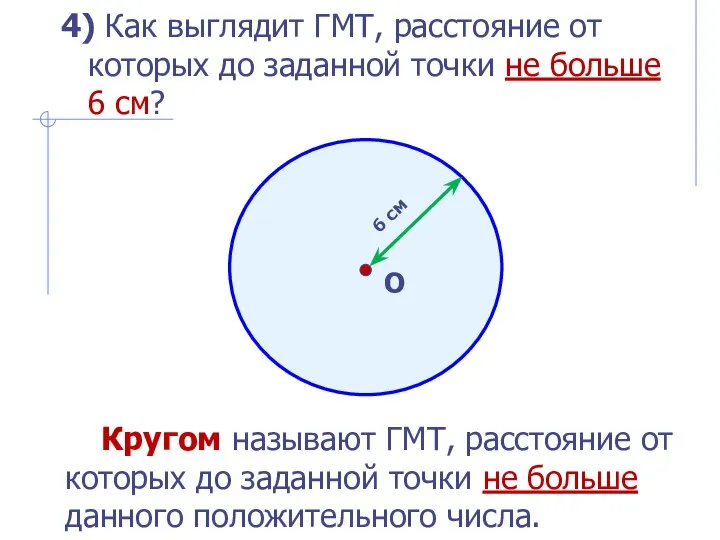
- 8. 6 см О 4) Как выглядит ГМТ, расстояние от которых до заданной точки не больше 6
- 9. Задачи на нахождение ГМТ Решение задачи на поиск ГМТ должно содержать доказательство того, что все точки
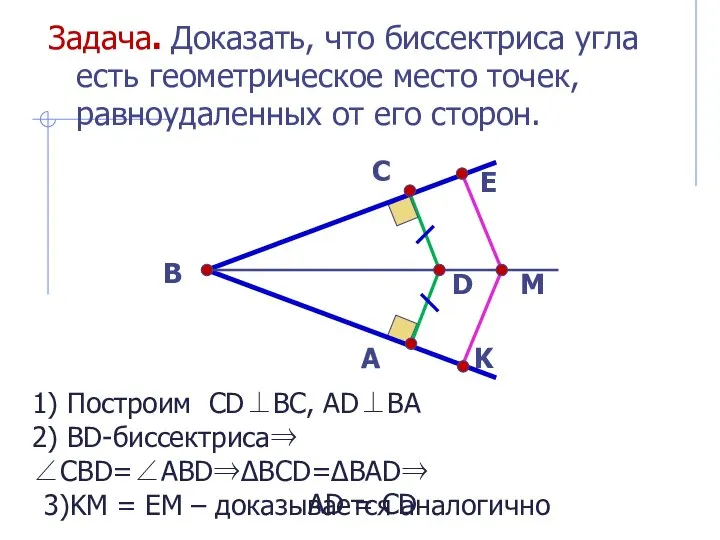
- 10. Задача. Доказать, что биссектриса угла есть геометрическое место точек, равноудаленных от его сторон. 1) Построим CD⊥BC,
- 11. ЗАПОМНИТЕ Самые известные примеры ГМТ. Геометрическое место точек, равноудаленных от концов отрезка, — серединный перпендикуляр к
- 12. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ Желаю успеха!
- 13. Задание 1. Ответьте на вопросы. 1) Что, на ваш взгляд, является геометрическим местом точек, равноудаленным от
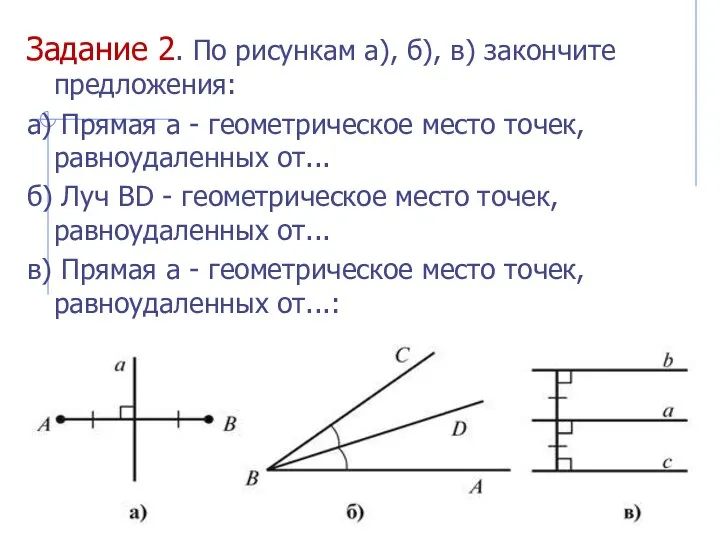
- 14. Задание 2. По рисункам а), б), в) закончите предложения: а) Прямая a - геометрическое место точек,
- 15. Задание 3. Можно ли круг радиуса 5 см считать геометрическим местом точек, удаленных от центра этого
- 16. Задание 4. Отрезок AB равен 4 см. Можно ли считать срединный перпендикуляр этого отрезка геометрическим местом
- 18. Скачать презентацию








 Координаты вектора
Координаты вектора Устный счет
Устный счет Логарифмические уравнения
Логарифмические уравнения Графики функций. Задания
Графики функций. Задания Многогранники. Виды многогранников
Многогранники. Виды многогранников Сложение и умножение вероятностей
Сложение и умножение вероятностей Работа в тетради
Работа в тетради Решение задач на тему Энергосбережение
Решение задач на тему Энергосбережение Линейная функция
Линейная функция Презентация на тему Окружность. Круг.
Презентация на тему Окружность. Круг.  Деление отрезка на равные части с помощью циркуля и линейки
Деление отрезка на равные части с помощью циркуля и линейки Подобные треугольники
Подобные треугольники Сходимость несобственных интегралов первого рода от функций произвольного знака. Признак Больцано Коши. Лекция 2-13
Сходимость несобственных интегралов первого рода от функций произвольного знака. Признак Больцано Коши. Лекция 2-13 Площадь многоугольника. Свойства площадей
Площадь многоугольника. Свойства площадей Визуализация операций над эллиптическими кривыми
Визуализация операций над эллиптическими кривыми Сложение и вычитание дробей
Сложение и вычитание дробей Введение в биоинформатику. Лекция 9
Введение в биоинформатику. Лекция 9 Замена переменных в определенном интеграле. Лекция 4
Замена переменных в определенном интеграле. Лекция 4 Математика вокруг нас (4 класс)
Математика вокруг нас (4 класс) Презентация на тему Использование игровых моментов при повторении на уроках математики в 5-ых классах
Презентация на тему Использование игровых моментов при повторении на уроках математики в 5-ых классах  Решение иррациональных уравнений. Разные методы
Решение иррациональных уравнений. Разные методы Qeyri stasionar qaz dinamikasi. Tənliyinin riyazi modelinin. Qurulmasi
Qeyri stasionar qaz dinamikasi. Tənliyinin riyazi modelinin. Qurulmasi Устные вычисления. Сравнение текстов задач
Устные вычисления. Сравнение текстов задач Системы линейных уравнений
Системы линейных уравнений Презентация на тему Объем прямой призмы
Презентация на тему Объем прямой призмы  Касательная к окружности. 8 класс
Касательная к окружности. 8 класс Сложение и вычитание алгебраических дробей с разными знаменателями
Сложение и вычитание алгебраических дробей с разными знаменателями Формулы сложения
Формулы сложения