Содержание
- 2. Эйлеровы графы Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу,
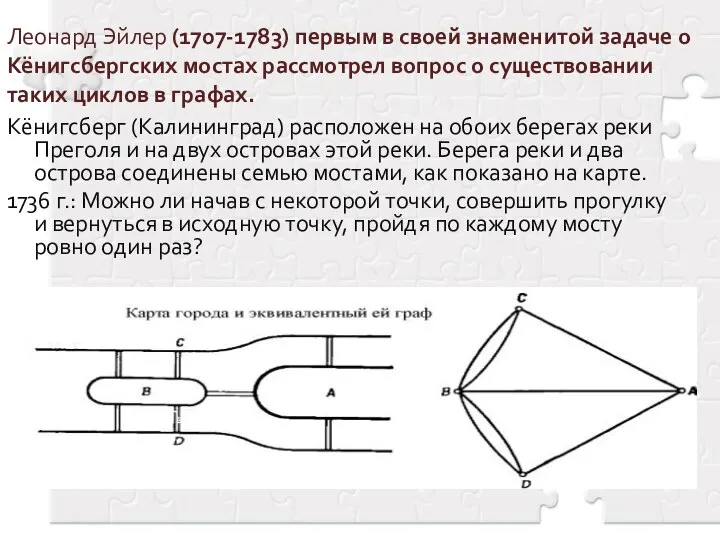
- 3. Леонард Эйлер (1707-1783) первым в своей знаменитой задаче о Кёнигсбергских мостах рассмотрел вопрос о существовании таких
- 4. Теорема Если неориентированный граф G связен и в нем более одной вершины, то следующие утверждения эквивалентны:
- 5. попав в очередную отличную от v1 вершину, будем иметь в распоряжении еще непройденное ребро. Добавим его
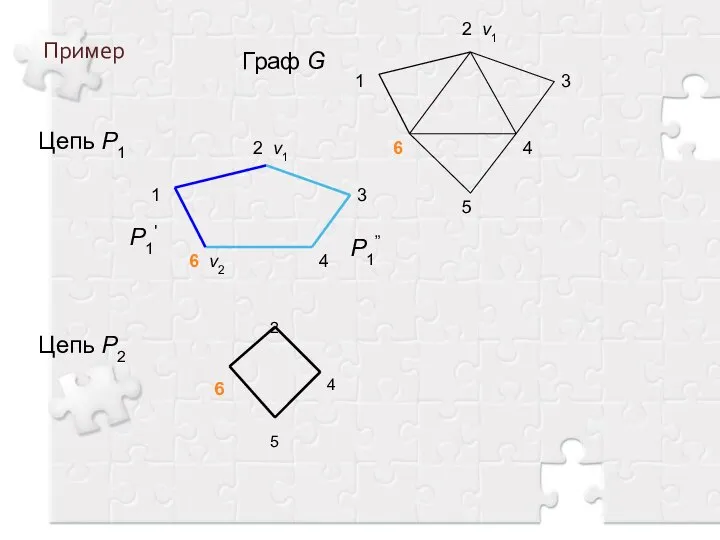
- 6. Пример Граф G Цепь P1 P1” Цепь P2
- 7. Алгоритмы поиска эйлерова цикла Алгоритм Флёри ( сложность O(n*(n+m)) Требуется занумеровать ребра графа числами 1, 2,
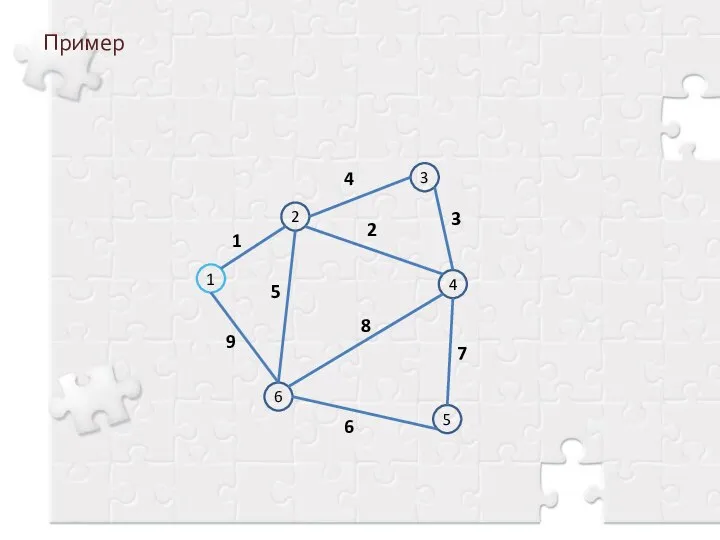
- 8. Пример 1 2 4 3 6 5 1 2 3 4 5 6 7 8 9
- 9. Алгоритм поиска эйлерового цикла (О(n+m)) Начиная с произвольной вершины, строим путь, удаляя ребра и запоминая вершины
- 10. Алгоритм Вход: эйлеров граф G(V, E), заданный списками смежности (Γ[v] — список вершин смежных с вершиной
- 11. Рекурсивная реализация void cycle_search(u) { for (берем любое непройденное ребро (u,v)) { (u,v) – отметить и
- 12. Теорема Граф G 2-раскрашиваемый ⬄ G – эйлеров
- 14. Скачать презентацию





![Алгоритм Вход: эйлеров граф G(V, E), заданный списками смежности (Γ[v] — список](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1105729/slide-9.jpg)


 Квадратные уравнения. Устная разминка
Квадратные уравнения. Устная разминка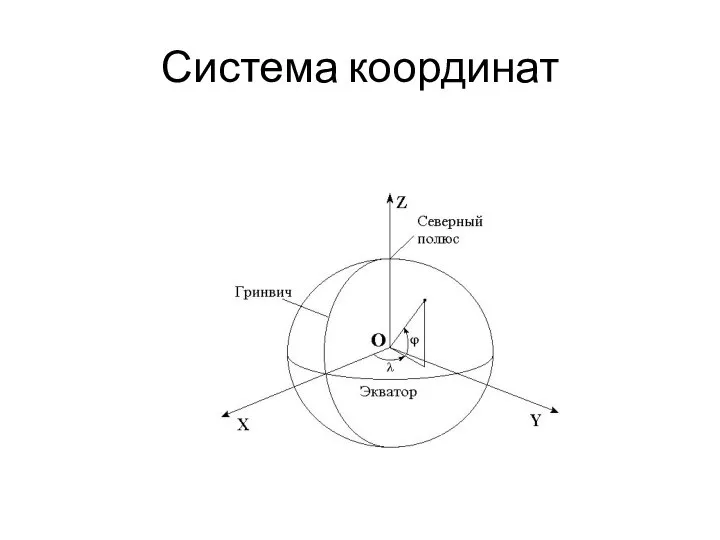 Система координат. Географические координаты
Система координат. Географические координаты Компетентностно-ориентированные задания, как средство формирования ключевых компетенций учащихся
Компетентностно-ориентированные задания, как средство формирования ключевых компетенций учащихся Математичний квест. Дорогою до школи
Математичний квест. Дорогою до школи Пирамиды. Правильная пирамида
Пирамиды. Правильная пирамида Вычисление углов между прямыми и плоскостями
Вычисление углов между прямыми и плоскостями О треугольниках
О треугольниках Элементы теории вероятностей
Элементы теории вероятностей Площадь. Площадь прямоугольника. 5 класс
Площадь. Площадь прямоугольника. 5 класс ANX.ADJ.DSM.5
ANX.ADJ.DSM.5 Цифра и число 3
Цифра и число 3 Презентация на тему Ромб
Презентация на тему Ромб  Морское путешествие
Морское путешествие Неопределённый интеграл
Неопределённый интеграл Модели и развёртки многогранников
Модели и развёртки многогранников Задачи
Задачи Алгебра логики
Алгебра логики Графы
Графы Критерий Манна-Уитни
Критерий Манна-Уитни Линейная функция, ее график и свойства (занятие 2)
Линейная функция, ее график и свойства (занятие 2) Загадки и шарады
Загадки и шарады Презентация на тему Переменная
Презентация на тему Переменная  Динамическое программирование
Динамическое программирование Исследование функции с помощью производной
Исследование функции с помощью производной Итоги пробного ОГЭ от 27.02.2021. Разбор варианта №1
Итоги пробного ОГЭ от 27.02.2021. Разбор варианта №1 Комбинаторная задача с монетами
Комбинаторная задача с монетами Анализ и синтез как методы научного познания, их применение при обучении математике
Анализ и синтез как методы научного познания, их применение при обучении математике Технология подготовки учащихся к овладению функционально-графическими методами решения задач с параметрами. (Занятие №3)
Технология подготовки учащихся к овладению функционально-графическими методами решения задач с параметрами. (Занятие №3)